平衡树splay浅谈
有关前置知识例如BST旋转,可查看之前的treap博客。
简单一谈:
BST:
二叉搜索树,对于任意一结点满足左子树<根节点<右子树。
旋转:
用动画说明,生动形象。分别是左旋右旋: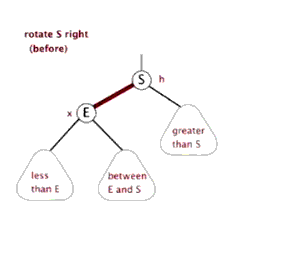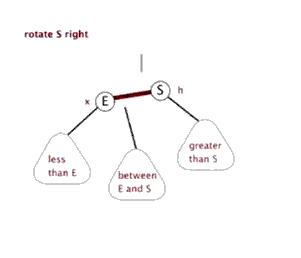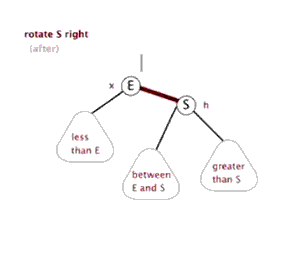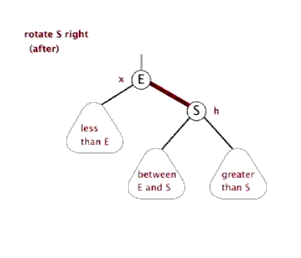
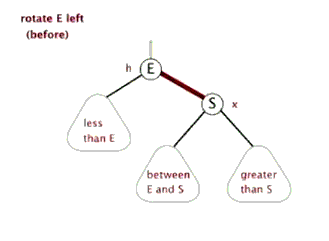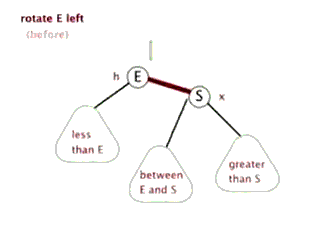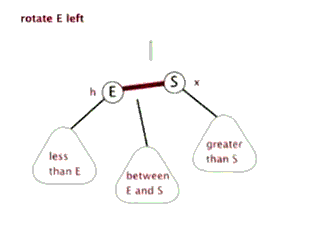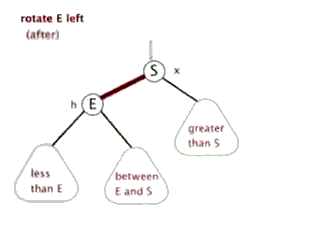
splay:
基本原理:
因为一棵二叉搜索树可能会出现深浅不一,树的重心偏移的问题,导致搜索时间的不稳定,甚至会被毒瘤出题人给卡掉。
为了解决这一问题,splay的操作是:随时把一个结点旋转到根节点,来均摊树的深度。
关于均摊来降低时间复杂度的原理,蒟蒻也说不清楚。建议网上查找一下dalao们的证明博客OvO。
我们定义rotate操作表示将当前结点往上提一层。(下文简称为“提”)根据定义可知,这个操作包含了当前节点为左或右结点的情况。我们
void rotate(int x)
{ int f=fa[x],ff=fa[f],w=get(x);//ff表示爷爷结点,f表示父亲节点,w表示判断x为左节点还是右结点的结果。
son[f][w]=son[x][w^1];//正常的旋转操作 fa[son[f][w]]=f; son[x][w^1]=f; fa[f]=x; fa[x]=ff; if(ff)
{//父节点不是根节点(根节点的父节点为0) son[ff][son[ff][1]==f]=x; } update(f);//修改结点数值 update(x); }
在这之中,左右节点无非就是0和1,^1操作保证了无论当前节点是左结点还是右结点,都能够取到自己的对立结点(兄弟结点)。
get表示判断当前节点为父亲的左儿子还是右儿子。
int get(int x)
{ return son[fa[x]][1]==x; }
update修改操作:
void update(int x)
{ if(x!=0)
{如果x不是根节点 siz[x]=cnt[x]; if(son[x][0]) siz[x]+=siz[son[x][0]]; if(son[x][1]) siz[x]+=siz[son[x][1]]; } }
以上部分为一次旋转的操作单元。对于要把当前结点提到根节点这一总目的,我们只需要边循环边判断即可。
对于一种特殊情况:当前结点,父亲,爷爷在一条直线上,也就是都是曾爷爷的左儿子或者右儿子,单纯对自己结点往上提两次,显然这样操作会不利于树中间(直观看上去的中间)的结点的分布,进而影响树的平衡,违背了我们splay的初衷。
怎么做呢》我们只要先提一下父亲结点,然后在提当前结点就可以了。
void splay(int x) { for(int f;f=fa[x];rotate(x))//传说中的循环上提
{ if(fa[f])
{ rotate(get(x)==get(f)?f:x);判断三点一线情况来决定上提对象。 } } }
splay的灵魂就此结束。
插入操作:
void insect(int v){ if(sz==0)
{ sz++; son[1][1]=son[1][0]=fa[1]=0; siz[1]=cnt[1]=1; root=1; key[1]=v; return; } int now=root,f=0; while(1)
{ if(key[now]==v)
{ cnt[now]++; update(now); update(f); splay(now); break; } f=now; now=son[now][v>key[now]];//依照节点值查找位置,如果大于当前值v>key[now]=1,则在右子树范围内,反之亦然 if(now==0)
{//树中无这个值,查找到树的底端,新建一个子节点 sz++;//新节点编号 son[sz][1]=son[sz][0]=0;//新节点初始化 fa[sz]=f; siz[sz]=cnt[sz]=1; son[f][v>key[now]]=sz;//判断新节点是左节点还是右节点并更新父节点 key[sz]=v; update(f);//更新数量 splay(sz);//旋转到根节点 break; } } }
查找排名:
int find(int v)
{ int ans=0,now=root;//ans记录已经有多少比它小的点,now表示正在寻找的节点的编号 while(1){ if(v<key[now]){//如果当前节点的值大于v,那么当前节点的左子树不完全小于v,继续向当前节点的左子树寻找 now=son[now][0]; } else{//当前节点的左子树上的值必然全部小于v ans+=(son[now][0]!=0?siz[son[now][0]]:0);//如果有左子树则直接加上左子树的数量 if(v==key[now]){//如果当前节点的值等于v,则右子树上不可能有比它小的数,所有比它小的数已经找完 splay(now);//下一次可能的操作 return ans+1;//有1个数比它小那么它应该是第2,以此类推,要+1 } ans+=cnt[now];//key[now]<v的情况,除了它的左儿子还要加上它自身的数量 now=son[now][1];//右子树中可能存在比v小的值,所以在右子树中继续寻找 } } }
查找排名为x的元素是:
int findx(int x)
{ int now=root;//当前节点 while(1){ if(son[now][0]!=0&&siz[son[now][0]]>=x){//如果左子树的数量大于x,就是说第x个是在左子树上(前提是有左子树) now=son[now][0];//在左子树上接着搜索 } else{//第x个在以当前节点为顶点的树中 int less=(son[now][0]!=0?siz[son[now][0]]:0)+cnt[now];//左子树的数量(可能没有)+当前节点的值的数量 if(x<=less)//由于之前判断过是否在左子树上,并且在之后的运算中排除了所有左子树,x却不在右子树上,那么只可能是当前点的值 return key[now]; x-=less;//在右子树中还有多少值比它小,排除左子树 now=son[now][1];//继续搜索 } } }
删除操作:
void del(int v)
{ find(v); if(cnt[root]>1){//第一种情况 cnt[root]--; update(root); return; } if(son[root][0]==0&&son[root][1]==0){//第二种情况 clear(root); root=0;//将树清空 return; } if(son[root][0]==0){//第三种情况 int old=root; root=son[root][1]; fa[root]=0;//新根的父节点更新 clear(old); return; } if(son[root][1]==0){//第四种情况 int old=root; root=son[root][0]; fa[root]=0; clear(old); return; } int newroot=query_per(root),oldroot=root; splay(newroot);//将新根转上来 fa[son[oldroot][1]]=newroot; son[root][1]=son[oldroot][1];//继承右子树 clear(oldroot);//旧根归零 update(root);//更新新根 }
查找前驱后缀:
int query_pre(int x) { splay(x);//日常旋转 int now=son[root][0]; while(son[now][1]!=0)now=son[now][1]; return now; } int query_next(int x) { splay(x); int now=son[root][1]; while(son[now][0]!=0)now=son[now][0]; return now; }
splay完结。
图片以及部分代码来源:lazy_people。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号