浅谈拉格朗日插值公式

拉格朗日差值公式：

拉格朗日插值法

在数值分析中，拉格朗日插值法是以法国十八世纪数学家约瑟夫，拉格朗日命名的一种多项式差值方法。——百度百科

 

为什么学它？

在oi中，可以水这道题。。

 

在以后的日常生活中，我们有些人在给机器编程的过程中可能会遇到一些模型中的函数，不能用实际的代数，或者机器的数据来准确的模拟这个函数的表达（比如sinx，这个函数的准确值的求法着实让人摸不着头脑。），sinx很抽象，但是我们完全可以在sinx上多取很多点，使得用多项式能够近似表达。而多项式可以带入数据准确的求得其函数值。

如果你要用机器加工一个外形波浪（sinx）的零件，你完全可以按照拉格朗日插值法求得一个多项式来近似表达它的外形，从而加工出光滑的波浪表面。

在其他方面应用也很广泛。

开始学习：

众所周知，n个二维坐标系上的不同的点能够确定唯一一个最高次为n-1多项式。

有些题需要或者需要类似的知识。

引入拉格朗日插值公式：

拉格朗日插值公式就是根据给你的点来O（n^2）求那个多项式的系数。

根据带入的点，我们可以得到这样一种方案：

每一个点“掌管”多项式的一部分，多项式由n部分组成，当带入一个点的横坐标xi时，其他的部分中都带有（x-xi）这一个因式使得其值为0，最后xi“掌管”的那部分中没有这个因式使得这一部分的值为（xi，yi）中的yi。

根据这个原则，带入所有的点的横坐标都满足纵坐标等于其对应的值，我们找到了那个多项式。

f（xk）表示取第k个x值时它所对应的那一部分的值。

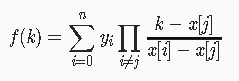（图片来源luogu）

可以感知到，当x取xi之外的值时，k-x[j]肯定有一项为0，进而约去整个部分。

 

 当然，取这些x之外的值的时候所有部分一起发挥作用，而不是约去。

关于其进阶：

拉格朗日在x取值连续的时候可以被优化成连乘的形式进行O（n）求解。这里不再深入讲述，真正深入研究者们可以浏览其他dalao博客自行学习。

例题P4781 拉格朗日插值：

裸板子题，O（n^2）求解。

代码：

#include<cstdio>
#include<cstring>
#include<iostream>
#define modd 998244353
#define ll long long
#define N 2003
ll read()
{
    ll ans=0;
    char ch=getchar(),last=' ';
    while(ch<'0'||ch>'9')last=ch,ch=getchar();
    while(ch>='0'&&ch<='9')ans=(ans<<3)+(ans<<1)+ch-'0',ch=getchar();
    return last=='-'?-ans:ans;
}
ll n,k,x[N],y[N],ans;
ll ksm(ll now,ll ur)
{
    ll anss=1;
    while(ur>0)
    {
        if(ur&1)anss=anss*now%modd;
        now=(now*now)%modd;
        ur>>=1;
    }
    return anss;
}
int main(){
    n=read(),k=read();
    for(int i=1;i<=n;i++)
        x[i]=read(),y[i]=read();
    for(int i=1;i<=n;i++)
    {
        ll up=1,down=1;
        for(int j=1;j<=n;j++)
        {
            if(i==j)continue;
            up=(up*(k-x[j]+modd)%modd)%modd;
            down=(down*(x[i]-x[j]+modd)%modd)%modd;
        }
        ans=(ans+y[i]*up%modd*ksm(down,modd-2)%modd)%modd;//除法取模不能直接模，求逆元 
    }
    printf("%lld",ans);
    return 0;
}

完结。希望对各位的学习有所帮助。