洛谷P3374 【模板】树状数组 1&&P3368 【模板】树状数组 2题解
图片来自度娘~~
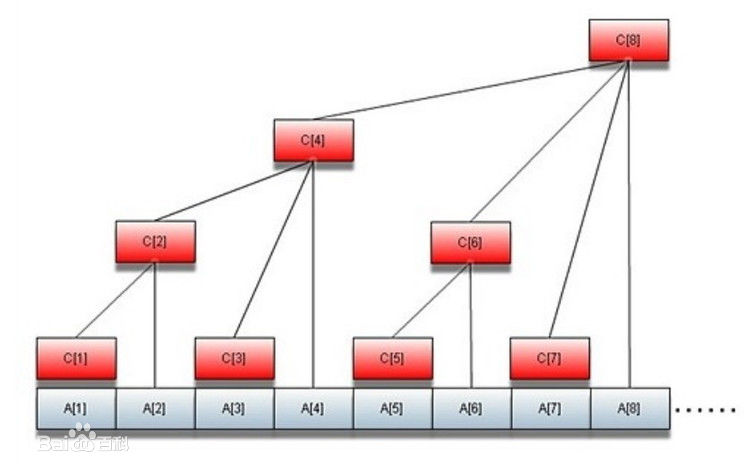
树状数组形如上图,是一种快速查找区间和,快速修改的一种数据结构,一个查询和修改复杂度都为log(n),树状数组1和树状数组2都是板子题,在这里进行详解;
求和:
首先我们看一看这个图’
A数组对应各个元素的值,c数组用来求和和修改。
有连线代表着此节点的值为连线下全部子节点的和such as c[4]=c[2]+c[3]+A[4]=A[1]+A[2]+A[3]+A[4];
貌似没有什么神仙规律。。。。。。小学找规律题都不会了嘤嘤嘤
那么我们看一下:
C1 = A1 对应的:1=2^0
C2 = A1 + A2 2=2^1
C3 = A3 3=2^1+2^0
C4 = A1 + A2 + A3 + A4 4=2^2
C5 = A5 5=2^2+2^0
C6 = A5 + A6 6=2^2+2^1
C7 = A7 7=2^2+2^1+2^0
C8 = A1 + A2 + A3 + A4 + A5 + A6 + A7 + A8 8=2^3
那么我们按照右边的拆分,如果要询问前7个元素(前7个A的和)的和,那么我们可以把7分成如上的3个分段(区间),分别预处理这3个区间的和,把时间复杂度降到log级别的而不是分别查找7个元素并累加7次。
那么我们找到了降低时间复杂度的方法了,但是怎么实现?
换句话说怎么把一个数拆成这种区间呢?
这里我们用一个神奇的东西叫做lowbit(x), 用来一位一位的把x拆分成以上这种形式。
我们发现,以上的形式就是一个数的二进制分解!
那么我们在将一个任意自然数表示成二进制的时候,只要每次获取这个数二进制表示的最后为值为1的一位,并每次减去它,直到这个数为0为止才算拆分完。
看着很懵?QWQ
我们还是要拿7举个栗子:
7=2^2+2^1+2^0,也就是7用二进制表示为111;
那么我们获取当前数二进制表示的最后为值为1的一位以及它后面所有的0构成的数,也就是最后的1,表示长度为1的区间,获取完毕后,我们减去c[7];现在数变为110,和ans加上c[7]
我们获取当前数二进制表示的最后为值为1的一位以及它后面所有的0构成的数,也就是第二位的1,表示长度为2的区间,获取完毕后,我们减去c[7-1]也就是c[6];现在数变为100,和ans加上c[6]
我们获取当前数二进制表示的最后为值为1的一位以及它后面所有的0构成的数,也就是开头的1,表示长度为4的区间,获取完毕后,我们减去c[6-2]也就是c[4];现在数为0,和ans加上c[4]
那么,我们成功把前7个数的和分解为c[7],c[7-2^0]和c[7-2^0-2^1]三个区间,对照上图,我们发现ans成功表示了前7个数(A)的和。你看一下就知道了嘛。。。QWQ
lowbit(x)公式就是x&(-x),
这是啥
1.我们对原数先取反,(就是在二进制表示下0变1,1变0,7(111)取反为000)
2.然后加一(000+1=001)
3.然后进行&运算(对于当前二进制数位,如果都相同(同为1或0),就返回1,else就为0)(111&001=1)
那么lowbit(7)就位1,即从右往左数数到第一个非零位的数和它后面所有的0构成的数。
概念算是讲清了,那么公式也讲一下:
对于第一步:x=~x
第二步:~x+1也就是-x,具体为什么要看电脑存储原理二进制补码,来源度娘。
第三步,与运算:x&(~x+1)也就是x&-x
至此,求和方法讲解完毕;
求和函数代码:
int query(int x){ int ans=0; while(x!=0){ ans+=tree[x]; x-=lowbit(x); } return ans; }
修改:
对于修改操作,只要查把后面元素和当前项有关的都加上修改的值就OK了,换句话说就是只要当前项能够影响到的后面的项,就都修改。
也就是把-lowbit(x)换成+lowbit(x)其余没大区别
代码:
void update(int x,int k){ while(x<=n){//上界 tree[x]+=k; x+=lowbit(x); } }
然后,树状数组1差不多讲完了。。
树状数组1总代码:
#include<iostream> #include<cstdio> #include<algorithm> using namespace std; const int maxn=500500; int n,m; int tree[maxn<<2]; int lowbit(int k){ return k&(-k); } void update(int x,int k){ while(x<=n){ tree[x]+=k; x+=lowbit(x); } } int query(int x){ int ans=0; while(x!=0){ ans+=tree[x]; x-=lowbit(x); } return ans; } int main(){ scanf("%d%d",&n,&m); for(int i=1;i<=n;i++){ int a; scanf("%d",&a); update(i,a); } for(int i=1;i<=m;i++){ int a,b,c; scanf("%d%d%d",&a,&b,&c); if(a==1)update(b,c); else printf("%d\n",query(c)-query(b-1)); } }
接下来是树状数组2
有些不同。
因为树状数组2变成了区间修改,单点询问,而区间修改如果用原来的方法会导致严重TLE。
那么这里我们就要用差分的方法来做这道题。
cha[i]表示a[i]-a[i-1]的值,特别的,cha[1]=a[1],因为我们设a[0]=0,那么我们,每一个数的值就可以用这个数的前缀和来表示。而这符合树状数组的求和方式。
对于区间修改,你只要修改两个值:
update(a,k);update(b+1,-k);
也就是把差分数组两边的值修改一下,区间的值就可以整体变化了。
代码如下:
#include<iostream> #include<cstdio> using namespace std; int read() { int ans=0; char last=' ',ch=getchar(); while(ch<'0'||ch>'9') { last=ch,ch=getchar(); } while(ch>='0'&&ch<='9') { ans=(ans<<3)+(ans<<1)+ch-'0'; ch=getchar(); } return last=='-'?-ans:ans; } int n,m,c[500001],before=0,now,judge,a,b,k; int lowbit(int x) { return x&(-x); } void update(int x,int y) { for(;x<=n;x+=lowbit(x))c[x]+=y; } int sum(int x) { int ans=0; for(;x;x-=lowbit(x))ans+=c[x]; return ans; } int main(){ n=read();m=read(); for(int i=1;i<=n;i++) { now=read(); update(i,now-before);//存入差分数组而不是原数组 before=now; } for(int i=1;i<=m;i++) { judge=read(); if(judge==1) { a=read(),b=read();k=read(); update(a,k);update(b+1,-k);//不同的操作 } else { a=read(); printf("%d\n",sum(a)); } } return 0; }
完结撒花!


 浙公网安备 33010602011771号
浙公网安备 33010602011771号