图的基础和遍历

1.图的定义

图中的数据元素称为点(Vertex)，连接这些顶点的线称为边(Edge)或者弧(Arc)，前者是在无向图(Undigraph)中的名称，而后者是有向图(Digraph)中的术语，指向的点称为弧尾，而发出的点称为弧头。

完全图(Completed graph)是指所有点之间都有连边的无向图，即如果有n个点，将会有n(n-1)/2条边。

                

 

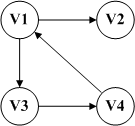
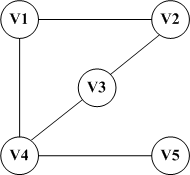
上图左边即为一个有向图，右图是一个无向图。我们可以分别表示为：

G1=(V1,{E1})       V1={v1,v2,v3,v4}     E1={<v1,v2>,<v1,v3>,<v3,v4>,<v4,v1>}

G2=(V2,{E2})       V2={v1,v2,v3,v4,v5}        E2={(v1,v2),(v1,v4),(v2,v3),(v3,v4),(v4,v5)}

如果图的边或者弧有权重的情况下，我们叫这个图为网(Network)。

2.邻接点和度

假如两个图G1=(V1,{E1})，G2=(V2,{E2})，如果V1是V2的子集，E1也是E2的子集，那么可以称G1是G2的子图(Subgraph)。

对于无向图，一条边上的两个点称为邻接点(Adjacent)，或两个点相邻接。而该边依附于这两个节点，或者说该边与这两个点相关联。顶点的度(Degree)指的是该顶点相关联的边的数目。

而对于有向图，一个弧从A点连接到B，称A邻接到B，或者B邻接自A。入度(Outdegree)指以该节点为弧尾的弧数目，同样出度(Indegree)指以该节点为弧头的弧数目。

3.路径和连通

从点A到B的路径(Path)是指一个从A到B的顶点序列，其中每两个连接的顶点都有边或者弧。路径的长度是路径上点的个数。

如果第一个顶点和最后一个顶点相同，则称该路径为回路或者环(Cycle)。如果路径中点不重复则成为简单路径。

无向图中，如果任意两个节点都能连通，则称该图为连通图(Connected Graph)。非连通图中个连通子图称为连通分量(Connected Component)。有向图中上面两个名词为强连通图和强连通分量。

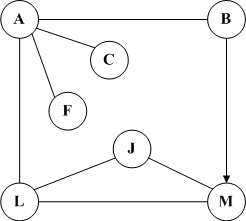
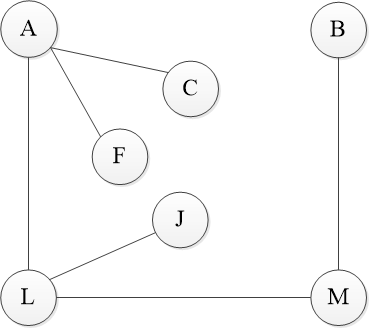
4.最小生成树

最小生成树是指包含无向连通图中所有的节点，但是仅需要n-1条边将它们相连。在译可生成树上添加任意一条边，必定会构成一个环。如下图所示右图是左图的最小生成树。