AVL树的介绍和实现
一、AVL树
AVL树是一种自平衡二叉查找树，因此在了解AVL树之前先介绍一下平衡二叉树。所谓平衡二叉树即该树中的任一个节点的左子树和右子树高度差不会超过1。如下图左是平衡二叉树，而右图则不是。节点40的左子树高度为1，而右子树高度为3，这样就相差了2，所以不是一个平衡二叉树，平衡树其实并不注重节点的顺序，所以应用更多的一般是平衡二叉查找树。相比于普通的二叉查找树，AVL能够避免由于插入顺序导致子树高度不平衡，甚至退化为链表的情况，能够最大化期望查找效率，使得查找时间复杂度为O(logn)。
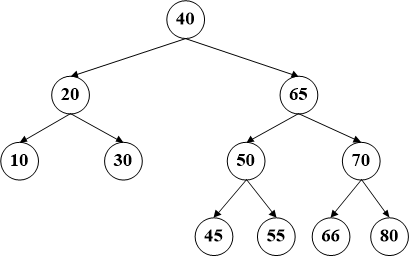
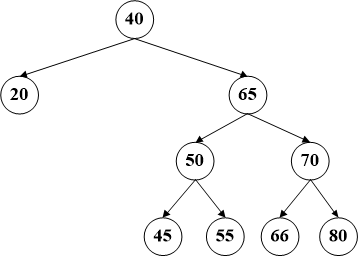
二、如何实现平衡
在一个新的节点插入后，不平衡的情况均为以下四种情况之一，分别称其为LL，RR，LR和RL。下面四个图分别代表这四种情况。
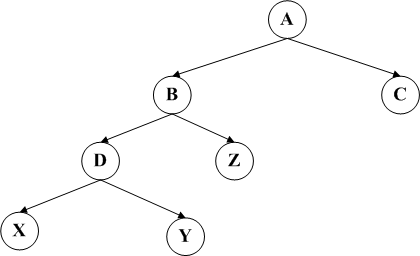
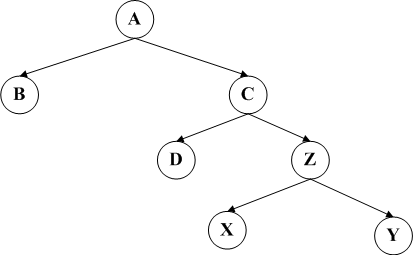
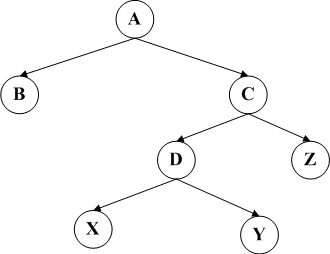
LL和RR旋转的方案分别是
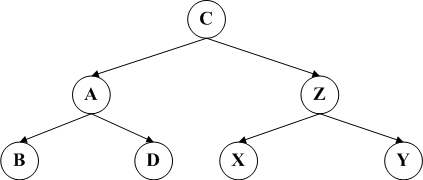
而LR和RL要稍微复杂一些，需要经过两次旋转，前者需要先RR后LL的旋转方案，而后者需要先LL后RR的旋转方案。
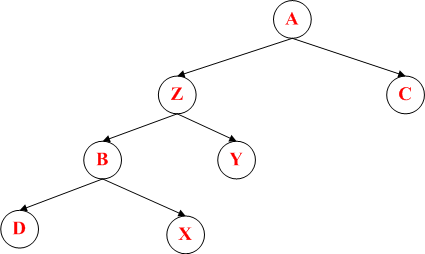
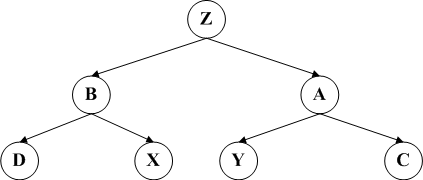
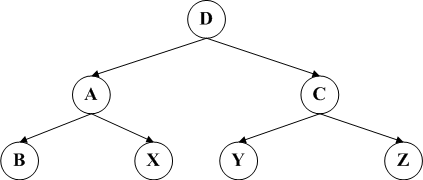
上述红色节点代表是经过一次旋转后的结果，而黑色图代表最终结果。两个分别代表LR和RL的旋转方案。
三、最终的实现
