(二) 关系数据模型
1.关系数据库和关系模式
在关系数据库中,我们用关系来表示实体集和联系集,关系通常使用二维表来表示,对应关系名。表的每一列称为属性(和ER图中的可以认为是一样的);每一行可以称为一条记录;这里每个属性都需要是原子的,这决定了规范的关系数据库中不能有多值属性和复合属性。
什么是关系模式?其实关系模式可以简记为:
R(A1,A2,…,An) 其中R为关系模式名,A表示属性名。
一个关系(我的理解就是一个实际的数据库表)就就可以称为该关系模式的一个关系值。【型和值的对应,理解】
除了关系的超码、候选码和主码值外,还有一些定义,比如任意候选码中的属性就可以称为是主属性,而不在任何码中的属性即为非主属性。外码(外键),即不为本关系的主键,但是是其他关系的主键,就称为该关系的外键。
例如:
学生表(学号,姓名,性别,班级)
其中每个学生的学号是唯一的,学号就是一个主键
课程表(课程编号,课程名,学分)
其中课程编号是唯一的,课程编号就是一个主键
成绩表(学号,课程号,成绩)
成绩表中单一一个属性无法唯一标识一条记录,学号和课程号的组合才可以唯一标识一条记录,所以 学号和课程号的属性组是一个主键
成绩表中的学号不是成绩表的主键,但它和学生表中的学号相对应,并且学生表中的学号是学生表的主键,则称成绩表中的学号是学生表的外键
同理 成绩表中的课程号是课程表的外键。
2.从ER图到关系模型
实体和联系都可以转换为关系,然而有时属性需要进行特殊处理,由于关系模型要求属性的原子性,所以不能出现多值属性和复合属性。至于派生属性,由于不需要进行存储,处理时直接忽略即可。对复合属性采用展平技术,即把每个子属性都当成关系模式的属性。对于多值属性,需要为其创建一个关系RM,该关系的组成遵守如下规则
- 如果多值属性M是实体E的属性,而K是E的主键,那么关系Rm的属性由M和K组成
- 如果多值属性M是联系R的的属性,并且R会涉及E1,E1,En等实体集,且主码分别是K1,K2,…,Kn,则Rm的属性由M和K1,K2,…,Kn组成
- 关系Rm的主码需要根据实际情况确定
至于实体和联系的具体处理,也会在此详细说明,每个实体集直接转为关系,实体集的属性构成关系的属性,实体集的码构成关系的码,这个可以说是相当简单了;
每个联系集也用一个关系表示,参与联系实体集的主码和联系集的属性将构成该关系的属性,而关系的码需要视联系类型而定:
- 如果是一对一联系,那么联系集转换的关系的主码可以是任一参与实体集的码(任一)
- 如果是一对多联系,那么关系的主码则是由“多”的那一端组成关系的模式(多端)
- 如果多对多联系,那么关系的主码则是由参与联系的所有实体集的主码组成的码(所有)
下面通过一个示例来进行更好的理解:
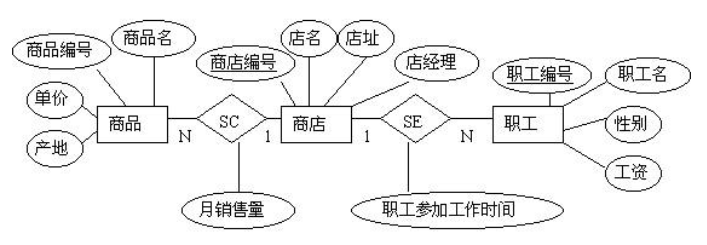
显然,实体集有商品、商店和职工,直接转为关系模式即可:
商店(商店标号,点名,店地址,店经理);商品(商品编号,商品名,单价,产地);职工(职工编号,职工名,性别,工资);
联系集有SC和SE,均为1对多的(选题失败😂),将多端的码设为主码即可,但不要忘记一端的码也会作为属性出现! 我竟然迟疑了?!
SC(商品编号,商店编号,月销售量);SE(职工编号,商店编号,参加工作时间);
3.关系的完整性约束
当然,一个关系模式不是随意转换就能变成关系的,也是有底线的。关系模型的完整性约束主要包含以下三类,分别是实体完整性、参照完整性以及用户定义完整性。
实体完整性即任意记录的主码不能出现重复的状况,也不能为空。
参照完整性即对外键的约束,即一个关系R的外键FK取值必须和其参照关系S的主码K相等,或者为空。(通俗来说就是FK的值必须和某个K相等,或者取空,不能凭空出现)
而用户定义完整性即数据必须复合满足的语义条件,例如性别只能是男或者女,年龄不能为负等。
4.关系代数
这一部分其实是为了给SQL语句打下基础,然而在真实应用场景下几乎没有(反正我是还没见过),因此不会进行过于详细的复习。
基础运算包括
(1) 选择. σF(R)表示,其中F表示逻辑判别式,R则是一个关系。选择会将F为真的行数作为结果。
有关系R如下:
| A | B | C |
| a | b | c |
| d | a | f |
| c | b | d |
| a | d | c |
执行选择操作: σB='b'(R) 的结果会将B这一列为b的行数选择出来
| A | B | C |
| a | b | c |
| c | b | d |
(2) 投影. πA1,A2,…,Ak(R)代表将这些相应的列选择出来
仍是(1)中的R,执行投影操作πA,C(R)会将A列和C列选择出来,并自动合并相同的行数:
| A | C |
| a | c |
| d | f |
| c | d |
(3) 并运算. 这是两个关系之间的运算,R∪S表示两个相同属性的关系合并到一起,但是删除相同重复的记录。
(4) 差运算. R和S的差记作R-S,S与R的差记作S-R,前者代表属于R但不属于S的集合
(5) 笛卡儿积. 记作R×S,此时R和S不必是两个属性相同的关系,即将所有可能的组合均展示出来。若R有N1行,S有N2行,那么R×S有N1*N2行。
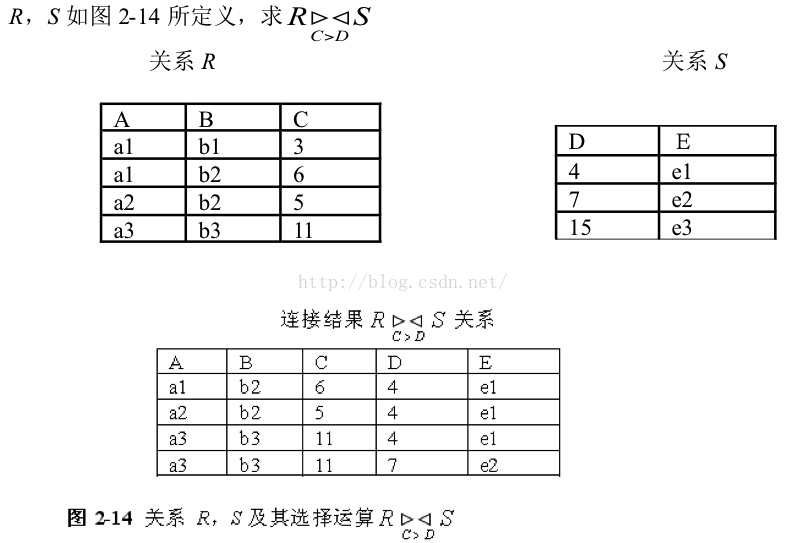
(6) 除了基础运算还有连接运算比较重要,连接运算记为R▷◁R.AθS.BS(打不出来,就是两个三角在一起),根据定义可知:R▷◁R.AθS.BS=σR.AθS.B(R×S) ,当θ表示等号时,此时称为等值连接。下面给出一个θ连接的例子
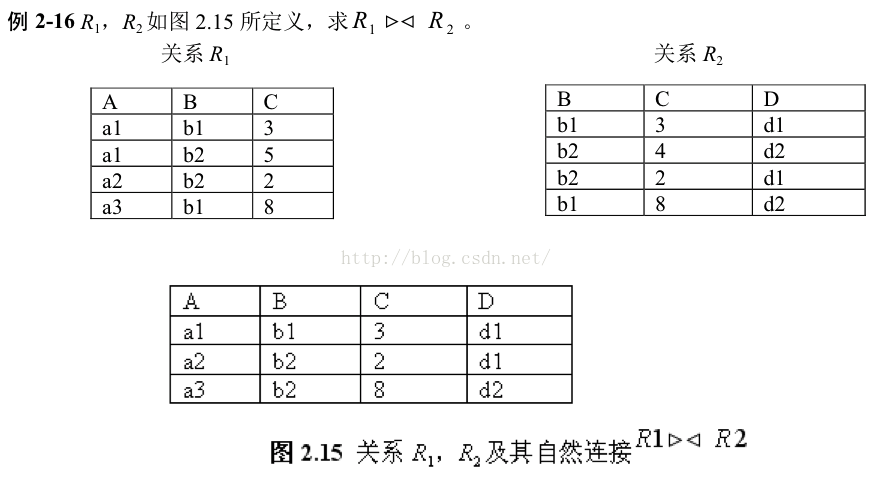
(7) 自然连接. 关系R和S的自然连接可以记为R▷◁S,代表R和S所有共同属性上的等值连接,然后去掉重复的属性。当R和S不包含相同属性时,自然连接就退化成笛卡儿积,尽管自然连接和等值连接都是根据属性值的相同进行连接,但仍有明显区别。自然连接将两个关系相同名称的属性视为一个,并且会在运算过程中进行合并。等值连接并不会这样做,不仅能够通过不同名称的属性进行连接,而且即时使用两个相同名称的属性进行连接也等同于两个不同的属性(比如会将R.A和S.A视为两个不同的属性,而自然连接就会视为同一个并且进行合并),更谈不上删除相同的属性。
除此之外,还有除法、左外连接、右外连接、全外连接等操作,这些就不一一进行介绍了。

 浙公网安备 33010602011771号
浙公网安备 33010602011771号