图

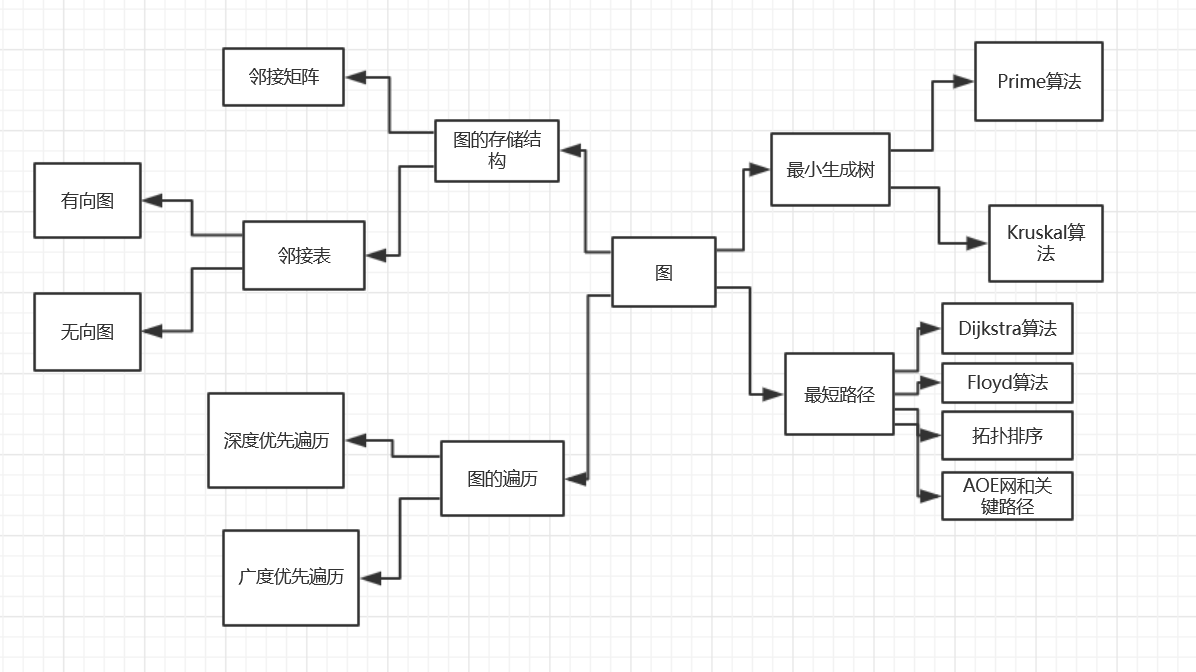
1.2 图结构学习体会

       图的深度优先遍历类似于树的先序遍历采用的搜索方法的特点是尽可能先对纵深方向进行搜索；广度优先遍历尽可能先从指定的出发点，横向的访问图中的各个顶点；

floyd算法是最简单的最短路径算法，可以计算图中任意两点间的最短路径  folyd算法的时间复杂度是O(N3),如果是一个没有边权的图，把相连的两点  间的距离设为dist[i][j] = 1，不相连的两点设为无穷大，用 floyd算法可以判断i,j两点是否有路径相连。dijkstra算法用来计算从一个点到其他所有点的最短路径的算法，复杂度O(N2)。

      当编译程序遇到错误的时候，不要慌乱，要认真阅读程序，找出错误，当错误无法排除的时候，要查阅各种文献或者向老师和同学请教，对于我们的程序调试有很大的帮助。

2.PTA实验作业（4分）

2.1 题目1：7-4 公路村村通

2.2 设计思路（伪代码或流程图）

先用邻接矩阵的方法存储图，然后就运用Prim算法求出这个图的最小生成树，最后输出最少费用。

2.3 代码截图（注意，截图、截图、截图。代码不要粘贴博客上。不用用···语法去渲染）

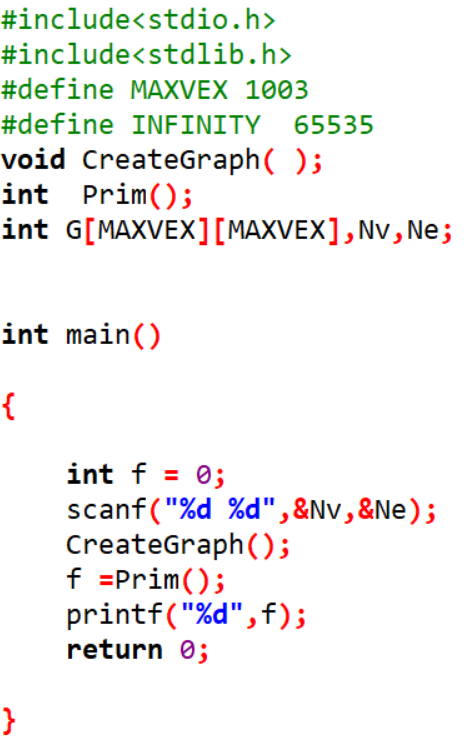
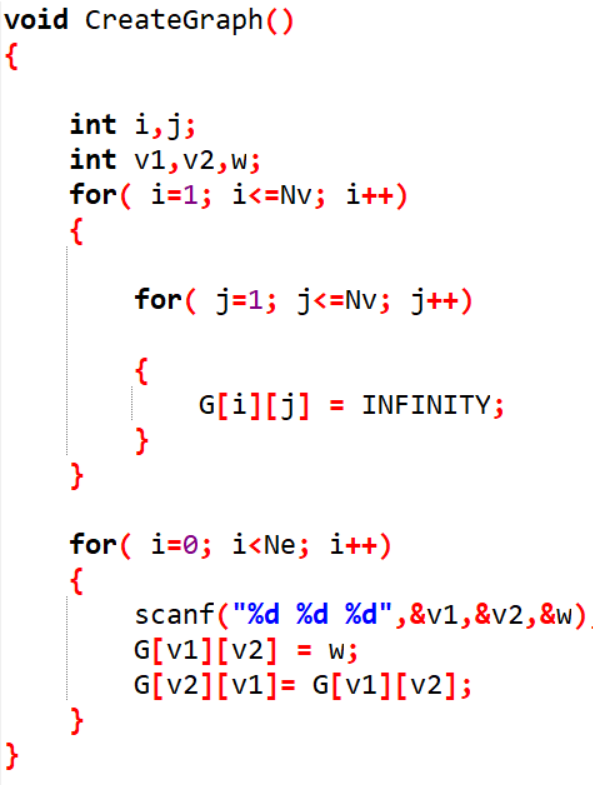
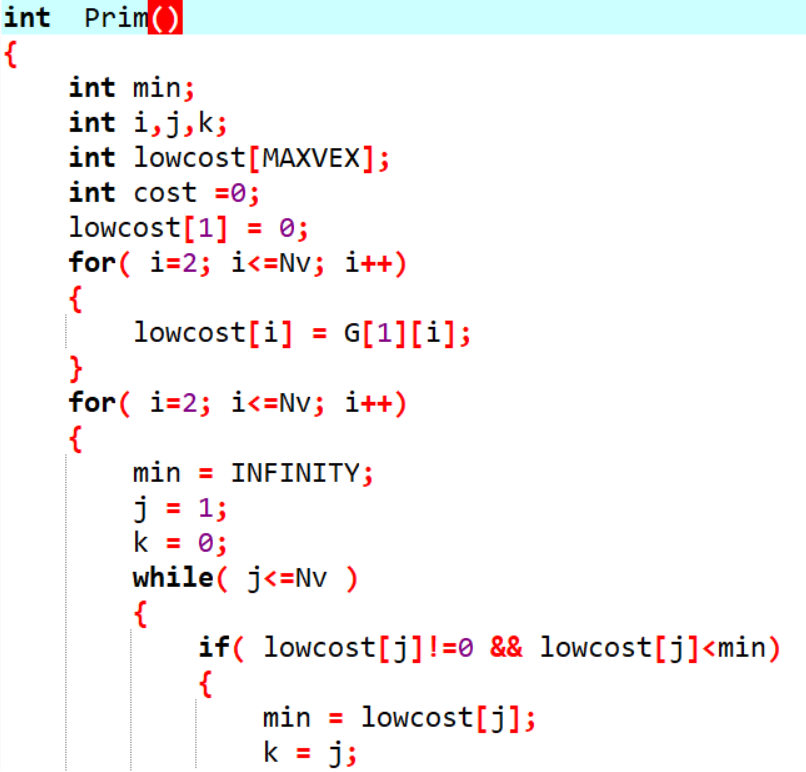
2.4 PTA提交列表说明。

 

题目2：7-5 畅通工程之最低成本建设问题

2.2 设计思路（伪代码或流程图）

 

用Prime算法求最小生成树

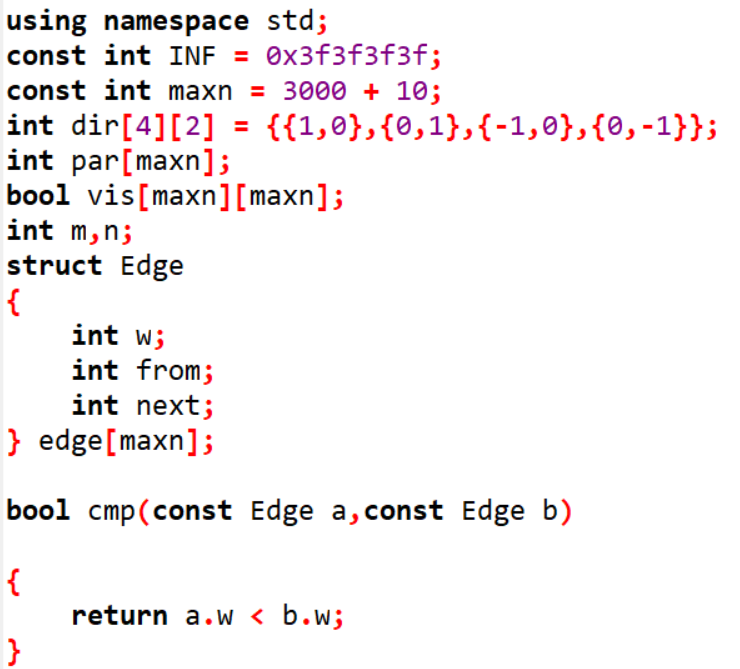
2.3 代码截图（注意，截图、截图、截图。代码不要粘贴博客上。不用用···语法去渲染）

2.4 PTA提交列表说明。

 

题目3：7-8 城市间紧急救援

2.2 设计思路（伪代码或流程图）

求最短路径长度和点权和最大值的问题,同时要记录最短路径.

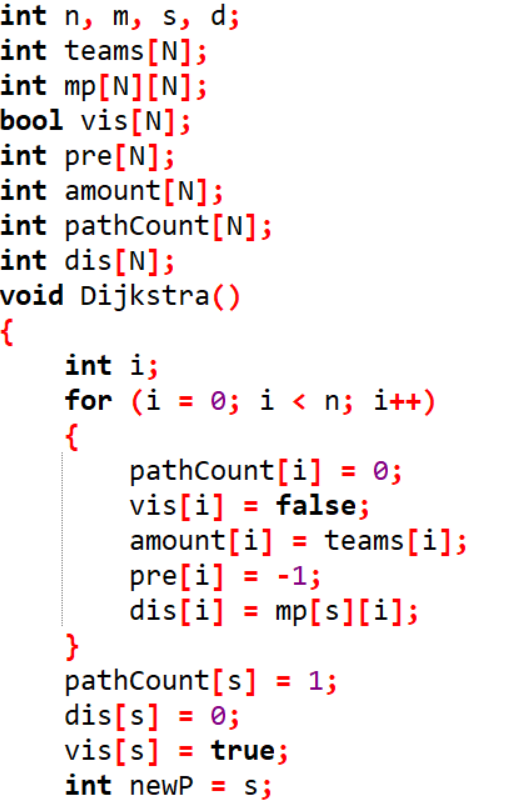
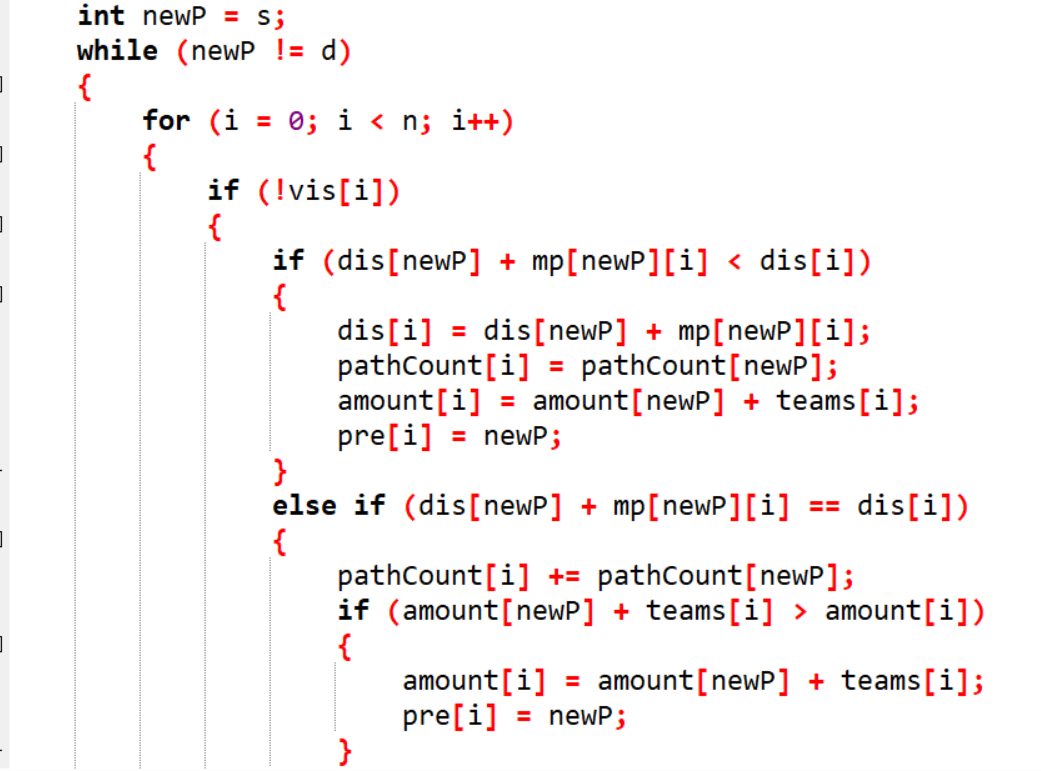
2.3 代码截图（注意，截图、截图、截图。代码不要粘贴博客上。不用用···语法去渲染）

 

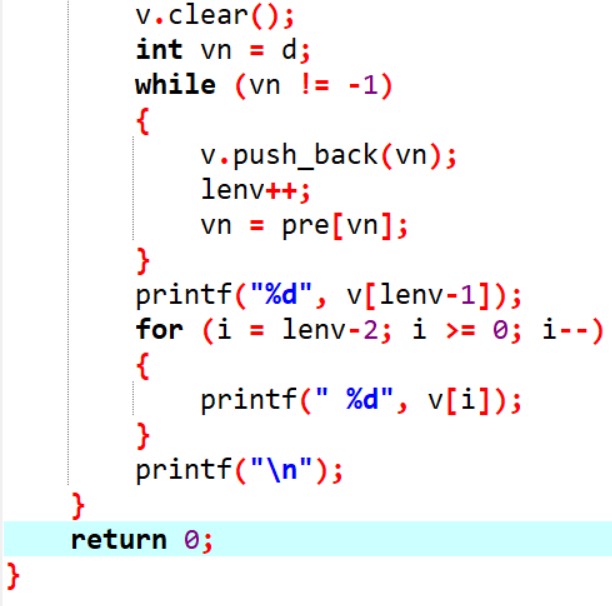
2.4 PTA提交列表说明。

 

3.截图本周题目集的PTA最后排名（3分）

 

4. 阅读代码（必做，1分）

  旅游规划：

#include <iostream>
#include <algorithm>
#include <cstdio>
#include <queue>
#include <cstring>
using namespace std;
const int inf = 0x3f3f3f3f;
int map[550][550];
int vis[550];
int val[550][550];
int dis[550];
int sum[550];
int main() {
    int n, m, s, e;
    scanf("%d %d %d %d", &n, &m, &s, &e);
    int i, j, k = 0;
    for(i = 0; i < n; i++) {
        for(j = 0; j < n; j++) {
            if(i == j) map[i][j] = 0;
            else map[i][j] = inf;
        }
    }
    int x, y, z, q;
    for(i = 0; i < m; i++) {
        scanf("%d %d %d %d", &x, &y, &z, &q);
        map[x][y] = z;
        map[y][x] = z;
        val[x][y] = q;
        val[y][x] = q;
    }
    for(i = 0; i < n; i++) {  //初始化
        vis[i] = 0;
        dis[i] = inf;
        sum[i] = 0;
    }
    dis[s] = 0;
    int minn, v;
    for(i = 0; i < n; i++) {
        minn = inf;
        v = 0;
        for(j = 0; j < n; j++) {
            if(vis[j] == 0) {
                if(minn > dis[j]) {
                    minn = dis[j];
                    v = j;
                }
            }
        }
        vis[v] = 1;
        for(j = 0; j < n; j++) {
            if(vis[j] == 0) {
                if(dis[j] > dis[v] + map[v][j]) {
                    dis[j] = dis[v] + map[v][j];
                    sum[j] = sum[v] + val[v][j];
                }
                else if(dis[j] == dis[v] + map[v][j]) {    //解题关键
                    sum[j] = min(sum[v] + val[v][j], sum[j]);
                }
            }
        }
    }
    printf("%d %d\n", dis[e], sum[e]);
    return 0;
}