《机器学习》第二次作业——第四章学习记录和心得

一、线性判据

1.两种模型

生成模型

优势

①可以根据 𝑝(𝒙) 采样新的样本数据。
②可以检测出较低概率的数据，实现离群点检测。

劣势

如果是高维的 𝒙 ，需要大量训练样本才能准确的估计 𝑝(𝒙) ；否则，会出现维度灾难问题。

判别模型

优势

快速直接、省去了耗时的高维观测似然概率估计。
最简单的判别模型：线性判据

2.线性判据

定义

如果判别模型 𝑓(𝒙) 是线性函数，则 𝑓(𝒙) 为线性判据。
可以用于两类分类，决策边界是线性的。
也可以用于多类分类，相邻两类之间的决策边界也是线性的。

优势

计算量少：在学习和分类过程中，线性判据方法都比基于学习概率分布的方法计算量少。
适用于训练样本较少的情况。

数学表达

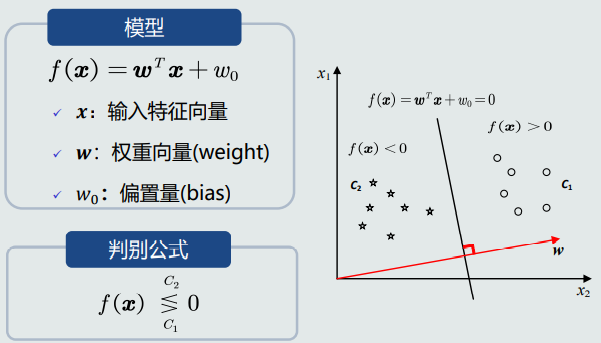
决策边界

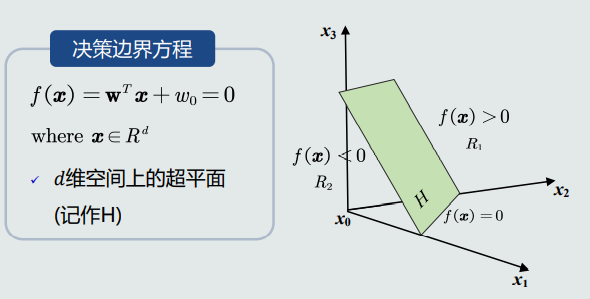
模型中 𝒘 垂直于决策边界上的任何向量，即 𝒘 垂直于决策边界H，是H的法向量。𝒘 决定了决策边界H的方向。

模型中 𝑤0 决定了决策边界的偏移量，使其能够满足两个类输出值分别为正负。

任意样本𝒙到决策边界的垂直距离为：

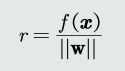
由上式可知，原点到决策边界的距离为

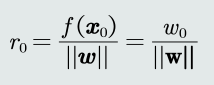
可见，𝑤0也决定决策边界相对于坐标原点的位置。

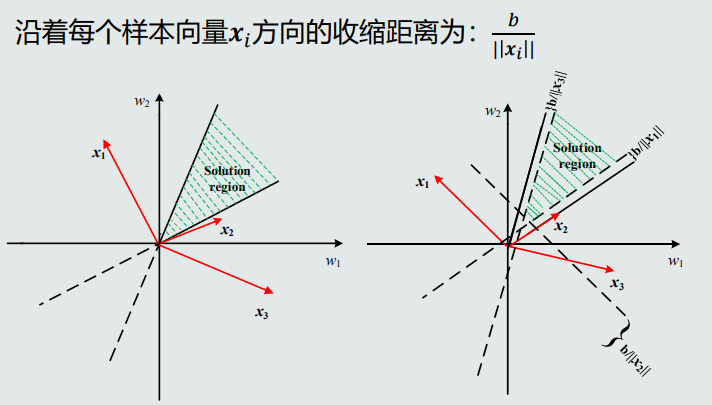
参数空间&解域

由于训练样本个数通常会远远大于参数个数（𝒘 的维度+ 𝑤0 的维度），所以线性判据满足条件的解不唯一。
学习算法就是要找到一个最优解。

参数空间

由各个参数维度构成的空间。
参数的每个可能解相当于是参数空间的一个向量。

解域

在参数空间内，参数的所有可能解所处的范围。
每个训练样本 𝒙𝑖 在参数空间定义了一个通过原点、且垂直于 𝒙𝑖 的超平面。

目标函数

常见的目标函数：误差（均方差）、交叉熵···

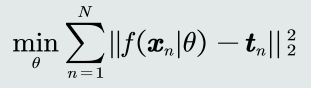
加入约束条件（例如，正则项）：提高泛化能力。

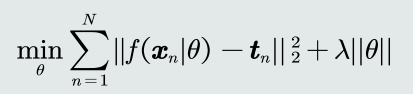
加入约束后会导致解域范围收缩。

目标函数的求解：最小化/最大化目标函数。

二、感知机算法

1.预处理

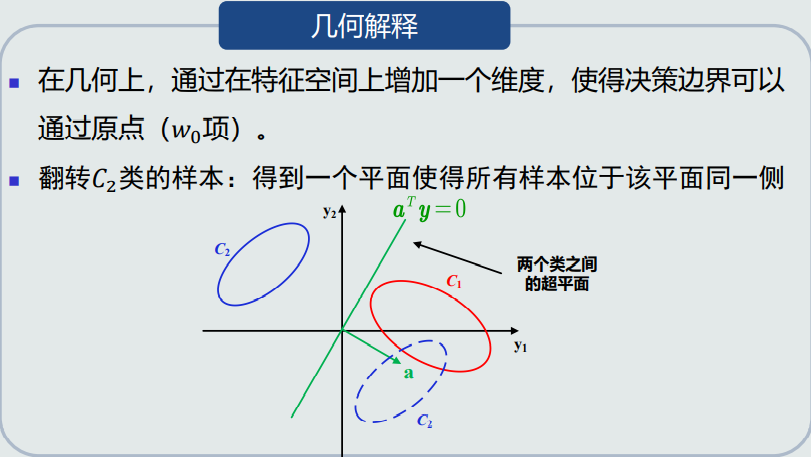
2.并行感知机

被错误分类的样本，输出值𝑓(𝒚𝑛)是负数。根据几何意义，输出值的绝对值越大，错误的程度越大。

目标函数

针对所有被错误分类的训练样本（即输出值小于0的训练样本），其输出值取反求和：

最小化该目标函数：取目标函数关于 𝒂 的偏导（即梯度）
偏导不含有 𝒂，所以不能简单的通过设置偏导为0来求解 𝒂。

梯度下降法

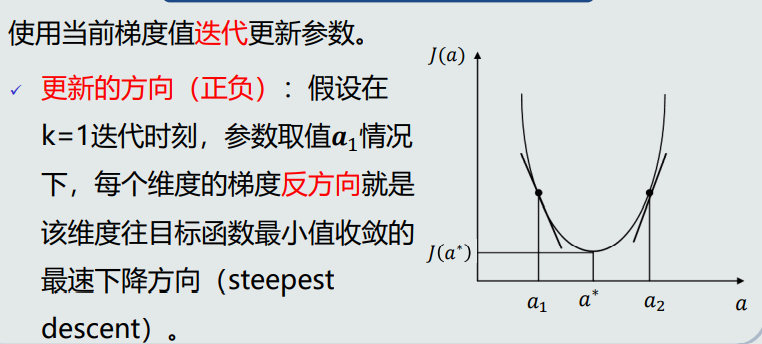
更新的大小：每个维度的梯度幅值代表参数在该维度上的更新程度。
通常加入步长(𝜂𝑘)来调整更新的幅度。每次迭代可以用不同的步长。

步长太大：可能找不到目标函数的最小值。

步长太小：迭代次数过多，不利于计算。

3.串行感知机

适用于：训练样本串行给出的情况。

目标函数

4.收敛性与最优解

如果训练样本是线性可分的，感知机（并行和串行）算法理论上收敛于一个解。

步长决定收敛的速度、以及是否收敛到局部或者全局最优点。

如果目标函数J(a)满足L-Lipschitz条件（对于任意a，存在一个常数L，使得|J(a)|<L成立），则步长𝜂 = 1/ 2𝐿 可确保收敛到局部最优点。

如果目标函数J(a)是凸函数，局部最优点就是全局最优点。

5.约束

三、Fisher线性判据

1.Fisher判据基本原理

找到一个最合适的投影轴，使两类样本在该轴上投影的重叠部分最少，从而使分类效果达到最佳。
最佳标准之一：投影后，使得不同类别样本分布的类间差异尽可能大，同时使得各自类内样本分布的离散程度尽可能小。

类间样本的差异程度

用两类样本分布的均值之差度量。

类内样本的离散程度

用每类样本分布的协方差矩阵表征。

2.目标函数

3.目标函数求解

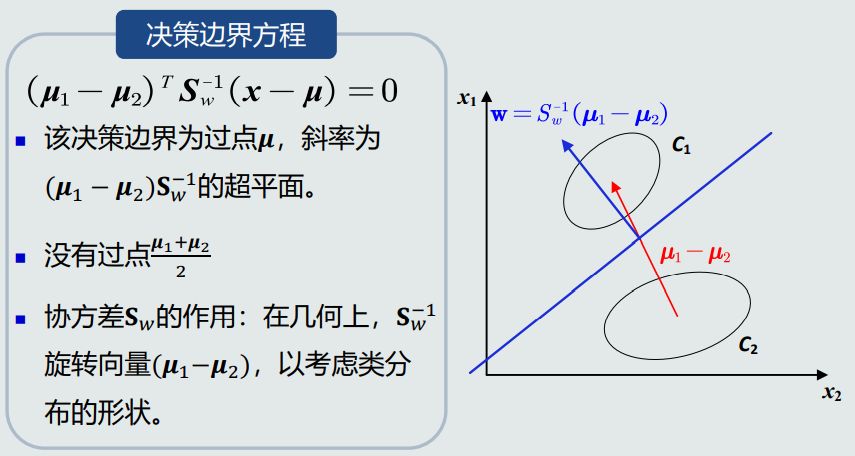
4.决策边界

四、支持向量机

1.设计思想

给定一组训练样本，使得两个类中与决策边界最近的训练样本到决策边界之间的间隔（离决策边界最近的训练样本到决策边界的垂直距离）最大。

2.支持向量

总间隔

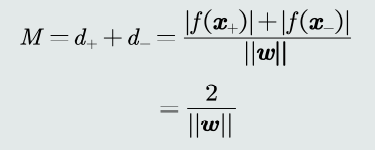
3.目标函数

支持向量机的目标：最大化总间隔。
最大化间隔，等价于最小化| 𝒘 |，所以目标函数设计为：

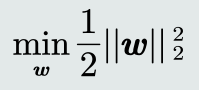
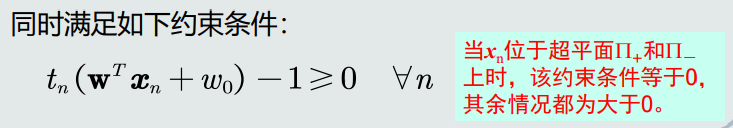
支持向量机的目标函数是一个条件优化问题。
拉格朗日乘数法是常用的解决该类问题的方法。

4.拉格朗日乘数法

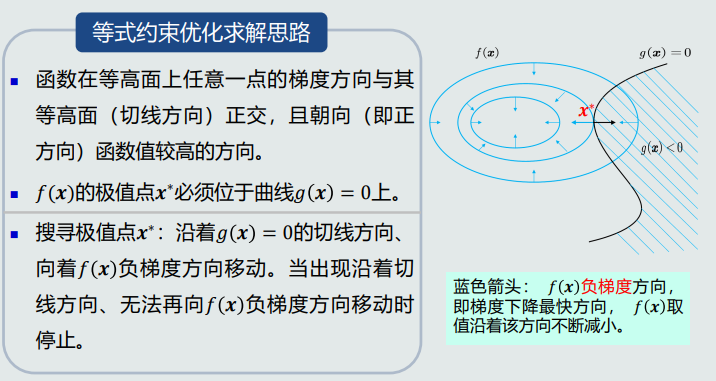
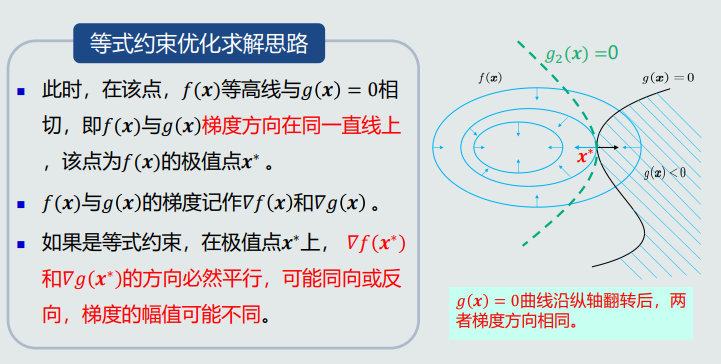
等式约束问题可以转换为等价的不带约束的优化问题

五、线性判据多类分类

多类分类的本质是非线性的，通过多个线性模型组合的途径实现多类分类。

1.One-to-all策略

假设每个类与剩余类线性可分。
对每个类单独训练一个分类器，𝐾个类需要训练𝐾个分类器，用于判别属于或不属于对应的类。
有时也可以只训练𝐾 − 1 个分类器：针对某个测试样本𝒙，如果所有𝐾 − 1个分类器都输出为非正值，则代表该样本属于剩余的第𝐾个类。
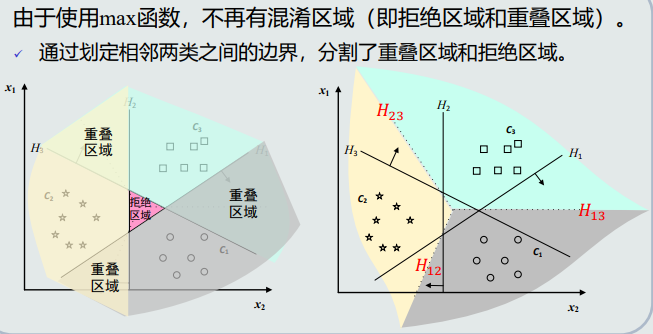
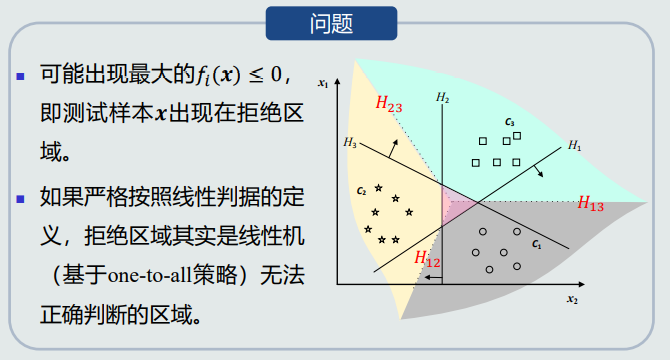
可能出现混淆区域：针对具体的某一个样本，该样本不属于任何一类（拒绝选项）或者属于多个类（重叠）的情况。

2.线性机

假设每个类与剩余类线性可分。
在One-to-all策略的分类器基础上，给定测试样本𝒙，其属于所有分类器中输出值最大的那个类。
输出值𝑓𝑖 (𝒙) 近似于𝒙 到分类边界（𝐶𝑖类与剩余类）的距离。该值最大即表示属于该类的可能性大。
输出值投票法（max函数）

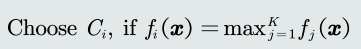
线性机的决策过程相当于：将输入特征𝒙直接映射到类别标签𝑙。

线性机 = 𝐾个线性模型 + 一个max函数

3.One-to-one策略

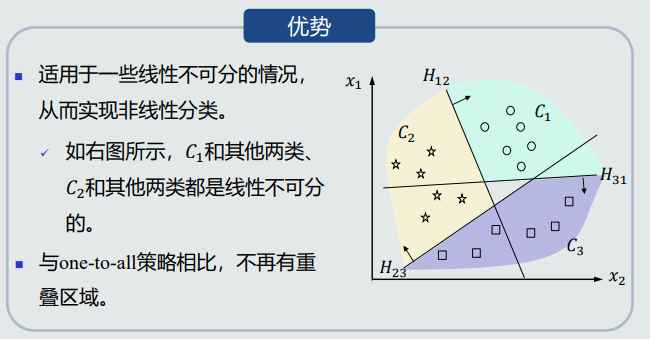
假设任意两个类之间线性可分，但每个类与剩余类可能是线性不可分的。
针对每两个类𝐶𝑖 和𝐶𝑗 ，训练一个线性分类器，总共需要训练𝐾(𝐾 − 1)/2个分类器。避免了one-to-all策略正负类样本个数不均衡的问题。
𝐶𝑖类与剩余类的决策边界：所有𝐻𝑖𝑗正半边的交集。

六、线性回归

输出的数据类型是连续的。

如果参数𝑾是最优的，意味着对每个样本(𝒙𝑛, 𝒕𝑛)而言，模型的输出值𝒚𝑛与标定的输出真值𝒕𝑛之间的差值最小。因此目标函数使用均方误差即最小化均方误差

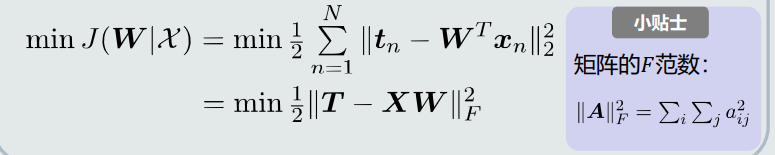
展开后

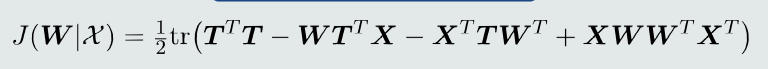
求偏导

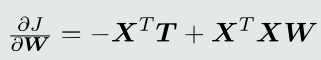
最小二乘法适用于Tall数据

七、逻辑回归

1.Logit变换定义

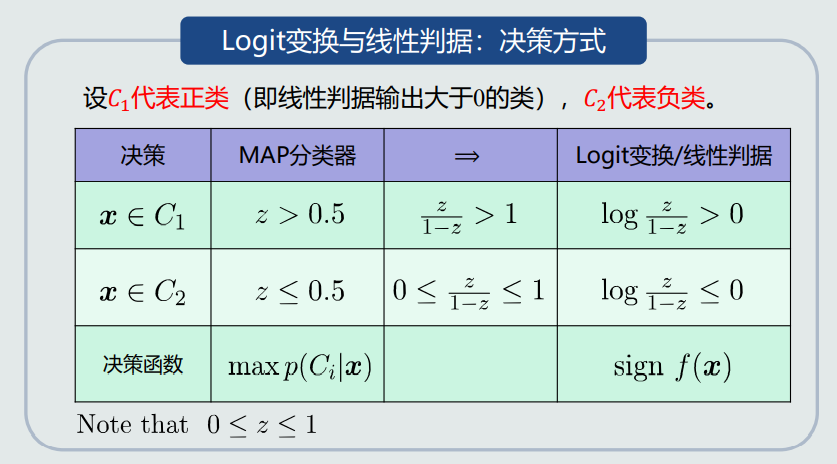
2.Sigmoid函数

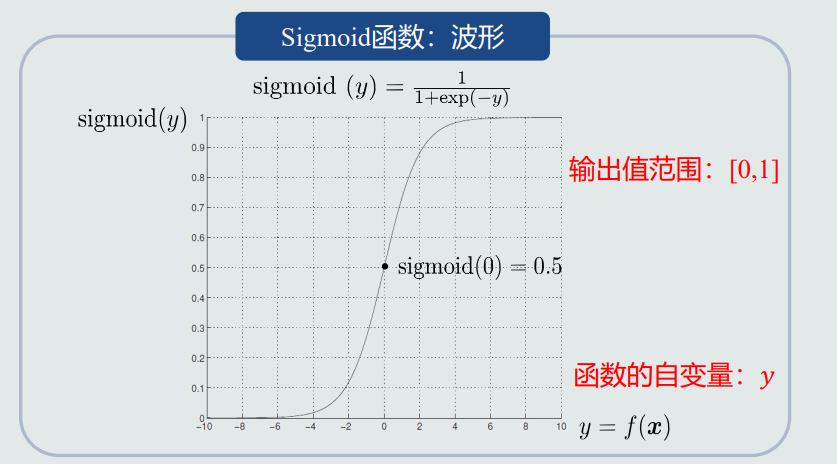
3.逻辑回归

定义

决策边界

单个逻辑回归就是一个神经元模型，激活函数是Sigmoid函数。
多个逻辑回归（即多个同层神经元）可应用于多类分类，使用max函数做决策（即基于one-to-all的线性机）。

4.几种模型对比

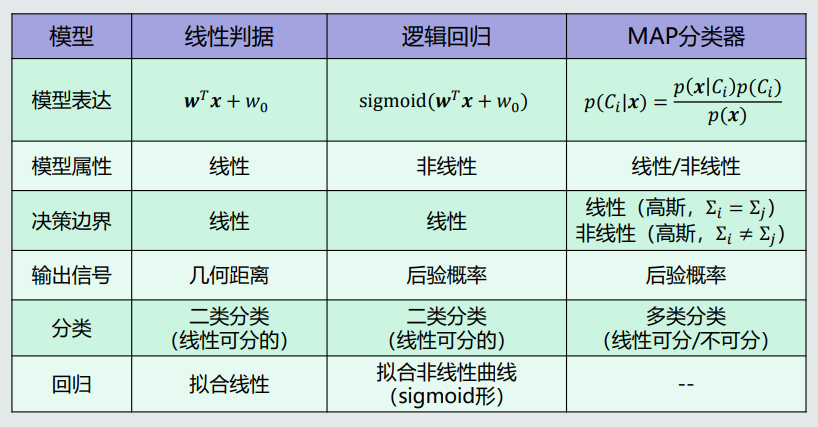
八、Softmax判据

单个模型实现多分类。

1.Softmax函数

2.Softmax判据

3.决策边界

4.对比

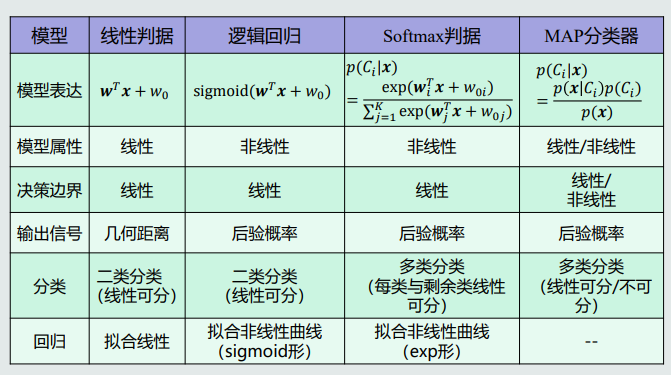
九、核支持向量机

1.基本思想

将线性不可分的样本通过一个函数𝜑映射到一个高维的特征空间（Φ空间）使得其线性可分

2.核函数

3.决策模型

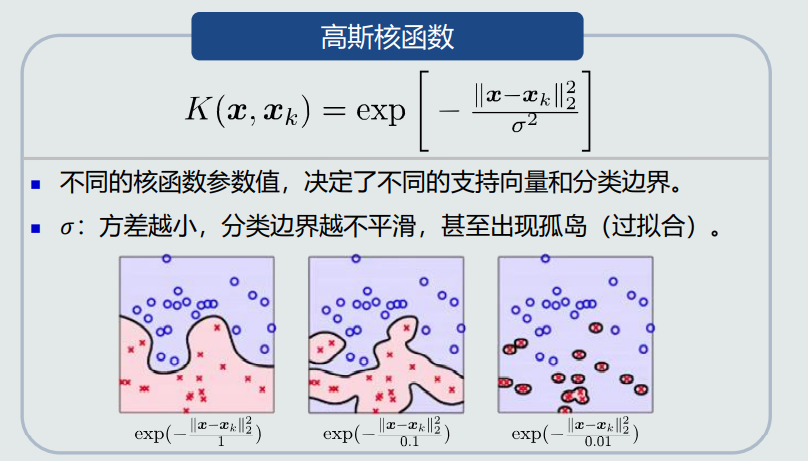
4.常见的核函数

Mercer条件：只要是半正定对称函数，都可以用作核函数。