数据结构——AVL平衡树
1、简介
前面讲过了二叉搜索树,简单复习一下二叉搜索树的定义。二叉搜索树每个节点至多有2个分支,对于任意一个节点,左子树上所有的节点值均小于它根节点的值,右子树上所有的节点值均大于它根节点的值。
那么根据定义,假如有一个有序数组[1, 2, 3, 4, 5],将其添加到二叉搜索树会怎样呢
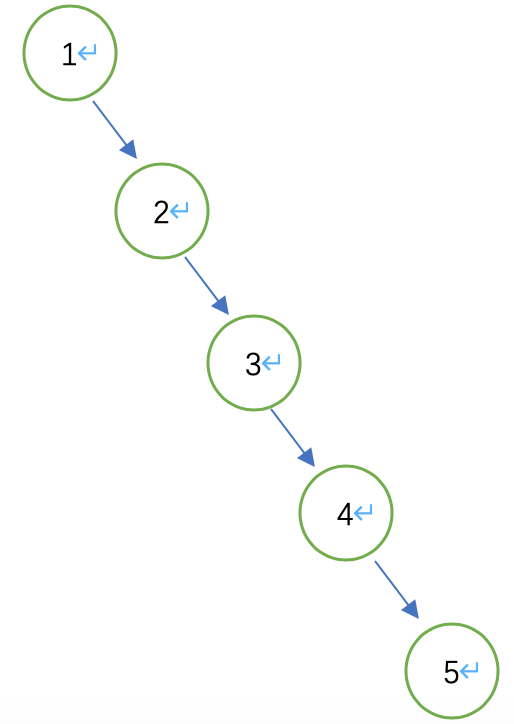
由于后插入的值都大于前面所有节点的值,所以总是会插入到右节点,此时它退化成一个单链表了
可以发现,普通二叉搜索树对于有序数据的处理并不完美,它存在左右子树高度差过大甚至退化成链表的可能性,而对于一个树结构来说树高度会直接关乎查找效率。针对这一情况,我们引入了AVL自平衡树。
对于AVL树,有如下定义:
- 本身是一颗二叉搜索树
- 每个节点的左右子树高度差最多为1
2、平衡思路
AVL树实现平衡主要是在增加和删除这两个操作中增加了一个”旋转“概念来实现的。
为了明确平衡这一概念,我们引入一个平衡因子。对于任意节点的平衡因子等于左右子树的高度差,当-1<=平衡因子<=1时,说明左右子树高度差最多为1,该节点处于平衡状态。
计算平衡因子需要获取左右子树的高度,因此对于每一个节点,我们可以在内部维护一个变量height,记录其在二叉树中的高度。
准备工作做好之后,我们来分析一下对一个已经实现平衡的二叉搜索树增加一个节点可能引发的几种不平衡情形:
- LL型
y
/ \
x T4
/ \
z T3
/
T1
这上面这个树结构中,T1是新增加节点的位置。可以看到,在增加T1之前,对于任意节点左右子树平衡因子不大于1,整个二叉树处于平衡状态。
当加入T1后,对于x节点,左子树高度2,右子树高度1,处于平衡,对于y节点,左子树高度3,右子树高度1,平衡因子为2,不满足平衡。
对于这种情形,由于新增加的节点T1位于y节点左子树的左子树,因此将其称之为LL型。
- LR型
y
/ \
x T4
/ \
z T3
\
T1
新增加的节点T1位于y节点左子树的右子树,称之为LR型。
- RR型
y
/ \
T1 x
/ \
T2 z
\
T3
新增加的节点位于y节点右子树的右子树,称之为RR型。
- RL型
y
/ \
T1 x
/ \
T2 z
/
T3
新增加的节点位于y节点右子树的左子树,称之为RL型。
上面列举了所有可能出现的不平衡情况,解决不平衡我们可以通过”左旋转“和”右旋转”来实现。
以LL型为例,y节点的平衡因子为2,左子树高于右子树,我们可以想办法减少左子树高度或增加右子树高度来实现平衡。这里我们对y节点右旋转来处理:
y x
/ \ / \
x T4 向右旋转 (y) z y
/ \ - - - - - - - -> / / \
z T3 T1 T3 T4
/
T1
将y节点放置到x节点的右节点,x的原右节点T3放置到y节点的左节点,达成平衡。
RR型同理,可以对y节点左旋转:
y x
/ \ / \
T1 x 向左旋转 (y) y z
/ \ - - - - - - - -> / \ \
T2 z T1 T2 T3
\
T3
将y节点放置到x节点的左节点,x的原左节点T3放置到y节点的右节点,达成平衡。
对于LR和RL型情况就会变得复杂一点,因为如果进行一次左旋或者右旋依旧无法取得平衡,如对LR右旋
y x
/ \ / \
x T4 向右旋转 (y) z y
/ \ - - - - - - - -> / \
z T3 T3 T4
\ \
T1 T1
针对LR或RL,我们可以进行两次旋转来实现平衡,继续以LR为例,先对y的左子树x进行一次左旋转
y y
/ \ / \
x T4 向左旋转 (x) T3 y
/ \ - - - - - - - -> / \
z T3 x T1
\ /
T1 z
对x经过一次左旋转后,新的二叉树树显然是一个LL型,那么在对y进行一次右旋转就可以得到一个平衡二叉树
RL型同理,对x先右旋再对y左旋,这里就不过多赘述
3、代码实现
经过前面的实现分析,逻辑就变得比较简单了,由于AVL树只需要在二叉搜索树加入平衡判断和左右旋转,所以我们先将平衡相关的逻辑转化为代码:
class Node:
def __init__(self, key):
self.key = key
self.left = self.right = None
self.height = 1
节点增加属性height,描述节点高度
class AVLtree:
def _get_height(self, node):
# 返回node节点的高度
return node.height if node else 0
def _get_balance_factor(self, node):
# 返回node节点的平衡因子
# node节点的平衡因子,即node节点左右子节点的高度差,设定为左子节点- 右子节点
return self._get_height(node.left) - self._get_height(node.right)
def is_balance(self):
return abs(self._get_balance_factor(self.root)) <= 1
计算平衡因子的相关实现
class AVLtree:
def _right_rotate(self, y):
# 对节点y进行向右旋转操作,返回旋转后新的根节点x,旋转后会改变x、y的高度
x = y.left
temp = x.right
x.right = y
y.left = temp
y.height = 1 + max(self._get_height(y.left), self._get_height(y.right))
x.height = 1 + max(self._get_height(x.left), self._get_height(x.right))
return x
def _left_rotate(self, y):
# 对节点y进行向左旋转操作,返回旋转后新的根节点x 旋转过程中会改变x、y的高度
x = y.right
temp = x.left
x.left = y
y.right = temp
y.height = 1 + max(self._get_height(y.left), self._get_height(y.right))
x.height = 1 + max(self._get_height(x.left), self._get_height(x.right))
return x
左右旋转的代码实现
到这里我们的建立平衡所需的方法都写好了,接下来就是在增加和删除方法中增加平衡方法调用,对于增加和删除方法还是和二叉搜索树一致,这里我对增删逻辑就不多讲解,有困惑的朋友可以移步看看上篇文章数据结构——二叉搜索树。
def add(self, key):
self.root = self._add(self.root, key)
def _add(self, node, key):
# 向指定节点插入一个新节点
if node is None:
self.count += 1
return Node(key)
if key == node.key:
# 添加重复元素 什么也不干 直接返回原节点
return node
if key < node.key:
node.left = self._add(node.left, key)
else:
node.right = self._add(node.right, key)
# 更新node的height
node.height = 1 + max(self._get_height(node.left), self._get_height(node.right))
# 判断是否平衡
balance = self._get_balance_factor(node)
# 不平衡条件 balance > 1 或者 balance < -1 代表做右子节点高度差大于1
# LL
if balance > 1 and self._get_balance_factor(node.left) >= 0:
return self._right_rotate(node)
# RR
if balance < -1 and self._get_balance_factor(node.right) <= 0:
return self._left_rotate(node)
# LR 对左节点进行左旋转然后再右旋转
if balance > 1 and self._get_balance_factor(node.left) < 0:
node.left = self._left_rotate(node.left)
return self._right_rotate(node)
# RL 对右节点进行右旋钻然后再左旋转
if balance < -1 and self._get_balance_factor(node.right) > 0:
node.right = self._right_rotate(node.right)
return self._left_rotate(node)
return node
def remove(self, key):
self.root = self._remove(self.root, key)
def _remove(self, node, key):
# 删除掉以node为根的二分搜索树中值为e的节点, 递归算法
# 返回删除节点后新的二分搜索树的根
if not node:
return None
if node.key > key:
# 在左子树查找
node.left = self._remove(node.left, key)
retnode = node
elif node.key < key:
node.right = self._remove(node.right, key)
retnode = node
else:
# 找到了要删除的节点node 现在找后继节点
# 后继节点可以是左子树的最大节点,也可以是右子树最小节点
# 先考虑只有一边节点的情况
if node.left == None:
self.count -= 1
retnode = node.right
node.right = None
elif node.right == None:
self.count -= 1
retnode = node.left
node.left = None
else:
retnode = self.mininode(node.right)
retnode.right = self._remove(node.right, retnode.key)
retnode.left = node.left
node.right = node.left = None
if not retnode:
return None
# 更新node的height
retnode.height = 1 + max(self._get_height(retnode.left), self._get_height(retnode.right))
# 判断是否平衡
balance = self._get_balance_factor(retnode)
# 不平衡条件 balance > 1 或者 balance < -1 代表做右子节点高度差大于1
if balance > 1 and self._get_balance_factor(retnode.left) >= 0:
return self._right_rotate(retnode)
if balance < -1 and self._get_balance_factor(retnode.right) <= 0:
return self._left_rotate(retnode)
if balance > 1 and self._get_balance_factor(retnode.left) < 0:
retnode.left = self._left_rotate(retnode.left)
return self._right_rotate(retnode)
if balance < -1 and self._get_balance_factor(retnode.right) > 0:
retnode.right = self._right_rotate(retnode.right)
return self._left_rotate(retnode)
return retnode
至此,AVL树就构建完成了
4、效率分析
增删操作,AVL弱于BST,这是因为AVL除了实现BST的代码外,还要执行平衡判断和节点旋转来维持平衡,但总体复杂度都是O(logn)级别
查询操作,AVL快于BST,因为AVL是一颗平衡二叉树,意味着同样多的节点,AVL树的高度总不大于BST树的高度,树的高度越小,查询速度越快。
5、完整代码
class Node:
def __init__(self, key, val=None):
# 引入val,以支持map映射
self.key = key
self.val = val
self.left = self.right = None
self.height = 1
def __repr__(self):
return '<Node key=%s value=%s height=%s>' % (self.key, self.val, self.height)
class AVLtree:
def __init__(self):
self.root = None
self.count = 0
def __len__(self):
return self.count
def add(self, key, val=None):
self.root = self._add(self.root, key, val)
def get(self, node, key):
if not node:
raise KeyError('不存在的键')
if node.key == key:
return node
if node.key > key:
return self.get(node.left, key)
else:
return self.get(node.right, key)
def __getitem__(self, item):
return self.get(self.root, item)
# 向指定节点插入一个新节点
def _add(self, node, key, val):
if node is None:
self.count += 1
return Node(key, val)
if key == node.key:
# 添加重复元素 什么也不干 直接返回原节点
return node
if key < node.key:
node.left = self._add(node.left, key, val)
else:
node.right = self._add(node.right, key, val)
# 更新node的height
node.height = 1 + max(self._get_height(node.left), self._get_height(node.right))
# 判断是否平衡
balance = self._get_balance_factor(node)
# 不平衡条件 balance > 1 或者 balance < -1 代表做右子节点高度差大于1
# LL
if balance > 1 and self._get_balance_factor(node.left) >= 0:
return self._right_rotate(node)
# RR
if balance < -1 and self._get_balance_factor(node.right) <= 0:
return self._left_rotate(node)
# LR 对左节点进行左旋转然后再右旋转
if balance > 1 and self._get_balance_factor(node.left) < 0:
node.left = self._left_rotate(node.left)
return self._right_rotate(node)
# RL 对右节点进行右旋钻然后再左旋转
if balance < -1 and self._get_balance_factor(node.right) > 0:
node.right = self._right_rotate(node.right)
return self._left_rotate(node)
return node
def is_balance(self):
return abs(self._get_balance_factor(self.root)) <= 1
def _right_rotate(self, y):
# 对节点y进行向右旋转操作,返回旋转后新的根节点x,旋转后会改变x、y的高度
# y x
# / \ / \
# x T4 向右旋转 (y) z y
# / \ - - - - - - - -> / \ / \
# z T3 T1 T2 T3 T4
# / \
# T1 T2
x = y.left
temp = x.right
x.right = y
y.left = temp
y.height = 1 + max(self._get_height(y.left), self._get_height(y.right))
x.height = 1 + max(self._get_height(x.left), self._get_height(x.right))
return x
def _left_rotate(self, y):
# 对节点y进行向左旋转操作,返回旋转后新的根节点x 旋转过程中会改变x、y的高度
# y x
# / \ / \
# T1 x 向左旋转 (y) y z
# / \ - - - - - - - -> / \ / \
# T2 z T1 T2 T3 T4
# / \
# T3 T4
x = y.right
temp = x.left
x.left = y
y.right = temp
y.height = 1 + max(self._get_height(y.left), self._get_height(y.right))
x.height = 1 + max(self._get_height(x.left), self._get_height(x.right))
return x
def _get_height(self, node):
# 返回node节点的高度
return node.height if node else 0
def _get_balance_factor(self, node):
# 返回node节点的平衡因子
# node节点的平衡因子,即node节点左右子节点的高度差,设定为左子节点- 右子节点
return self._get_height(node.left) - self._get_height(node.right)
def __contains__(self, item):
return self._contains(self.root, item)
def _contains(self, node, item):
if node == None:
return False
if node.key == item:
return True
if item < node.key:
return self._contains(node.left, item)
else:
return self._contains(node.right, item)
# 返回以node为根的二分搜索树的最小值所在的节点
def mininode(self, node):
if node.left == None:
return node
return self.mininode(node.left)
# 返回以node为根的二分搜索树的最大值所在的节点
def maxinode(self, node):
if node.right == None:
return node
return self.maxinode(node.right)
# 删除掉以node为根的二分搜索树中值为e的节点, 递归算法
# 返回删除节点后新的二分搜索树的根
def _remove(self, node, key):
if not node:
return None
if node.key > key:
# 在左子树查找
node.left = self._remove(node.left, key)
retnode = node
elif node.key < key:
node.right = self._remove(node.right, key)
retnode = node
else:
# 找到了要删除的节点node 现在找后继节点
# 后继节点可以是左子树的最大节点,也可以是右子树最小节点
# 先考虑只有一边节点的情况
if node.left == None:
self.count -= 1
retnode = node.right
node.right = None
elif node.right == None:
self.count -= 1
retnode = node.left
node.left = None
else:
retnode = self.mininode(node.right)
retnode.right = self._remove(node.right, retnode.key)
retnode.left = node.left
node.right = node.left = None
if not retnode:
return None
# 更新node的height
retnode.height = 1 + max(self._get_height(retnode.left), self._get_height(retnode.right))
# 判断是否平衡
balance = self._get_balance_factor(retnode)
# 不平衡条件 balance > 1 或者 balance < -1 代表做右子节点高度差大于1
if balance > 1 and self._get_balance_factor(retnode.left) >= 0:
return self._right_rotate(retnode)
if balance < -1 and self._get_balance_factor(retnode.right) <= 0:
return self._left_rotate(retnode)
if balance > 1 and self._get_balance_factor(retnode.left) < 0:
retnode.left = self._left_rotate(retnode.left)
return self._right_rotate(retnode)
if balance < -1 and self._get_balance_factor(retnode.right) > 0:
retnode.right = self._right_rotate(retnode.right)
return self._left_rotate(retnode)
return retnode
# 删除指定val的节点
def remove(self, key):
self.root = self._remove(self.root, key)




