数据结构——二叉搜索树
上次写的栈和队列还是一个多月前,鸽了这么久终于自觉要回来把数据结构写下去。。
一、二叉搜索树简简介
前几篇文章介绍了主要的几种线性结构,本篇开始进入树(tree)结构。
树结构是由n(n>0)个有限节点组成一个具有层次关系的集合。把它叫做“树”是因为它看起来像一棵倒挂的树,也就是说它是根朝上,而叶朝下的。
它具有以下的特点:
- 每个节点都只有有限个子节点或无子节点;
- 没有父节点的节点称为根节点;
- 每一个非根节点有且只有一个父节点;
- 除了根节点外,每个子节点可以分为多个不相交的子树;
- 树里面没有环路(cycle)

看完树结构的定义,其实就发现了前面我们介绍过的链表也可以归为一种树结构,归纳的来说链表是一种任何节点只有一个或者没有子节点的“单一树”
本文介绍树结构中最常见的一种树,二叉搜索树(Binary Search Tree)
首先介绍几组定义
1.二叉树(Binary tree)是每个节点最多只有两个分支(即不存在分支度大于2的节点)的树结构。通常分支被称作“左子树”或“右子树”。二叉树的分支具有左右次序,不能随意颠倒。

2.完全二叉树是二叉树的一种形态,一棵二叉树中,除最后一层外,若其余层都是满的,并且最后一层或者是满的,或者是在右边缺少连续若干节点,则此二叉树为完全二叉树(Complete Binary Tree)。
3.满二叉树。一棵深度为k,且有2^k-1个节点的二叉树,称为满二叉树(Full Binary Tree)。这种树的特点是每一层上的节点数都是最大节点数。
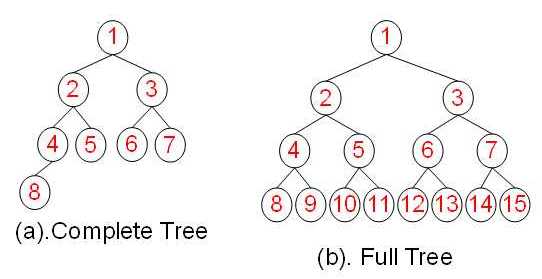
理解了二叉树后来看一看二叉搜索树的定义
二叉查找树(英语:Binary Search Tree),也称为二叉搜索树、有序二叉树(ordered binary tree)或排序二叉树(sorted binary tree),是指一棵空树或者具有下列性质的二叉树:
- 若任意节点的左子树不空,则左子树上所有节点的值均小于它的根节点的值;
- 若任意节点的右子树不空,则右子树上所有节点的值均大于它的根节点的值;
- 任意节点的左、右子树也分别为二叉查找树;
- 没有键值相等的节点。

定义写的很严谨,总结一句话就是任一节点的值a,其左子节点值b,右子节点值c,总会满足c>a>b(假如bc存在的情况,如果不存在,也会部分满足上述不等式)
二、实现分析
从结构上看一棵二叉树每个节点都会有左右子节点,当然也会存储该节点的值,因此我们需要定义一个节点类。
class Node: def __init__(self, val): self.val = val self.left = self.right = None
class Node<T> where T : IComparable { public T Val { get; set; } public Node<T> Left { get; set; } public Node<T> Right { get; set; } public Node(T item) { Val = item; Left = null; Right = null; }
是不是和我们之前写的链表节点十分相似,区别只是维护left、right两个子节点
有了节点,我们开始思考如何给一颗二叉搜索树增加一个节点,增加节点的本质问题在于我们要在树的哪个位置增加,有2种情况:
1.二叉搜素树是一颗空树,这种情况直接让根节点等于我们新增的节点
2.二叉搜索树不是空树,根据左子节点值<节点值<右子节点值的定义,我们需要比较新增节点值和二叉树值,具体来说就是首先比较根节点值是否大于新节点值,如果大于则表示新节点应该在根节点的左子树,然后继续比较根节点的左子节点值与新节点值的大小,不断循环这个过程最后确定新节点的位置,反之亦然。从这个思路来看,我们能很直观的感受到递归的影子,是的树结构是一种天然适合递归的数据结构,我们在后面写的所有实现代码都会基于递归,当然你也可以用迭代去实现。
有了新增节点,那删除节点也不能少,删除一个节点的关键在于如何找到这个节点的位置,其实寻找节点位置的思路和新增节点十分相似,这里我就不继续赘述了。找到要删除的节点以及该节点的父节点后,我们需要重新绑定父节点下的子节点,这个问题稍微有点复杂,我们在后面的实现代码拆开分析讲解。
树的大小(节点数),这个简单,我们维护一个变量count,每次新增节点加一,反之则减一
修改,对于二叉搜索树一般不会存在修改的需求,本文就不涉及了
三、代码实现
定义一个二叉搜索树类BST
class BST: def __init__(self): self.root = None self.count = 0
class BST { private Node<int> root; private int count; public BST() { root = null; count = 0; } ··· }
类中维护根节点root和节点数量count
3.1 增加一个节点
在第二节的分析中,我们使用递归来实现增加节点,定义一个递归函数_add
def _add(val, node): """递归函数 :param val: 新节点值 :param node: 当前节点 :return: 插入节点后的树 """
首先需要判断node是否为空,如果为空我们则直接return一个新Node对象
if node == None: self.count += 1 # 别忘记维护节点数了哦 return Node(val)
如果node不为空,则比较val和node.val,如果val<node.val,则递归进入node的左子树,否则递归进入node右子树
if val == node.val: # 添加重复元素 什么也不干 直接返回原节点 return node if val < node.val: node.left = self._add(val, node.left) else: node.right = self._add(val, node.right)
最后记得要返回node,_add函数完整代码
def _add(val, node): """递归函数 :param val: 新节点值 :param node: 当前节点 :return: 插入节点后的树 """ if node == None: self.count += 1 return Node(val) if val == node.val: # 添加重复元素 什么也不干 直接返回原节点 return node if val < node.val: node.left = self._add(val, node.left) else: node.right = self._add(val, node.right) return node
有了递归函数,我们直接写一个对用户开放的接口函数,add就可以啦
def add(self, val): self.root = _add(val, self.root)
增加节点大功告成!
public void Add(int val) { // 添加一个元素 Node<int> add(Node<int> node, int val) { // 递归函数 if (node == null) { count++; return new Node<int>(val); } if (val.Equals(node.Val)) { return node; } if (val > node.Val) { node.Right = add(node.Right, val); } else { node.Left = add(node.Left, val); } return node; } root = add(root, val); }
3.2 获取树中的最大值
最大值有两层含义,拿到最大值这个val,也需要拿到最大值所在的节点node
实现两个函数
def maxnode(self, node): # 递归返回以node为根的二分搜索树的最大值所在的节点 if node.right == None: return node return self.mininode(node.right) def max(self): # 返回二分搜索树的最大值 node = self.maxnode(self.root) return node.val
使用递归思路实现十分简单,这两个函数会在后面删除节点时用上
private Node<int> MaxNode(Node<int> node) { if (node.Right == null) return node; return MaxNode(node.Right); } public int Max() { return MaxNode(root).Val; }
3.3 删除一个节点
删除节点一个关键点在于,我们把这个节点删除后,它的左右子树如何处理。
情况一:假如该节点只有一个子树或者没有子树,十分好办,假如没有左子树,我们就把它的右子树抓出来顶替它的位置,如果没有右子树,那就抓左子树出来顶替,如果都没有怎么办?不用管,按前面的逻辑我们在判断它没有哪颗树的时候就已经把另外一棵树抓出来了,没有子树代表它返回的是一个None,None也可以认为是一棵树,一颗空树。
情况二:假设该节点左右子树都存在,我们想要找一个节点(后继节点)出来顶替被删除的节点出来就不是那么直观了。回想二叉搜索树的定义,一个节点的左子树下的所有节点会比它小,它的右子树下的所有节点都会比它大。那么我们可以推断,最接近该节点值的2个节点的位置,将会分别位于左子树最右下角的节点(其实也是左子树的最大值节点)和右子树最左下角的节点(也就是右子树的最小值节点),我们把这两个节点任意拎一个出来取代被删除的节点,都不会破坏二叉搜索树的条件。由此,我们这里使用左子树下的最大值节点来替代被删除的节点(也就是3.2函数的作用啦)
情况二中我们找到后继节点后要把它从原位置删除,由于我们这里选择左子树的最大节点作为后继节点,所以先实现一个删除最大节点的功能
def removeMaxNode(self, node): # 删除node节点下的最大节点 if node.right == None: leftright = node.left self.count -= 1 return leftright node.right = self.removeMaxNode(node.right) return node
有了它后我们正式开始写remove函数
def remove(self, val): def _remove(node, val): '''递归函数 :param node: 当前节点 :param val: 删除值 :return: 船新节点 ''' if node == None: # 已经找不到啦 返回None吧 return None if node.val > val: # 递归调用 在左子树查找 node.left = self._remove(node.left, val) return node elif node.val < val: # 递归调用 在右子树查找 node.right = self._remove(node.right, val) return node else: # 找到了要删除的节点node 现在找后继节点 # 后继节点可以是左子树的最大节点,也可以是右子树最小节点 # 先考虑只有一边节点的情况 if node.left == None: self.count -= 1 return node.right if node.right == None: self.count -= 1 return node.left # 找到左子树下的最大节点 successors = self.maxnode(node.left) # 从左子树中删除这个后继节点 node.left = self.removeMaxNode(node.left) # 引用原node左右子树 successors.left = node.left successors.right = node.right return successors self.root = _remove(self.root, val)
我想注释已经写的十分明白了,特别说明一个细节,在递归函数_remove中,node左右节点都存在的情况下我并没有维护count变量自减1,这是因为后面调用的removeMaxNode中已经减少过一次了,所以这里就不用重复减了
至此,这个二叉搜索树已经实现预订目标了
private Node<int> RemoveMaxNode(Node<int> node) { if (node.Right == null) { Node<int> leftNode = node.Left; count--; return leftNode; } node.Right = RemoveMaxNode(node.Right); return node; } public void Remove(int val) { Node<int> removeNode(Node<int> node, int val) { if (node == null) return null; if (node.Val > val) { node.Left = removeNode(node.Left, val); return node; } else if(node.Val < val) { node.Right = removeNode(node.Right, val); return node; } else { if (node.Left == null) { count--; return node.Right; } if (node.Right == null) { count--; return node.Left; } Node<int> successors = MaxNode(node.Left); node.Left = RemoveMaxNode(node.Left); successors.Left = node.Left; successors.Right = node.Right; return successors; } } removeNode(root, val); }
四、复杂度分析
对于一个增加和删除操作,它的时间复杂度都和元素总数无关,只和树的高度相关,与线性结构不同,它不需要去比较每一个元素,每比较一次后会选择左子树或右子树比较,在无序集合的情况下,它的时间复杂度为Olog(n),性能比线性结构O(n)高出不少。
值得一提的是,如果集合有序,那么在最差情况下二叉搜索树会退化为一个单链表。
五、其他
二分搜索树是树中很基础的一种结构,它是很多著名树结构的基础,如avl树、红黑树等。二叉查找树相比于其他数据结构的优势在于查找、插入的时间复杂度较低,遍历一个二分搜索树有前序遍历、中序遍历、后续遍历、层级遍历等方法,使用中序遍历可以得到一个有序序列,而且实现十分简单,感兴趣的同学可以查找这几种遍历方式的定义去亲自实现,附上一份C#中序遍历代码参考(别问为什么没有Python,问就是懒!)
public void InOrder() { //中序遍历打印值 static void _Print(Node<int> node) { if (node == null) return; _Print(node.Left); Console.WriteLine(node.Val.ToString()); _Print(node.Right); } _Print(root); }


