数据结构——链表

1.什么是链表

 链表是一种物理存储结构上非连续、非顺序的存储结构，数据元素的逻辑顺序是通过链表中的指针链接次序实现的。

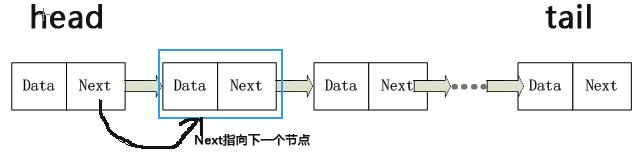
2.节点

节点维护变量data和next，分别用于存储数据和指向下一个节点。

C#:

class Node<T>
{
    private T data;
    private Node<T> next;

    public T Data
    {
        get { return data; }
        set { data = value; }
    }

    public Node<T> Next
    {
        get { return next; }
        set { next = value; }
    }

    public Node(T item)
    {
        data = item;
    }

    public Node(T item, Node<T> nextNode)
    {
        data = item;
        next = nextNode;
    }
}

 Python:

class Node:
    def __init__(self, data, next=None):
        self.data = data
        self.next = next

    def __repr__(self):
        return str(self.data)

3.链表类

正式构建一个链表类

链表类应该具有以下属性或方法：

count	元素数量
head	头节点指针
insert	向指定位置插入元素
get/set	获取/修改节点值
remove	删除指定元素

 

定义好一个类：

C#:

class LinkList<T>:
{
    private Node<T> head;//头节点
    private int count;//计数器
}

Python:

class LinkList:
    def __init__(self):
        self._head = None
        self.count = 0

3.1 获取链表元素个数

由于我们维护了一个属性，所以直接返回count即可

class LinkList<T>:
{
    ...
    public int Count { get { return count; } }
}

在Python中我们重写__len__方法

def __len__(self):
    return self.count

3.2 获取指定位置节点

类比索引功能，设定头节点位置为0，下一节点位置+1

实现一个函数，返回指定位置的Node对象，两种直观解决思路：

迭代，通过一个while或循环来遍历至指定位置

递归，链表是一种天然适合递归的数据结构，通过递归也可以轻松找到目标节点

C#（迭代实现）：

    private Node<T> GetIndexNode(int index)
    {
        //获取指定索引的Node对象
        if (index > count)
        {
            throw new IndexOutOfRangeException();
        }

        Node<T> target = head;
        for (int i = 0; i < index; i++)
        {
            target = target.Next;
        }

        return target;
    }

Python（递归实现）：

def _getnode(self, index: int):
    # 返回指定索引的节点
    def getnode(node: Node, offset: int):
        '''递归函数
        :param node: 节点
        :param offset: 偏移量
        :return:
        '''
        if not node or offset < 0:
            raise IndexError('超出索引范围')
        if offset == 0:
            return node
        return getnode(node.next, offset-1)
    return getnode(self._head, index)

 Tips:使用递归实现可能会出现栈溢出，python默认调用栈容量1000

3.3 向指定位置插入一个节点

向位置i插入一个节点，只要找到目标位置前一个节点(i-1)，把i-1节点的next指向新节点，再把新节点的next节点指向i+1节点即可

特别要注意如果向0位置插入节点，要修改head的指向

C#：

    public void Insert(T item, int i)
    {
        if (i == 0)
        {
            Node<T> newNode = new Node<T>(item,head);
            head = newNode;
        }
        else
        {
            Node<T> preNode = GetIndexNode(i - 1);
            Node<T> newNode = new Node<T>(item, GetIndexNode(i));
            preNode.Next = newNode;
        }

        count++;
    }

Python：

def insert(self, item, index):
    if index > self.size:
        raise IndexError
    if index == 0:
        node = Node(item, self._head)
        self._head = node
    else:
        prev = self._getnode(index - 1)
        node = Node(item, prev.next)
        prev.next = node
    self.count += 1

3.4 访问/修改一个节点的值

前面已经实现了查找节点的访问，现在只用提供一个接口get/set节点存储的值即可

C#：

public T GetItem(int i) {  return GetIndexNode.Data; }

Python：

def __getitem__(self, item):
    if not isinstance(item,int):
        raise IndexError
    return self._getnode(item).data

def __setitem__(self, key, value):
    if not isinstance(key,int):
        raise IndexError
    node = self._getnode(key)
    node.data = value

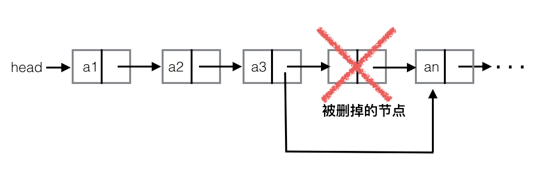
3.5 删除节点

实现pop和remove两个方案，分别使用索引位置和节点值来删除一个节点

C#：

    public T Pop(int i)
    {

        if (i == 0)
        {
            Node<T> target = head;
            head = target.Next;
            count--;
            return target.Data;
        }

        T response = GetIndexNode(i).Data;
        Node<T> preNode = GetIndexNode(i - 1);
        Node<T> nextNode = GetIndexNode(i).Next;
        preNode.Next = nextNode;
        count--;
        return response;
    }

    public void Remove(T item)
    {
        if (head.data = item) {
            head = head.next;
        } else {
            Node<T> prev = Node(None,head);
            while (prev.next != None) {
                Node<T> cur = prev.next;
                if (cur.data == item) {
                    prev.next = cur.next;
                    break;
                }
            }
        count--;
    }

Python：

def pop(self, index: int):
    # 根据索引位置删除链表节点
    prev = self._getnode(index - 1)
    target = prev.next
    prev.next = target.next
    self.count -= 1
    return target.data

def remove(self, item):
    # 根据节点值删除链表节点
    prev = Node(None, self._head)
    while prev.next != None:
        if prev.next.data == item:
            self.count -= 1
            prev.next = prev.next.next
            return
        prev = prev.next

4 性能分析和优化思路

实际上，我们实现的增删改查大多基于GetIndexNode方法，时间复杂度随元素的位置而定，如果操作在链表头，那么时间复杂度O(1)，如果操作在链表尾，时间复杂度则O(n)，整体来看增删改查的时间复杂度均为O(n)。

与数组对比，由于数组是一个在内存连续存放的数据结构，所以数组支持随机访问（任意索引访问时间复杂度均为O(1)）。在随机读写性能上数组会比链表有更好的表现，但是链表也有优点，链表是一个实现了自动扩容的数据结构，我们完全可以不去关心一个链表能容纳多少元素，而数组则往往来通过扩容来实现动态数组，也会造成空间和时间的浪费。

实际上，链表一般只在尾部添加元素，我们完全可以再维护一个foot变量指向链表尾来优化效率。

5. 其他

上面我们实现了一个最基础的链表，实际上链表有不同的许多形式，还有双向链表、循环链表等等，这些链表都是基于单向链表发展出来的，有兴趣的朋友可以亲自一一实现。