数论同余专题总结 - Lazycal

数论同余专题总结

花了一周十分没效率的做了数论同余的专题的基础，还有好多不会啊。先写下来，备忘一下。

以下大部分都是膜拜AC大神(福州大学陈鸿 AekdyCoin)的课件学来的。

基础

1.a = b (mod c) <==> a = cx + b

2.ad = bd (mod cd) <==> ad = cdx + bd <==> a = cx +b <==> a = b (mod c)

即ad = bd (mod cd) <==> a = b (mod c)

3.若(x,c) = 1 且 ax = bx (mod c) 则 a = b (mod c)(由定义可得)

　　推论：

　　　　定义{a1,a2,a3,...,aφ(n)}为模n下的所有与n互质的数组成的集合。

　　　　　当(a,n) = 1时，

a1 * a2 * ... * aφ(n) =

(a*a1) * (a*a2) *... *(a*aφ(n)) =

a^(φ(n)) * a1 * a2 * ... * aφ(n)

　　　　　=>a^(φ(n)) = 1 (mod n)

　　　　　（参考维基百科）

这就是传说中的欧拉定理！

拓展欧几里得

对于ax + by = (a,b) 肯定能找到多组整数解(x,y)

而通过拓展欧几里得可以快速求出一组特解O(log n)

令方程Ax + 0*y = A的解为(1,0)
可以推出原方程的解:
已知上一层的方程:
　　Bx' + (A - A/B * B)y' = (A,B) 的解(x',y')
推出当前层:
　　Ax + By = (A,B) 的解 (x,y)

推导如下:

Bx' + (A - A/B * B)y' = (A,B)
Ay' + (x' - A/B * y')B = (A,B)
对比
Ax + By = (A,B)
可以构造出(x,y) = (y',x' - A/B * y')

通过拓展欧几里得就可以求出

ax + by = (a,b) 的一组特解(x0,y0)

通解如下:

　　x = x0 + b/(a,b)

　　y = y0 - a/(a,b)

对于一般二元一次方程 ax + by = c,

如果(a,b)|c，则只要将原来的解乘上c/(a,b)即可

否则无解。

代码如下:

struct triple
{
	LL x,y,g;
	triple(const LL _x = 0,const LL _y = 0,const LL _g = 0):
		x(_x),y(_y),g(_g){}
};
triple exgcd(const LL a,const LL b)
{
	if (!b) return triple(1,0,a);
	const triple last(exgcd(b,a%b));
	return triple(last.y,last.x - a/b * last.y,last.g);
}

乘法逆元

对于(a,c) = 1，ax = 1(mod c) 则称x是a的乘法逆元。

b/a = bx (mod c)

模上除法

当a | b时，计算 a/b % p (p为任意整数)

1.对于b存在关于p的逆元x

则a/b % p = a*x % p

2.不存在逆元

　　记下a和b中与能整除p的质因子的次数，剩下的就有逆元了。

当a 不整除 b时，计算[a/b] % p：

令 c = a % b,则

[a/b] % p = (a - c)/b % p = ((a - c) % (p*b)) / b （参考http://hi.baidu.com/aekdycoin/item/11ae3c86d22a3d18c31627d4）

线性模方程组

对于如下方程组:

x = r1 (mod a1)

x = r2 (mod a2)

...

x = rn (mod an)

（如果x前面有系数，如果系数与模数不互质，先除掉，直到互质，然后乘上乘法逆元就可以转换成上面的样子）

先处理两个，然后合并，再与第三个做。

x = r1 (mod a1)

x = r2 (mod a2)

x = a1 * y + r1 = a2 * z + r2

解出y

然后合并 x = a1 * y + r1 (mod lcm(a1,a2))

---------------------------------------------------------------------------------------

特别的，如果(a1,a2,...,an) = 1，则可以用中国剩余定理求解，优点是常数小，代码短

中国剩余定理的做法是一次性得出解：

基本思路是构造一个数:b1 * r1 + b2 * r2 + b3 * r3 +.... + bn * rn

满足bi % ai = 1 bi % aj = 0(j != i)

令Mi = a1 * ... * an / ai

构造方法是令p,q为方程Mi * p - ai * q = 1

则bi = Mi * p.

而且在区间[0,a1 * a2 * ... * an]中只有一个解。证明可以通过第一种方法的求解方法推出。

代码：

long long CRT(const long long (&a)[100],const long long (&r)[100],const long long cnt)
{
    long long res = 0,MM = 1;
    for (long long i = 1; i <= cnt; ++i) MM *= a[i];
    for (long long i = 1; i <= cnt; ++i)
        (res += exgcd(MM / a[i],a[i]).x % a[i] * r[i] % MM * (MM / a[i]) % MM) %= MM;
    return (res + MM) % MM;
}

阶乘取模分解

任务：将n! 在mod p^c下分解成 p^a* b (p^c <= 10^5,n <= 10^9)

n! =  
      1 *      2  * ... *  (p - 1) *                                  p *
(p + 1) * (p + 2) * ... * (2p - 1) *                                 2p *
...
((p^(c - 1) - 1) * p + 1) * ... * (p^(c - 1) * p - 1) * (p^(c - 1) * p) *
      1 *      2  * ... *  (p - 1) *              ((p^(c - 1) + 1) * p) *
(p + 1) * (p + 2) * ... * (2p - 1) *              ((p^(c - 1) + 2) * p) *
...
可以发现，存在循环节，后面则是p^(n/p) * (n/p)!
举个例子：
　　（参考http://hi.baidu.com/aekdycoin/item/e051d6616ce60294c5d249d7）
　　令n = 19,p = 3,c = 2.即求n! % 9
　　n! = 1 * 2 * 3 * ... * 19
　　   = [1 * 2 * 4 * 5 * 7 * 8] * [10 * 11 * 13 * 14 * 16 * 17] * 19 * (3 * 6 * 9 * 12 * 15 * 18)
　　   = [1 * 2 * 4 * 5 * 7 * 8]^2 * [19] * 3^6 * (1 * 2 * 3 * 4 * 5 * 6)
   后面的一坨是p^(n/p) * (n/p)!,前面的就是fac[p^c - 1]^(n / p^c) * fac[n % p^c]

代码：

typedef std::pair<long long,long long> Pair;
Pair FnModP(long long n,const long long p,const long long MOD)
{
    //Fn = n!
    //fac[n] = n! % p
    //n! = p^res.first * res.second (mod p^c)
    long long res = 1; long long c = 0;
    while (n) {
        (res *= power(fac[MOD],n / MOD,MOD)) %= MOD;
        (res *= fac[n % MOD]) %= MOD;
        n /= p;
        c += n;
    }
    return std::make_pair(c,res);
}

欧拉函数

定义φ(n) = 1到n中与n互质的数的个数。

有如下性质：

（1）若p是素数，E(p)=p-1。
（2）E(p^k)=p^k-p^(k-1)=(p-1)*P^(k-1)

（3）若ab互质，则E(a*b)=E(a)*E(b)，欧拉函数是积性函数.

（4）φ(n) = n*(1-1/p1)*(1-1/p2)*…*(1-1/pk)

线性筛法求欧拉函数：

for (int i = 2; i <= 1000000; ++i) {
	if (!mark[i]) {
		p[++p[0]] = i;
		E[i] = i - 1;
	}
	for (int j = 1; j <= p[0] && 1ll * p[j] * i <= 1000000; ++j) {
		mark[i * p[j]] = true;
		if (i % p[j] == 0) {
			E[i * p[j]] = E[i] * p[j];
			break;
		}else E[i * p[j]] = E[i] * (p[j] - 1);
	}
}

log(n)求phi(n)

LL getphi(LL x)
{
	LL res = 1;
	for (LL i = 2; i * i <= x; ++i)
		if (x % i == 0) {
			x /= i;
			res *= i - 1;
			while (x % i == 0) x /= i,res *= i;
		}
	if (x > 1) res *= x - 1;
	return res;
}

求幂大法

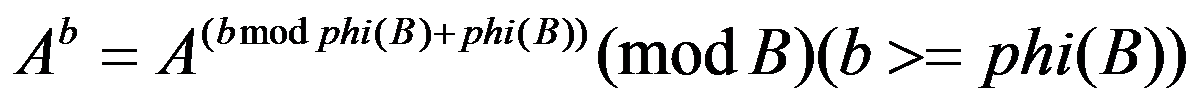
（这个定理的名字和历史渊源暂时未知……第一次是在AC大神的课件上看到的）

AC大神的空间也有证明，不过我看不懂……

这里贴一个比较简单的证明，是某位大神自己推导的，而且自己得出了上述定理(orz)。传送门。

大体思路就是通过证明当A是p^c时成立推出原式成立（p为素数）:

p^s = p^(s + len) (mod B)

B|(p^s * (p^len - 1))

令B = p^s0 * B'

则s = s0,B' | (p^len - 1)

p^len = 1 (mod B')

len | phi(B') | phi(B)

----------------------------------------------------------------------------------------

这里A必须是整数！

如果A是矩阵或者浮点数都是不行的，除非可以被整体代换。（如hdu3802）

循环节

对于函数f[i] = f[i - 1] * a % p,其中a是常量，p为任意整数，是存在循环节的。

不过起点不一定是1.若要满足起点是1，则必须a有关于p的逆元，即可以逆推。

对于f[i] = a^i的讨论可以参考求幂大法。

组合数取模

求解C(n,m) % p：

n,m <= 1000000:随便暴搞，例如拆分出所有质因数，或者拆出p的倍数。

p <= 1000000: 当p是素数时，可以用lucas定理:C(n,m) = C(n/p,m/p)*C(n%p,m%p)%p.证明。

若p不是素数，拆成mod pi^ci，最后再合并。

对于C(n,m) % p^c，可以用阶乘取模来求解。复杂度O(log(n) + p^c)

代码

long long C(const long long n,const long long K,const long long p,const long long MOD)
{
    //nCK % p^c
    calc_fac(p,MOD);
    Pair a(FnModP(n,p,MOD)),b(FnModP(K,p,MOD)),c(FnModP(n - K,p,MOD));
    return 1ll * power(p,a.first - b.first - c.first,MOD) * a.second % MOD * ((exgcd(1ll * b.second * c.second % MOD,MOD).x % MOD + MOD) % MOD) % MOD;
}

Baby Step Giant Step

求解A^x = B (mod C) 中 0 <= x < C 的解,C 为素数。

运用分块的思想：

令m = √C

x = i * m + j (0 <= i <= m,0 <= j <= m)

先将A^j(0 <= j <= m)的最小j存到hash表里面。

然后枚举i，求A^(i*m) * x = B(mod C)的最小解x是否在hash表里面存在，存在即是解。

（思考：为何不会有其他的在hash表里的但是不是最小解的x？

ax1 = B

ax2 = B

==> x1 = x2 (mod C)矛盾。这也解释了C是素数这一条件的作用。

）

----------------------------------------------------------------------

拓展Baby Step Giant Step

C不为素数。

A^x = B(mod C)

如果可以约(A,C)，就把原式约掉：

A^(x - 1) * A' = B'(mod C')

直到(A,C) = 1,记下次数times.

原式变成 A^x = B'(mod C') (x >= times)即可以用非拓展版求解。注意当x < times时需要特判。

（思考：这货跟循环节好像有点关系……可以发现：非拓展版的A^x % C是存在循环节的，并且从1开始。而拓展版的就不一定(起点是times)，需要进行转化。所以如果要求解的个数，如果是在起点前就有解的，那么最终就只有一个解）

LL BSGS(LL A,LL P,LL D)
{
	LL AA = 1 % P,x = 1 % P,MOD = P,DD = D,m = static_cast<LL>(std::ceil(std::sqrt((double)P)));
	times = 0;
	for (triple tmp; (tmp = exgcd(A,P)).g != 1; ) {
		if (x == DD) return times++;
		if (D % tmp.g) return -1;
		P /= tmp.g;
		D /= tmp.g;
		(AA *= A / tmp.g) %= P;
		++times;
		(x *= A) %= MOD;
	}
	A %= P;
	ec = 0;
	memset(H,0,sizeof H);
	LL tmp = 1 % P;
	for (int i = 0; i < m; ++i,(tmp *= A) %= P)	
		insert(tmp,i);
	x = 1 % P;
	for (LL i = 0; i < m; ++i,(x *= tmp) %= P) {
		const int j = find(rem_equ(AA*x%P,P,D));
		if (j != -1) return i * m + j + times;
	}
	return -1;
}

原根

若整数g满足g^x = 1(mod m) 的最小x是phi(m),则称g是m的原根。

模 $m$ 有原根的充要条件是 $m = 1 , 2 , 4 , p^n , 2p^n$ ，其中 $p$ 是奇质数， $n$ 是任意正整数。

原根有什么用？原根的x次幂可以表示出mod m下的所有与m互质的数。

特别的，当m是素数时，{g^1,g^2,g^3,...,g^(m - 1)}刚好表示出了mod m下的所有数。

如何求？

由于最小的原根很小，所以直接枚举！

二次剩余

x^2 = a(mod p)

（以下只研究p为素数）

若有解，则a是p的二次剩余，否则为p的二次非剩余。

令x = g^y 则

a = x^2 = g^2y

<==>

a^((p-1)/2) = g^(p - 1) = 1 (mod p)

所以若a^((p-1)/2) = 1 (mod p) 则肯定有解。

否则 a = g^(2y + 1)

a^((p-1)/2) = g^((p-1)/2) = -1 (mod p) (思考：为何是-1？)

高次方程

x^a = b( mod c)

c是素数

x = g^y（g是原根）

x^a = g^ay = b (mod c)

这个可以用BSGS求.

就这些了吧……其他的就不会了……

例题就是AC大神里面的那些例题了……那些我会另写题解。

posted on 2013-10-21 11:54 Lazycal 阅读(1597) 评论(0) 编辑收藏举报

刷新页面返回顶部

基础

拓展欧几里得

乘法逆元

模上除法

线性模方程组

阶乘取模分解

欧拉函数

求幂大法

循环节

组合数取模

Baby Step Giant Step

原根

二次剩余

高次方程