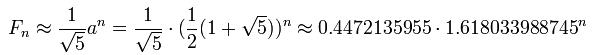Fibonacci数列学习笔记

无意中在网上看到Fibonacci数列的文章，就又重新学习了一把。

这里是来在维基百科上的关于Fibonacci数列的介绍：

在数学上，斐波那契数列是以递归的方法来定义：

  • F0 = 0
  • F1 = 1
  • Fn = Fn - 1 + Fn - 2

用文字来说，就是斐波那契数列由0和1开始，之后的斐波那契数就由之前的两数相加。首几个斐波那契数是（OEIS A000045）：

0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, 2584, 4181, 6765, 10946，………………

特别指出：0不是第一项，而是第零项。

 

关于Fibonacci数列的一些神奇的特性：

 

  • Fibonacci数列可以表示为无限连分数。而黄金分割数也是无限连分数。所以Fibonacci数列的后一个数与前一个数的比是趋向于黄金分割比例的。
  • 向日葵的种子的螺旋排列99%的符合Fibonacci数列的。
  • Fibonacci前n项的和等于F(n+2)-1。
以下内容转载自http://hi.baidu.com/zero239/blog/item/8efcd307280649cc7a8947b0.html
如果你看到有这样一个题目：某人把一个8*8的方格切成四块，拼成一个5*13的长方形，故作惊讶地问你：为什么64＝65？其实就是利用了斐波那契数列的这个性质：5、8、13正是数列中相邻的三项，事实上前后两块的面积确实差1，只不过后面那个图中有一条细长的狭缝，一般人不容易注意到
如图：



如果任意挑两个数为起始，比如5、-2.4，然后两项两项地相加下去，形成5、-2.4、2.6、0.2、2.8、3、5.8、8.8、14.6……等，你将发现随着数列的发展，前后两项之比也越来越逼近黄金分割，且某一项的平方与前后两项之积的差值也交替相差某个值
fibonacci螺旋在生活中也到处都是：

 

面试中关于Fibonacci数列最常见的问题应该就是求第n项的值。在这里列出一些现有的解法：

1、递归 
递归应该是最直观的第一时间会被想到的算法。但是用递归来求Fibonacci第n项的值存在严重的性能问题（递归过程中存在大量重复计算，比如算F(5)的时候会算F(3), 算F(6)也会算F(3)......），算法复杂度为O(2^n)，差不多当n大于46的时候，运算速度就难以让人忍受。 这里给出基于递归的代码：

        private double Fibonacci1Recursive(double data)
        {
            if (data == 0)
            {
                return 0;
            }
            if (data == 1)
            {
                return 1;
            }
            else
            {
                return Fibonacci1Recursive(data - 2) + Fibonacci1Recursive(data - 1);
            }
        } 

2、引入中间变量储存计算结果以进行单层循环

为了解决递归过程中产生的大量重复计算，可以引入中间变量用于保存计算过的结果。这样只需要执行从0到n的循环就可以了，算法负责度为O(n)。以下是范例代码:

        public double Fibonacci2(object inputData)
        {
            int data = (int)inputData;

            double num1=0, num2=0, num3=0,result=0;

            for (int i = 0; i <= data; i++)
            {
                if (i == 0)
                {
                    num1=0;
                    result = num1;
                }
                else if (i== 1)
                {
                    num2 = 1;
                    result = num2;
                }
                else
                {
                    num3 = num1 + num2;
                    num1 = num2;
                    num2 = num3;
                    result = num3;
                }
            }

            return result;
        }

 

 

这样的O(n)的算法在处理相对大一些的数还可以接受，但是在处理一些极大的数时，性能还是不能让人接受。


3、通项公式（初等代数解法）

在面试中，得出这样的结论还不够，面试官还会问有没有效率更高的算法了。一般尝试过直观解法（算法复杂度可能会很高），被一定程度优化的解法（通过一些编程层面的技巧可能能把算法复杂度降到O(N)或O(logN)），还要进一步优化的话，就得上升到数学高度了（初等数学，高等数学，线性代数，离散数学，晕了，少壮不努力，老大写程序）。

实际上可以通过求F(n)的通项公式，使算法复杂度降到O(1)。在这里先给出通项公式，再来谈如果求通项公式。 

公式：

范例代码: 

        public double Fibonacci3(double data)
        {
            return Math.Sqrt(5) / 5 * (Math.Pow((1 + Math.Sqrt(5)) / 2, data) - Math.Pow((1 - Math.Sqrt(5)) / 2, data));
        }

 

 

以下是摘自维基百科的关于通项公式的求法（原来求递归数例的通项公式有好几种方法，以下解法用到的是构造等比数例的方法）:
 

这个通项公式非常奇妙。看上去它好像是一个无理数，但实际上只要n>0，它的值都是整数。。。。。。。。。。
唉，看来这年头，学不好大学数学，是很难写出牛B的代码滴， 

 

4、线性代数解法

线性代数的解法我还没有看懂，在这里就不贴具体内容了。。。。。。

线性代数解法可以推出如下的近似公式：


 

关于Fibonacci数列还有很多值得深入研究的地方，再一次强烈感觉到科学家们真是伟大。。。。。。

 

posted on 2009-12-27 17:17  林大虾  阅读(955)  评论(0)  编辑  收藏  举报

导航