形式化建模与分析方法知识点
这个是比较针对期末复习的知识点整理,根据我的复习随缘更新,如果发现有些部分没写那就是因为我还没复习到(大概)
(PS:这些知识点中有很大部分来自老师的PPT,也有一部分来源于学长学姐整理的资料,最后也有一小部分来源于我自己的总结)
一.简答题
1.串行系统的程序正确性定义。

2.有限状态机的不足之处。(考了,还考了Statecharts优化了有限状态机的哪些不足之处)

3.Moore机的六元组定义

4.Mealy机的六元组定义

记忆方法:Mealy机与Moore机的不同在于λ不同,所以在记忆的时候只需要记住一个,然后再分别记忆λ即可。
5.Statecharts中状态节点的类型。

6.Petri网模型上迁移间的关系(解释+画图)(考了解释和画图)
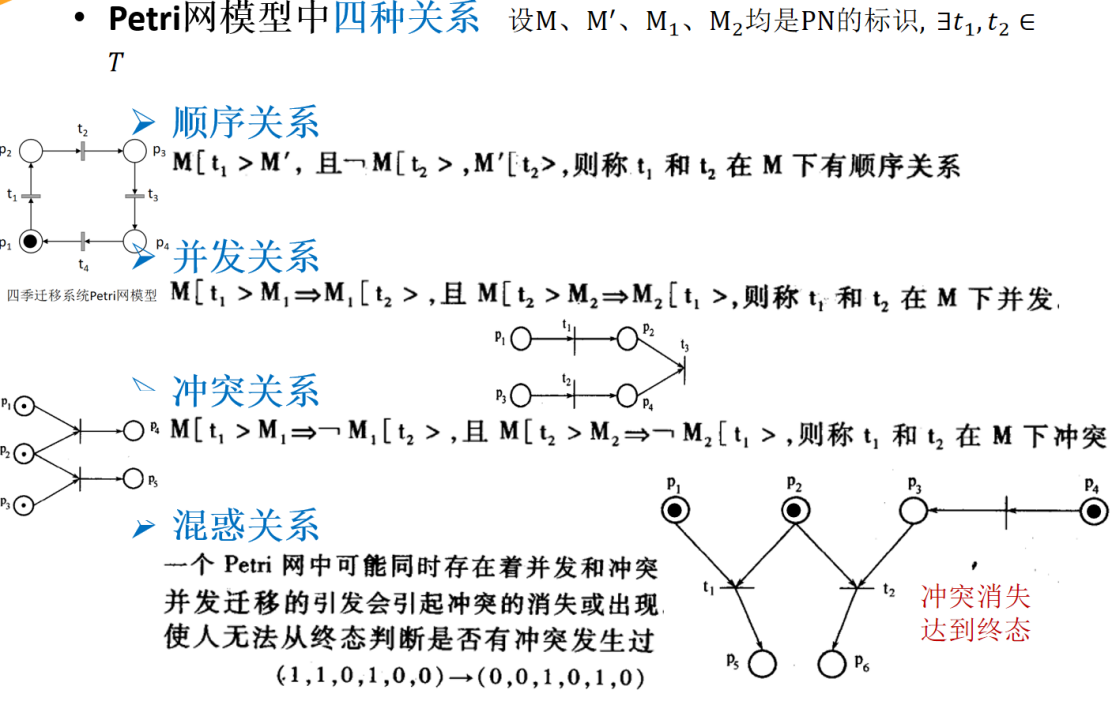
(1)顺序关系:
(2)并发关系:
概念记忆法:
1) M[t1>表示t1引发
2) M[t1>M'表示M随着t1的引发变为M'
死记硬背的记忆方法:可以发现并发和冲突之间的差别就是推出符号后面是否有¬,有¬即为冲突关系,没有则为并发关系,所以如果要强行记下来的话,只需要记住并发状态,然后就可以根据观察到的差别写出冲突关系了。
(3)冲突关系
(4)混惑关系
7.几种特殊Petri网对各类关系的描述能力。
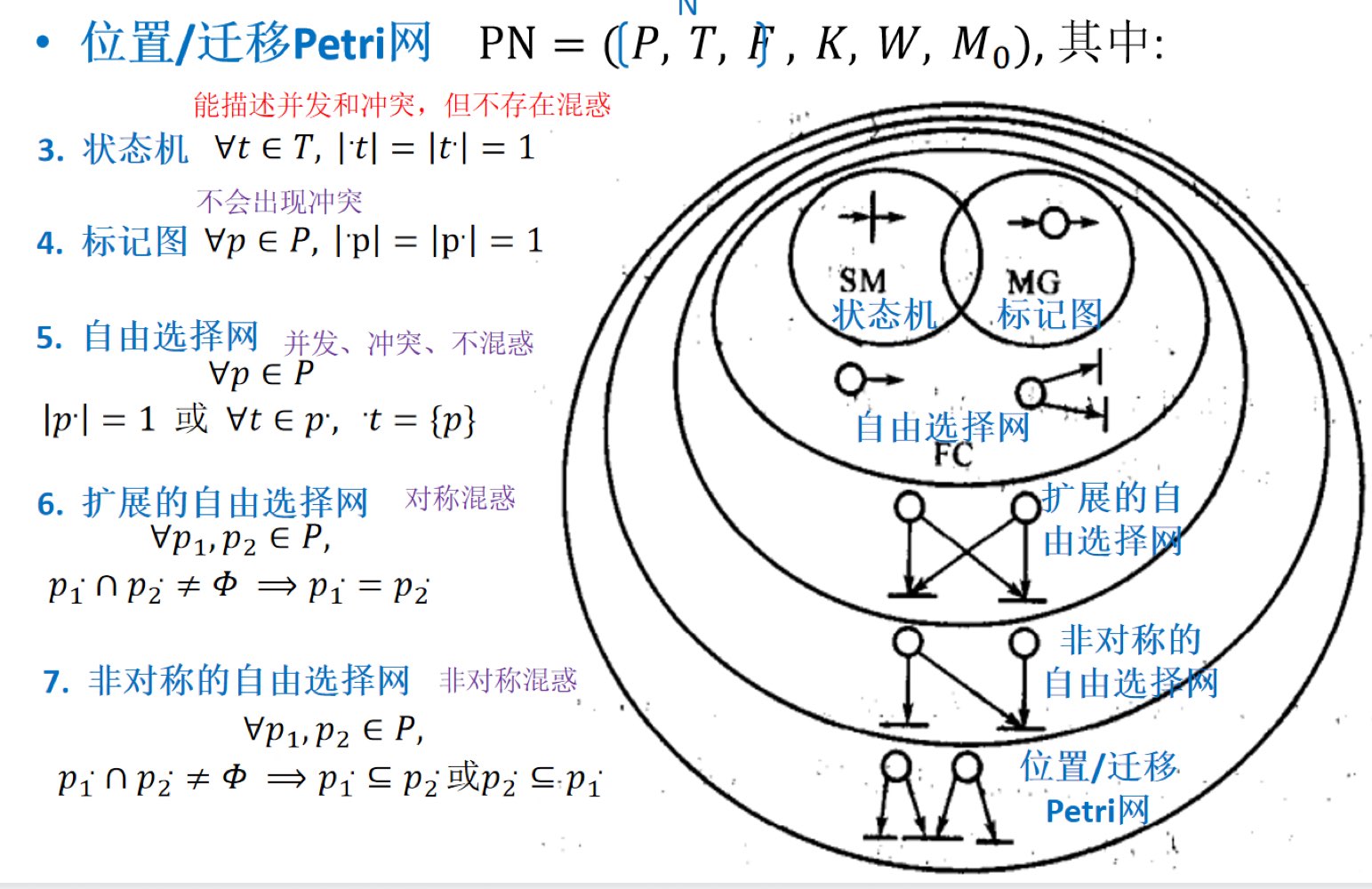
8.Petri网的行为性质(能列出三种并解释含义)
对Petri网PN =(P,T,F,M0) (在特定M0下讨论)
(1)可达性
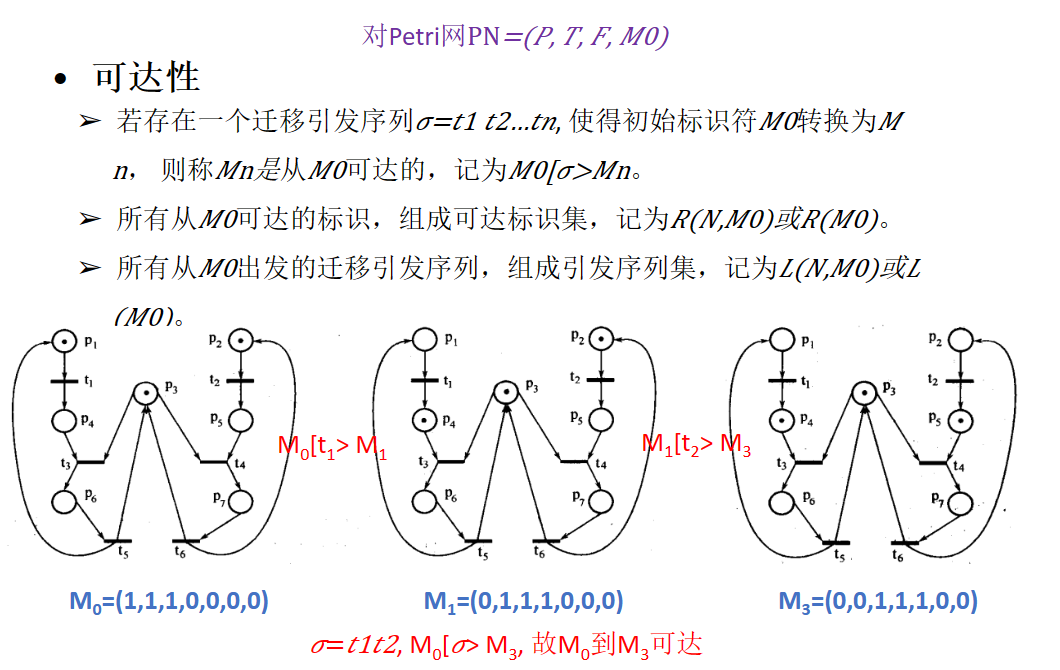
(2)有界性和安全性
(3)活性(以最低级的活性作为整张图的活性)

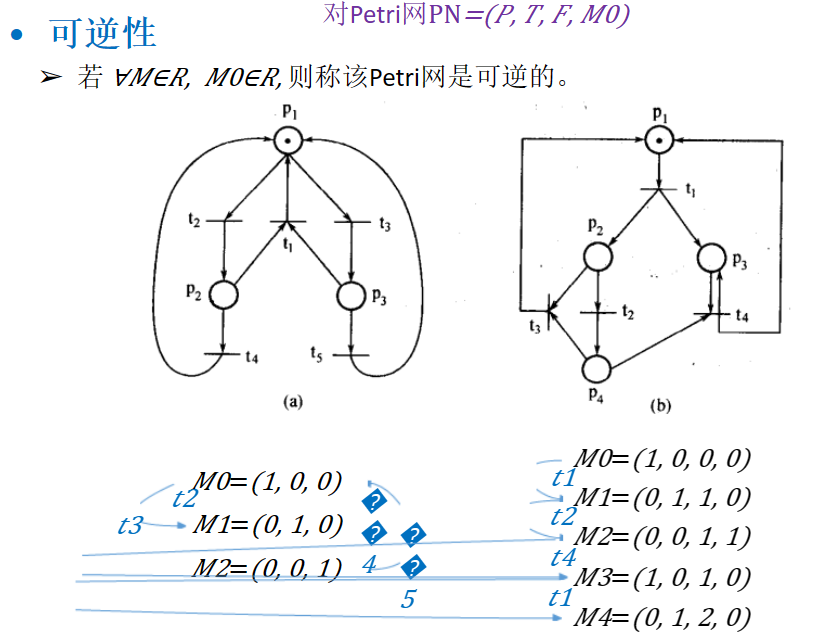
(4)可逆性
简单的可以认为是:从第一个位置P1开始,走了一圈之后回到P1
二.分析证明题
1.Floyd 前后断言法(例5.3.1、例 5.3.2、课后5.7)
(1)归纳断言法 ---- 证明部分正确性(考了归纳断言法,例题5.3.1)
(2)良序集法 ---- 证明终止性
2.Hoare 公理化方法,证明程序部分正确性(例5.3.3、课后5.8(1))
3.Dijstra最弱前置谓词法,证明程序完全正确性(P133下数组求和题、课后5.9)(考了P133下数组求和题)
4.有限状态机:
(1)给出定义形式的一个有限状态机,画出其状态转移图、状态转移表、状态转移矩阵;或给出状态转移图形式的有限状态机,写出其定义形式。(考了根据状态图写出五元组定义形式)
(2)写出有限状态机所接受的语言集合。(考了所接受的语言集合)
5.Petri网:(课后3.1、3.7、3.8)
(1)化简。(考了化简)
Petri网的化简可以通过以下六种方式:
1)消除自循环位置
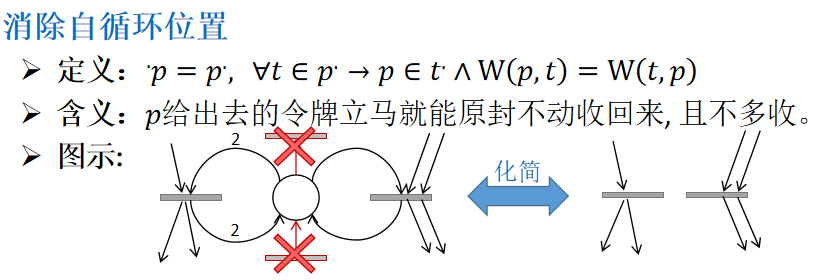
2)消除自循环迁移
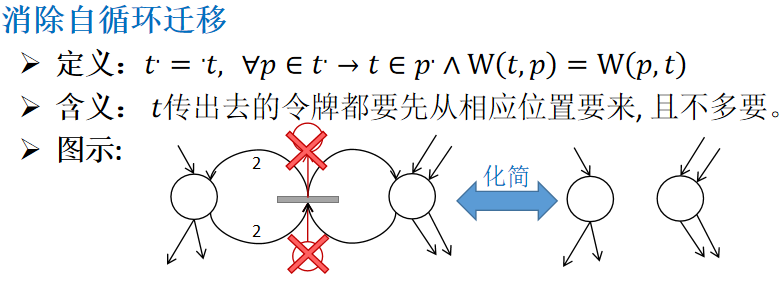
3)合并串行位置
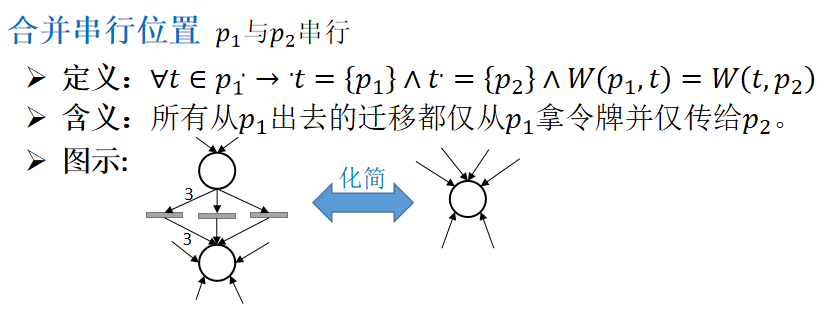
4)合并并行迁移

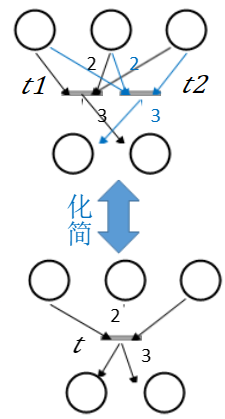
5)合并串行迁移
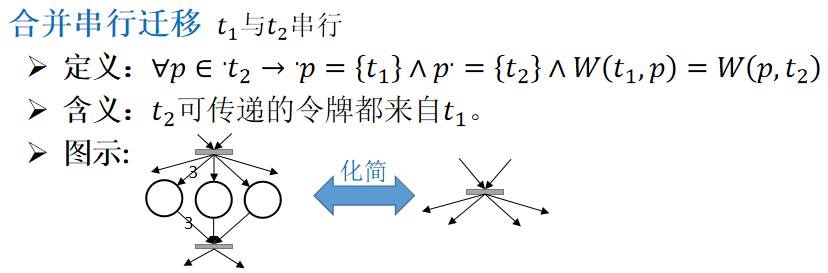
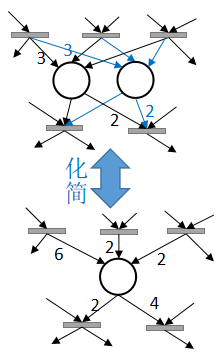
6)合并并行位置

(2)覆盖树生成。(考了)
(3)有界性、活性、可逆性分析。(可结合化简或覆盖树)(考了)
以下是根据覆盖树进行判断:
1)有界性:观察覆盖树,如果每一个位置的M都不全为0且没有ω,那么为有界,否则,如果有个Mi={0,0,ω,0}(存在ω),那么为无界(ω代表无限大)
2)活性:若每一个迁移都引发了,那么为具有活性,如果有迁移未引发,则活性为l0
3)可逆性:如果有Mi与M0一致,则称有可逆性
三.应用题
1.有限状态机(课后2.6、课后2.8)、Moore机(图2.4、课后2.4(1))、Mealy机(图2.5、课后2.4(2))设计。(考了设计,是人、狼、羊、菜过河问题)
(1)有限状态机的五元组定义




