leetcode动态规划题组笔记以及总结(持续更新)
date:20210520
No:1025
title:除数博弈
description:爱丽丝和鲍勃一起玩游戏,他们轮流行动。爱丽丝先手开局。 最初,黑板上有一个数字 N 。在每个玩家的回合,玩家需要执行以下操作: 选出任一 x,满足 0 < x < N 且 N % x == 0 。 用 N - x 替换黑板上的数字 N 。 如果玩家无法执行这些操作,就会输掉游戏。 只有在爱丽丝在游戏中取得胜利时才返回 True,否则返回 False。假设两个玩家都以最佳状态参与游戏。
解题方法:
- 动态规划
- 归纳法
解题思路:
- 动态规划:
- 最后一个数字(即n)的状态和前一个因数的状态有关————(解释:爱丽丝轮到的因数会一步一步导致结果,那么我们倒过来,从前往后推,从爱丽丝轮到因数1和2开始推(因为二者是已知的))
- 保存爱丽丝会轮到所有因数的状态(也就是说保存爱丽丝在每一个因数处的结果,以供下一个因数查询————记忆化查询)
- 归纳法:
- 数学方法,本专题主要记录动态规划,所以在此不赘述其他方法,官方有给题解,可以去leetcode看看
实现代码:
- 本题使用python3:
class Solution:
def divisorGame(self, n: int) -> bool:
target = [0 for i in range(n+1)]
target[1] = 0
if n <= 1:
return False
else:
target[2] = 1 # 若爱丽丝抽到2,则爱丽丝赢
for i in range(3,n+1):#因为(3,n)不包括n所以用n+1
for j in range(1,i//2):
if i%j==0 and target[i-j]==0:
target[i] = 1
return target[n] == 1
- 动态规划法通过截图:
date:20210521
No:剑指offer No.42
title: 连续子数组的最大和
description:输入一个整型数组,数组中的一个或连续多个整数组成一个子数组。求所有子数组的和的最大值。 要求时间复杂度为O(n)。
解题方法:
- 动态规划
- 暴力
解题思路:
- 动态规划:
- 构建动态规划数组,每一个格子记录以当前位置为结尾的最大连续序列的和,然后遍历完之后找dp数组中最大的数字,即为答案
- 暴力:
- 这没啥说的,遍历,以每个位置为结尾在嵌套一个遍历,把所有的可能都列出来,然后找最大的(简略的说了下,主题是动态规划,在此不再赘述)
实现代码:
- 本题使用java:
public int maxSubArray(int[] nums) {
int[] dp = new int[nums.length];
Arrays.fill(dp,Integer.MIN_VALUE);
dp[0] = nums[0];
for(int i = 1;i<nums.length;++i){
dp[i] = Math.max(dp[i-1]+nums[i],nums[i]);
}
int res = Integer.MIN_VALUE;
for (int i : dp) {
res = Math.max(i,res);
}
return res;
}
- 通过截图
date:20210522
No:764
title: 使用最小花费爬楼梯
description:数组的每个下标作为一个阶梯,第 i 个阶梯对应着一个非负数的体力花费值 cost[i](下标从 0 开始)。 每当你爬上一个阶梯你都要花费对应的体力值,一旦支付了相应的体力值,你就可以选择向上爬一个阶梯或者爬两个阶梯。 请你找出达到楼层顶部的最低花费。在开始时,你可以选择从下标为 0 或 1 的元素作为初始阶梯。
解题方法
- 剪枝
- 动态规划
解题思路:
-
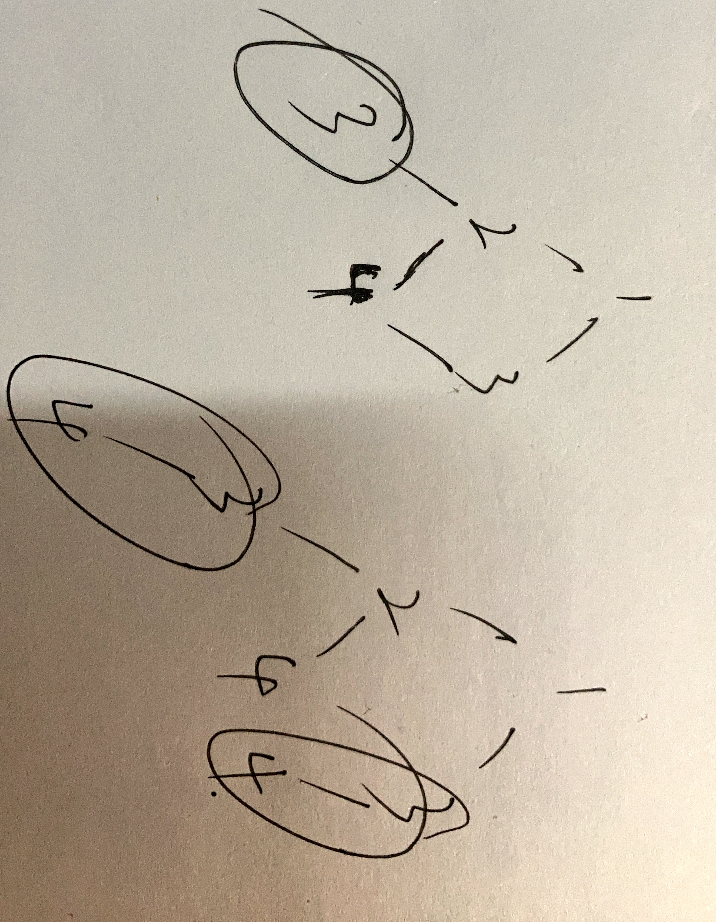
剪枝:通过递归模拟走楼梯,然后计算走一步和走两步的最小值,最后通过一个过渡数组记录经过的点的最优解,防止再次递归到这个点的时候重复计算,走楼梯过程如下图,会有重复的节点树
-
动态规划:动态规划的核心就是记忆化搜索,所以定义一个dp数组,每个格子保存当前到位置的最小消耗,最后返回倒数两个节点中的小值即可
实现代码
- 剪枝:
package algorithm;
import java.util.Arrays;
public class MinCostClimbingStairs {
private static int[] dp;
public static int minCostClimbingStairs(int[] cost) {
dp = new int[cost.length+1];
Arrays.fill(dp,0);
minCostClimbingStairs(cost,-1,dp);
return dp[0];
}
private static int minCostClimbingStairs(int[] cost,int index,int[] dp){
if(index>=cost.length){
return 0;
}
int temp = index ==-1?0:cost[index];
if(dp[index+1]!=0) {
return dp[index+1];
}
int one = minCostClimbingStairs(cost, index + 1, dp);
int two = minCostClimbingStairs(cost, index + 2, dp);
dp[index+1] = Math.min(one + temp, two + temp);
return dp[index+1];
}
public static void main(String[] args) {
int[] cost = {1, 100, 1, 1, 1, 100, 1, 1, 100, 1};
System.out.println(minCostClimbingStairs(cost));
}
}
- 动态规划:
class Solution {
public int minCostClimbingStairs(int[] cost) {
for(int i = 2;i<cost.length;++i){
cost[i] += Math.min(cost[i-1],cost[i-2]);
}
return Math.min(cost[cost.length-1],cost[cost.length-2]);
}
}
通过截图
date:20210523
No:面试题 17.16
title: 按摩师
description:一个有名的按摩师会收到源源不断的预约请求,每个预约都可以选择接或不接。在每次预约服务之间要有休息时间,因此她不能接受相邻的预约。给定一个预约请求序列,替按摩师找到最优的预约集合(总预约时间最长),返回总的分钟数。 注意:本题相对原题稍作改动
解题方法:
- 动态规划
解题思路:
- 动态规划:
- 设计一个dp数组,每一个格子保存以当前位置结尾的最大预约时间(可以不包含当前位置预约),最后返回最后一个格子即可;保存策略就是,对比nums[i]+dp[i-2]和dp[i-1]的大小,保存大的值,一次遍历之后,最后一个格子保存的就是整个序列中最大的预约时间
实现代码
- 本题使用的语言是python3
class Solution:
def massage(self, nums: List[int]) -> int:
if len(nums)<=0: return 0
if len(nums)==1: return nums[0]
dp = []
dp.append(nums[0])
dp.append(max(nums[0],nums[1]))
for i in range(2, len(nums)):
dp.append(max((dp[i-2]+nums[i]),dp[i-1]))
return dp[-1]
通过截图
date:20210524
No:329
title: 判断子序列
description:给定字符串 s 和 t ,判断 s 是否为 t 的子序列。 字符串的一个子序列是原始字符串删除一些(也可以不删除)字符而不改变剩余字符相对位置形成的新字符串。(例如,"ace"是"abcde"的一个子序列,而"aec"不是)。 进阶: 如果有大量输入的 S,称作 S1, S2, ... , Sk 其中 k >= 10亿,你需要依次检查它们是否为 T 的子序列。在这种情况下,你会怎样改变代码?
解题方法:
- 双指针
- 动态规划
解题思路:
- 双指针:在s和t上各安排一个指针,然后遍历t,只要s的对应字符等于t当前位置字符,s的指针加一,如果s的指针到达末尾,则说明s为t的子序列,就返回true,否则如果一个循环都未返还,说明s中有t中不存在的字符,返回false
- 动态规划:还是那句话,动态规划的核心是记忆化搜索,我们只要维护一个二维数组,记录从第i(t上)个字符开始,下一个字符(26个字母)出现的位置,遍历s时查询t就可以线性化,复杂度为O(1),至于dp数组,从后面开始遍历记录就好;
实现代码
- 双指针:
class Solution {
public boolean isSubsequence(String s, String t) {
if(s.equals("")) return true;
if(s.length()>t.length()) return false;
int index_s = 0;
char temp = s.charAt(index_s);
for(int i = 0;i<t.length();++i){
if(temp==t.charAt(i)){
index_s++;
if(index_s==s.length()) return true;
temp = s.charAt(index_s);
}
}
return false;
}
}
- 动态规划:
class Solution {
public boolean isSubsequence(String s, String t) {
if(s.length()>t.length()) return false;
if(s.length()==0)return true;
int n = s.length();
int m = t.length();
int[][] dp = new int[m+1][26];//记录每一个字符开始下一个字符的位置
for (int[] ints : dp) {
Arrays.fill(ints,m);
}
for(int i = m-1;i>=0;--i){
for(int j = 0;j<26;++j){
if(t.charAt(i)==j+'a'){
dp[i][j] = i;//说明该字符在当前位置出现
}else{
dp[i][j] = dp[i+1][j];//继承上一个状态
}
}
}
int next = 0;
for(int i = 0;i<n;++i){
if(dp[next][s.charAt(i)-'a']==m){//说明该字符不会出现
return false;
}else{
next = dp[next][s.charAt(i)-'a']+1;
}
}
return true;
}
}
通过截图
-
双指针:
-
动态规划:
date:20210525
No:1641
title: 统计字典序元音字符串的数目
description:给你一个整数 n,请返回长度为 n 、仅由元音 (a, e, i, o, u) 组成且按 字典序排列 的字符串数量。 字符串 s 按 字典序排列 需要满足:对于所有有效的 i,s[i] 在字母表中的位置总是与 s[i+1] 相同或在 s[i+1] 之前。
解题方法:
- 动态规划
解题思路:
- 还是那句话:动态规划的核心就是记忆化搜索以及实时更新记忆,该题有如下规律(别的博客学来的,我太菜了/大哭):

实现代码:
- 本体使用java语言
class Solution {
public int countVowelStrings(int n) {
int[] dp = {1,1,1,1,1};
for(int i = 1;i<n;++i){
for(int j = 3;j>=0;--j){
dp[j] += dp[j+1];
}
}
int sum = 0;
for (int i : dp) {
sum += i;
}
return sum;
}
}
通过截图:

date:20210528
No:1314
title:矩阵区域和
description:给你一个 m x n 的矩阵 mat 和一个整数 k ,请你返回一个矩阵 answer ,其中每个 answer[i][j] 是所有满足下述条件的元素 mat[r][c] 的和: · i - k <= r <= i + k, · j - k <= c <= j + k 且 · (r, c) 在矩阵内。
解题方法
- 动态规划(记忆化搜索||二维前缀和)
解题思路:
- 动态规划:我们算的res矩阵实质上是在求原矩阵各种的区域和,如果我们能把每个前缀的和记录下来,那么在计算res矩阵的时候,就可以靠这个矩阵(后面称为dp矩阵)来记忆化搜索,可以节省大量时间(如果直接计算区域和,则每次需要算k*k次),具体如图示

实现代码
- 本题使用java实现
class Solution {
public int[][] matrixBlockSum(int[][] mat, int k) {
int[][] res = new int[mat.length][mat[0].length];
int[][] dp = new int[mat.length][mat[0].length];
for (int i = 0; i < dp.length; ++i) {
for(int j = 0;j<dp[0].length;++j){
dp[i][j] = (j>=1?dp[i][j-1]:0) + mat[i][j];
}
for(int j = 0;j<dp[0].length;++j){
dp[i][j] += (i>=1?dp[i-1][j]:0);
}
}
for(int i = 0;i<res.length;++i){
for(int j = 0;j<res[0].length;++j){
int temp1 = (i+k>= res.length?res.length-1:i+k);
int temp2 = (j+k>= res[0].length?res[0].length-1:j+k);
int temp3 = i-k-1;
int temp4 = j-k-1;
res[i][j] = dp[temp1][temp2] - (temp3<0?0:dp[temp3][temp2])
- (temp4<0?0:dp[temp1][temp4]) + (temp3<0||temp4<0?0:dp[temp3][temp4]);
}
}
return res;
}
}
通过截图
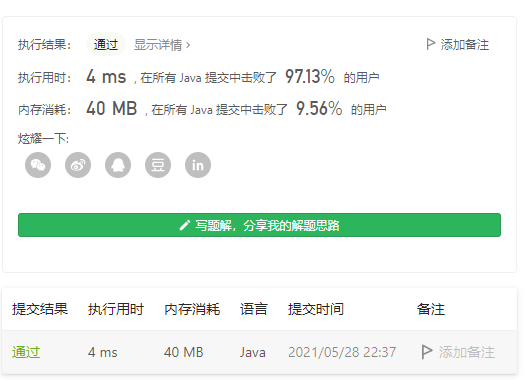
date:20210616
No:5
title:最长回文子串
description:给你一个字符串 s,找到 s 中最长的回文子串
解题方法
- 动态规划(记忆化搜索)
解题思路
- 动态规划:将字符串的每个字字符串是否为回文串记录下来,这样搜索的时候复杂度就是O(1),而暴力搜索最耗费时间的就是判断字符串是否为回文串(普通方法就是遍历所有可能,然后每一个字符串都通过一次判断方法,这样花销太大)
实现代码
- 本题使用java语言实现
class Solution {
public String longestPalindrome(String s) {
if(s.length()==1||s.length()==0)return s;
boolean[][] dp = new boolean[s.length()][s.length()];
//2到8是否为回文串,charAt(2) == charAt(8) && dp[3][7]
//1到3是否为回文串,charAt(1)==charAt(3)&& dp[2][2]
for(int i = 0;i<s.length();++i){
dp[i][0] = true;
}
Arrays.fill(dp[s.length()-1],true);
for(int i = s.length()-2;i>=0;--i){
for(int j = 1;j<s.length();++j){
dp[i][j] = i>=j?true:((s.charAt(i) == s.charAt(j)) && dp[i+1][j-1]);
//填充dp数组,将字符串的状态保存
}
}
//for(int i = 0;i<dp.length;++i){
//for(int j = 0;j<dp.length;++j){
//System.out.print(dp[i][j]);
//}
//System.out.println();
//}
int res_i = -1;//表示最长回文序列的起始坐标
int res_j = -1;//表示最长回文序列的末尾坐标
int sum = 0;//表示最长回文序列的长度
for(int i = 0;i<s.length();++i){
for(int j = s.length()-1;j> i ;--j){
int temp = j-i;
if(dp[i][j]&&temp>sum){
res_i = i;
res_j = j;
sum = temp;
//System.out.println(res_i);
//System.out.println(res_j);
//System.out.println(sum);
}
}
}
if(res_j==-1)return s.charAt(0)+"";
return s.substring(res_i,res_j+1);
}
}
通过截图

date:20210927
No:62
title:不同路径
description:一个机器人位于一个 m x n 网格的左上角 (起始点在下图中标记为 “Start” )。 机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角(在下图中标记为 “Finish” )。 问总共有多少条不同的路径?
解题方法
- 动态规划
解题思路
- 动态规划:每个位置最终的路径条数和它左边和上边儿的路径数有关,动态规划方程为dp[i][j] = dp[i-1][j] + dp[i][j-1],i代表行数,j代表列数(棋盘坐标)
- 优化:可以用滚动数组优化,由于每一次的最终结果只和上一行和前一个有关,所以只需定义一个一维数组,来记录上一行信息就行,在更新下一行时,覆盖当前行就行(由于不需要记录所有的路径,只需要最终结果,所以可以优化空间)
实现代码
- 本题使用java语言实现
//未优化代码
class Solution {
public int uniquePaths(int m, int n) {
int[][] dp = new int[m][n];
//initialize
for (int i = 0; i < dp[0].length; i++) {
dp[0][i] = 1;
}
for (int i = 0; i < dp.length; i++) {
dp[i][0] = 1;
}
for (int i = 1; i < dp.length; i++) {
for (int i1 = 1; i1 < dp[i].length; i1++) {
dp[i][i1] = (dp[i-1][i1]) + (dp[i][i1-1]);
}
}
return dp[dp.length-1][dp[0].length-1];
}
}
//优化后代码
class Solution {
public int uniquePaths(int m, int n) {
int[] dp = new int[n];
//initialize
for (int i = 0; i < dp.length; i++) {
dp[i] = 1;
}
for (int i = 1; i < m; i++) {
for (int i1 = 1; i1 < n; i1++) {
dp[i1] = dp[i1] + dp[i1-1];
}
}
return dp[n-1];
}
}
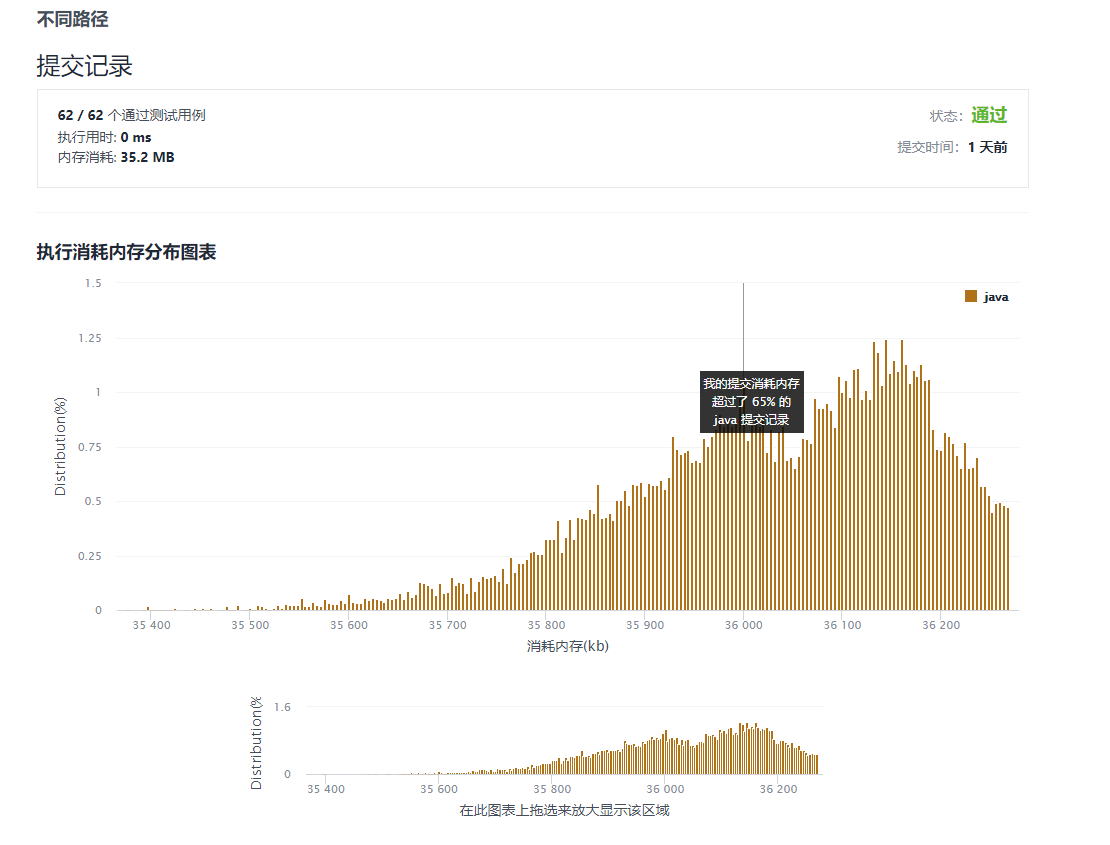
通过截图
-
优化前
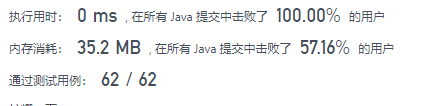
-
优化后
date:20210927
No:63
title:不同路径II
description:一个机器人位于一个 m x n 网格的左上角 (起始点在下图中标记为“Start” )。 机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角(在下图中标记为“Finish”)。 现在考虑网格中有障碍物。那么从左上角到右下角将会有多少条不同的路径?
解题方法
- 动态规划
解题思路
- 动态规划:每个位置最终的路径条数和它左边和上边儿的路径数有关,如果有障碍,则取值0即可(障碍没有到达路径),动态规划方程为dp[i][j] = dp[i-1][j] + dp[i][j-1],i代表行数,j代表列数(棋盘坐标)
- 优化:可以用滚动数组优化,由于每一次的最终结果只和上一行和前一个有关,所以只需定义一个一维数组,来记录上一行信息就行,在更新下一行时,覆盖当前行就行(由于不需要记录所有的路径,只需要最终结果,所以可以优化空间)
实现代码
- 本题使用java语言实现
//优化前
class Solution {
public int uniquePathsWithObstacles(int[][] obstacleGrid) {
if(obstacleGrid[0][0]==1) return 0;
int[][] dp = new int[obstacleGrid.length][obstacleGrid[0].length];
for (int i = 0; i < obstacleGrid.length; i++) {
for (int i1 = 0; i1 < obstacleGrid[i].length; i1++) {
if (obstacleGrid[i][i1]==1){
dp[i][i1] = -1;//pick the obstacle
}
}
}
//initialize
for (int i = 0; i < dp[0].length; i++) {
if(dp[0][i]!=-1)
dp[0][i] = 1;
else break;
}
for (int i = 0; i < dp.length; i++) {
if(dp[i][0]!=-1)
dp[i][0] = 1;
else break;
}
for (int i = 1; i < dp.length; i++) {
for (int i1 = 1; i1 < dp[i].length; i1++) {
if(dp[i][i1]!=-1){
//if it's not the obstacle,value it for the sum of the left one and upper one
// System.out.println(dp[i-1][i1]==-1?0:dp[i-1][i1]);
// System.out.println(dp[i][i1-1]==-1?0:dp[i][i1-1]);
dp[i][i1] = (dp[i-1][i1]==-1?0:dp[i-1][i1]) + (dp[i][i1-1]==-1?0:dp[i][i1-1]);
}
}
}
return dp[dp.length-1][dp[0].length-1]==-1?0:dp[dp.length-1][dp[0].length-1];
}
}
//优化后
class Solution {
public int uniquePathsWithObstacles(int[][] obstacleGrid) {
int n = obstacleGrid.length, m = obstacleGrid[0].length;
int[] f = new int[m];
f[0] = obstacleGrid[0][0] == 0 ? 1 : 0;
for (int i = 0; i < n; ++i) {
for (int j = 0; j < m; ++j) {
if (obstacleGrid[i][j] == 1) {
f[j] = 0;
continue;
}
if (j - 1 >= 0 && obstacleGrid[i][j - 1] == 0) {
f[j] += f[j - 1];
}
}
}
return f[m - 1];
}
}
通过截图
-
优化前

-
优化后
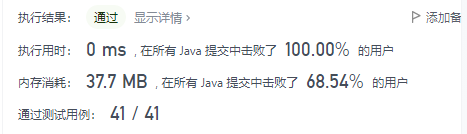
date:20210927
No:97
title:交错字符串
description:给定三个字符串 s1、s2、s3,请你帮忙验证 s3 是否是由 s1 和 s2 交错 组成的。 两个字符串 s 和 t 交错 的定义与过程如下,其中每个字符串都会被分割成若干 非空 子字符串: s = s1 + s2 + ... + sn t = t1 + t2 + ... + tm |n - m| <= 1 交错 是 s1 + t1 + s2 + t2 + s3 + t3 + ... 或者 t1 + s1 + t2 + s2 + t3 + s3 + ... 提示:a + b 意味着字符串 a 和 b 连接。
解题方法
- 动态规划
解题思路
- 动态规划:
- 思路:如果s3的长度不等于之前两个字符串长度之和,那肯定就返回False;如果等于,那如果s1的第i个字符等于s3的第i+j个字符,则s3的前i+j的部分能否由s1的前i部分和s2的前j部分组成取决于s3的前i+j-1部分能否由s1的前i-1部分和s2的前j部分组成。所以动态方程就出来了(动态规划类问题只要把父问题和子问题的关系搞清楚了,就好做了)
- f(i,j) = [f(i-1,j) & s1[i] == s3[i+j]] | [f(i,j-1) & s2[j] == s3[i+j]](此处和代码中有出入,因为字符串下表从0开始,方程是从1开始,所以代码中需要减一)
- 优化:可以用滚动数组优化,由于每一次的最终结果只和上一行和前一个有关,所以只需定义一个一维数组,来记录上一行信息就行,在更新下一行时,覆盖当前行就行(由于不需要记录所有的路径,只需要最终结果,所以可以优化空间)
实现代码
- 本题使用java语言实现
//优化前
public static boolean isInterleave(String s1, String s2, String s3) {
/*
* 思路:如果s3的长度不等于之前两个字符串长度之和,那肯定就返回False
* 如果等于,那如果s1的第i个字符等于s3的第i+j个字符,则s3的前i+j的部分能否由s1的前i部分和s2的前j部分组成取决于s3的前i+j-1部分能否由s1的前i-1部分和s2的前j部分组成
* 所以动态方程就出来了(动态规划类问题只要把父问题和子问题的关系搞清楚了,就好做了)
* f(i,j) = [f(i-1,j) & s1[i] == s3[i+j]] | [f(i,j-1) & s2[j] == s3[i+j]]
*/
int s1_len = s1.length();
int s2_len = s2.length();
int s3_len = s3.length();
if(s1_len+s2_len!=s3_len) return false;//如果不等不用进行下一步
boolean[][] dp = new boolean[s1_len+1][s2_len+1];
dp[0][0] = true;//初始化,开始位置为true,也就是说s1的第0个位置和s2的第0个位置已经可以组成s3的0+0个位置
for (int i = 0; i < s1_len+1; i++) {
for (int j = 0; j < s2_len+1; j++) {
int p = i + j - 1;
if(i>0) {
dp[i][j] = dp[i][j] || (dp[i-1][j] && (s1.charAt(i-1)==s3.charAt(p)));
}
if(j>0){
dp[i][j] = dp[i][j] || (dp[i][j-1] && (s2.charAt(j-1)==s3.charAt(p)));
}
}
}
return dp[s1_len][s2_len];
}
//优化后
class Solution {
public boolean isInterleave(String s1, String s2, String s3) {
int s1_len = s1.length();
int s2_len = s2.length();
int s3_len = s3.length();
if(s1_len+s2_len!=s3_len) return false;//如果不等不用进行下一步
boolean[] dp = new boolean[s2_len+1];
dp[0] = true;//初始化,开始位置为true,也就是说s1的第0个位置和s2的第0个位置已经可以组成s3的0+0个位置
for (int i = 0; i < s1_len+1; i++) {
for (int j = 0; j < s2_len+1; j++) {
int p = i + j - 1;
if(i>0) {
dp[j] = dp[j] && (s1.charAt(i-1)==s3.charAt(p));
}
if(j>0){
dp[j] = dp[j] || (dp[j-1] && (s2.charAt(j-1)==s3.charAt(p)));
}
}
}
return dp[s2_len];
}
}
通过截图
-
优化前
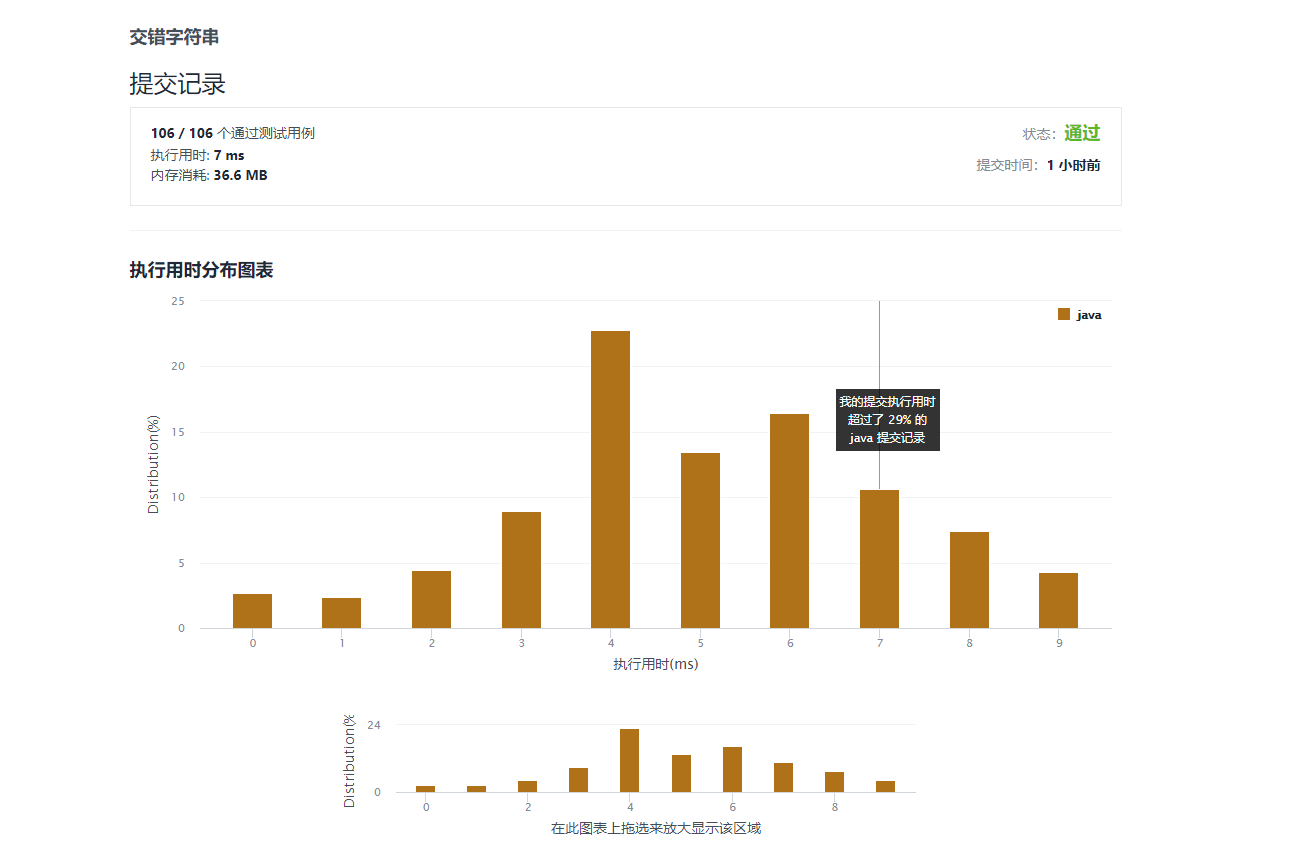
-
优化后

date:20210928
No:94
title:最小路径和
description:给定一个包含非负整数的 m x n 网格 grid ,请找出一条从左上角到右下角的路径,使得路径上的数字总和为最小。 说明:每次只能向下或者向右移动一步。
解题方法
- 动态规划
解题思路
- 动态规划:
- 思路:从左上角到每一个格子的最小值和它左边儿和上边儿的格子的最短路径有关,所以动态规划方程就出来了
- dp[i][j] = Math.min(dp[i-1][j]+grid[i][j],dp[i][j-1]+grid[i][j])//判断最短路径是哪一个
- 根据滚动数组优化:
- dp[j] = Math.min(dp[j]+grid[i][j],dp[j-1]+grid[i][j])
实现代码
- 本题使用java语言实现
package algorithm;
public class MinPathSum {
public int minPathSum(int[][] grid) {
/*
* 思路:从左上角到每一个格子的最小值和它左边儿和上边儿的格子的最短路径有关,所以动态规划方程就出来了
* dp[i][j] = Math.min(dp[i-1][j]+grid[i][j],dp[i][j-1]+grid[i][j])//判断最短路径是哪一个
* 根据滚动数组优化:
* dp[j] = Math.min(dp[j]+grid[i][j],dp[j-1]+grid[i][j])
*/
int[] dp = new int[grid[0].length];
dp[0] = grid[0][0];
for (int i = 1; i < grid[0].length; i++) {
dp[i] = dp[i-1] + grid[0][i];
}
for (int i = 1; i < grid.length; i++) {
for (int j = 0; j < grid[i].length; j++) {
if(j>0)
dp[j] = Math.min(dp[j]+grid[i][j],dp[j-1]+grid[i][j]);
else
dp[j] = dp[j]+grid[i][j];
}
}
return dp[dp.length-1];
}
}
}
通过截图
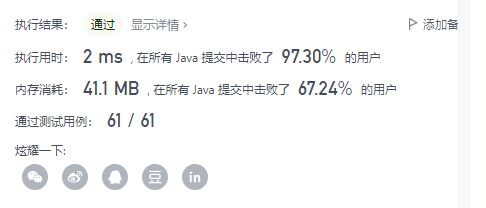
date:20210929
No:221
title:最大正方形
description:在一个由 '0' 和 '1' 组成的二维矩阵内,找到只包含 '1' 的最大正方形,并返回其面积。
解题方法
- 动态规划
- 暴力法(此处不赘述)
解题思路
- 动态规划:
- 思路:我们设定dp[i][j]为以i,j点为右下角的最大正方形的边长,就可以发现规律————这个值和它左边、上边、左上的值有关,是三个值中最小的那一个加一,所以动态规划方程就出来了
- dp[i][j] = min(dp[i-1][j],dp[i][j-1],dp[i-1][j-1])//需自定义min函数
- 根据滚动数组优化:
- dp[j] = Math.min(temp,dp[j-1],dp[j])//temp代表左上角的那个数字,由于每次数组会更新,所以左上角那个数字会更新掉,需要在更新dp[j-1]的时候缓存下来
实现代码
- 本题使用java语言实现
//优化前
private int min(int ... input){
int min = Integer.MAX_VALUE;
for (int i : input) {
min = Math.min(i,min);
}
return min;
}
public int maximalSquare(char[][] matrix) {
int[][] temp = new int[matrix.length][matrix[0].length];
for (int i = 0; i < matrix.length; i++) {
for (int i1 = 0; i1 < matrix[i].length; i1++) {
temp[i][i1] = (int) matrix[i][i1]-48;//转化
}
}
int[][] dp = new int[matrix.length][matrix[0].length];
dp[0] = temp[0];
for (int i = 0; i < temp.length; i++) {
dp[i][0] = temp[i][0];//初始化
}
for (int i = 1; i < dp.length; i++) {
for (int j = 1; j < dp[i].length; j++) {
if(temp[i][j]!=0)
dp[i][j] = min(dp[i-1][j-1],dp[i][j-1],dp[i-1][j])+1;
else
dp[i][j] = 0;
}
}
int max = -1;
for (int[] ints : dp) {
for (int anInt : ints) {
max = Math.max(max,anInt);
}
}
return (int)Math.pow(max,2);
}
//优化后,虽说使用了滚动数组优化,但是实际上提交之后的空间使用率却比优化前的高,估计是数据规模不够大导致的,小数据量直接用二维数组增加不了多少开销
class Solution {
private int min(int ... input){
int min = Integer.MAX_VALUE;
for (int i : input) {
min = Math.min(i,min);
}
return min;
}
public int maximalSquare(char[][] matrix) {
int[][] temp = new int[matrix.length][matrix[0].length];
int max = -1;
for (int i = 0; i < matrix.length; i++) {
for (int i1 = 0; i1 < matrix[i].length; i1++) {
temp[i][i1] = (int) matrix[i][i1]-48;//转化
if(temp[i][i1]==1)max = 1;
}
}
int[] dp = temp[0];
for (int i = 1; i < matrix.length; i++) {
int ss = dp[0];
dp[0] = temp[i][0];
for (int j = 1; j < matrix[i].length; j++) {
if(temp[i][j]!=0) {
int b = min(ss, dp[j - 1], dp[j]) + 1;
ss = dp[j];
dp[j] = b;
if(dp[j]>max) max = dp[j];
}else
dp[j] = 0;
}
}
return max==-1?0:(int)Math.pow(max,2);
}
}
通过截图
-
优化前

-
优化后

date:20210930
No:115
title:掷骰子的N种方法
description:这里有 d 个一样的骰子,每个骰子上都有 f 个面,分别标号为 1, 2, ..., f。 我们约定:掷骰子的得到总点数为各骰子面朝上的数字的总和。 如果需要掷出的总点数为 target,请你计算出有多少种不同的组合情况(所有的组合情况总共有 f^d 种),模 10^9 + 7 后返回。
解题方法
- 动态规划
解题思路
- 动态规划:
- 思路:设dp[i][j]表示扔i个骰子,和为j的组合个数,那么如果设第i次投骰子的值为k,则i-1次投骰子的和为j-k,又因为k非一个固定值(骰子有多少个面,它就有多少个值,都可以取到),则dp[i]和dp[i-1]的关系有
- dp[i][j] = dp[i-1][j-1]+dp[i-1][j-2]+……+dp[i-1]j-k
- 备注:代码中的1000000007一定不要用109+7代替,java中代表的是异或运算,如果不想写那么多,可以写1e9+7
实现代码
- 本题使用java语言实现
class Solution {
public int numRollsToTarget(int d, int f, int target) {
if(d*f<target||d>target) return 0;//如果目标大于所有最大值之和,直接返回0
/*
* 思路:设dp[i][j]表示扔i个骰子,和为j的组合个数,那么如果设第i次投骰子的值为k,则i-1次投骰子的和为j-k
* 又因为k非一个固定值(骰子有多少个面,它就有多少个值,都可以取到)
* 则dp[i]和dp[i-1]的关系有
* dp[i][j] = dp[i-1][j-1]+dp[i-1][j-2]+……+dp[i-1][j-k](对应骰子的不同取值)
*/
int[][] dp = new int[d+2][target+1];
int min = Math.min(f, target);
for (int i = 1; i <= min; i++) {
dp[1][i] = 1;
}
for (int i = 2; i <= d; i++) {
for(int j = 1;j <= target;++j){
for(int k = 1;k<=f && k<=j;++k){
dp[i][j] = (dp[i][j] + dp[i - 1][j - k]) % 1000000007;
}
}
}
return dp[d][target];
}
}
通过截图
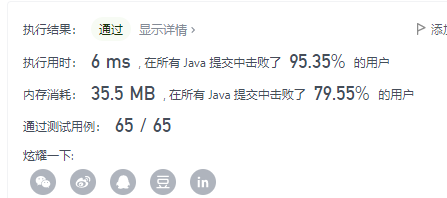
date:20211004
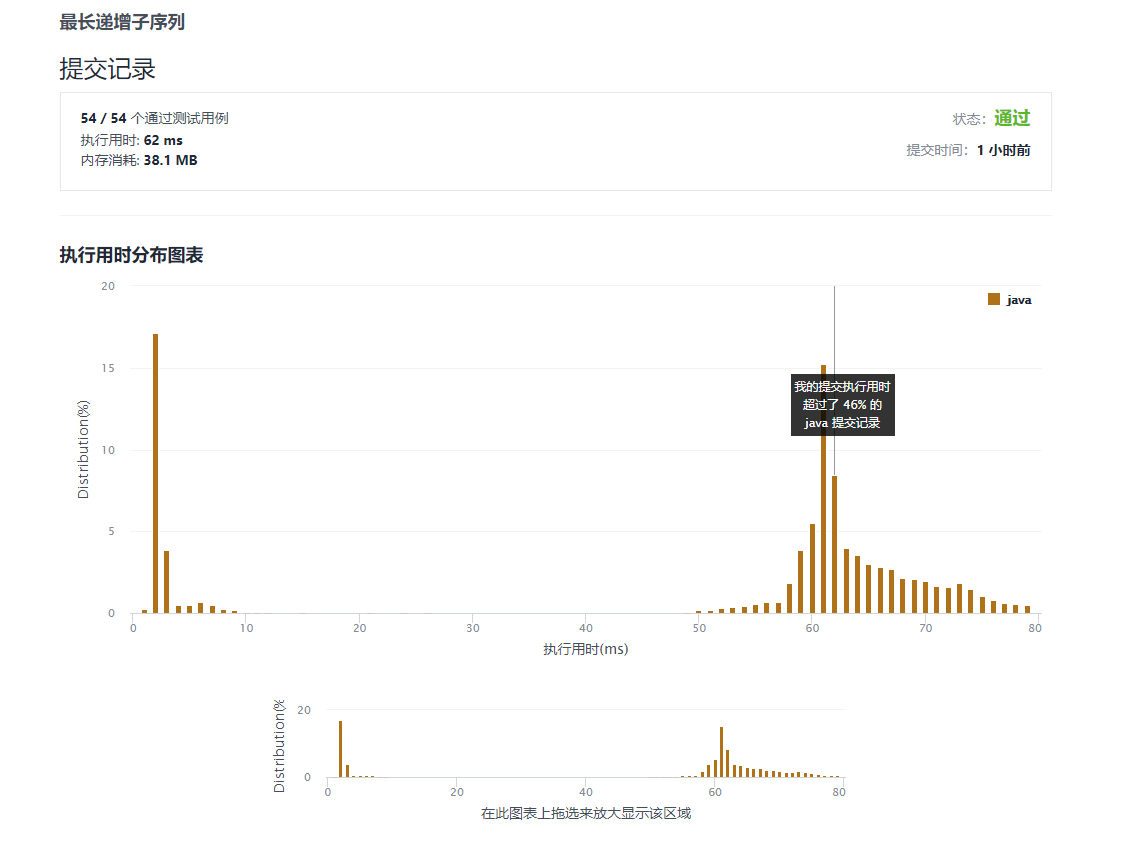
No:300
title:最长递增子序列
description:给你一个整数数组 nums ,找到其中最长严格递增子序列的长度。 子序列是由数组派生而来的序列,删除(或不删除)数组中的元素而不改变其余元素的顺序。例如,[3,6,2,7] 是数组 [0,3,1,6,2,2,7] 的子序列。
解题方法
- 动态规划
解题思路
- 动态规划:
- 思路:设dp[i]为以第i个数字为结尾的最长增长子序列的长度,则根据递推关系,dp[i]根据此前记录的dp[0]-dp[i-1]以及nums[i]更新,讲的不是很清楚,具体看代码,大致就是一轮又一轮的遍历,来不断更新dp
实现代码
- 本题使用java语言实现
public int lengthOfLIS(int[] nums) {
/*
* 思路:设dp[i]为以第i个数字为结尾的最长增长子序列的长度
* 则根据递推关系,dp[i]根据此前记录的dp[0]-dp[i-1]以及nums[i]更新
* 讲的不是很清楚,具体看代码
* 大致就是一轮又一轮的遍历,来不断更新dp
*/
int[] dp = new int[nums.length];
dp[0] = 1;//如果以第一个数字作为结尾,则它的最长增长子序列就是他自己,长度为1
int max = 0;
for(int i = 1;i<nums.length;++i){
for(int j = 0;j<i;++j){
if(nums[i]>nums[j])
dp[i] = Math.max(dp[i],dp[j]+1);//更新dp值
}
max = Math.max(max,dp[i]);//记录dp数组中的最大值
}
return max;
}
通过截图
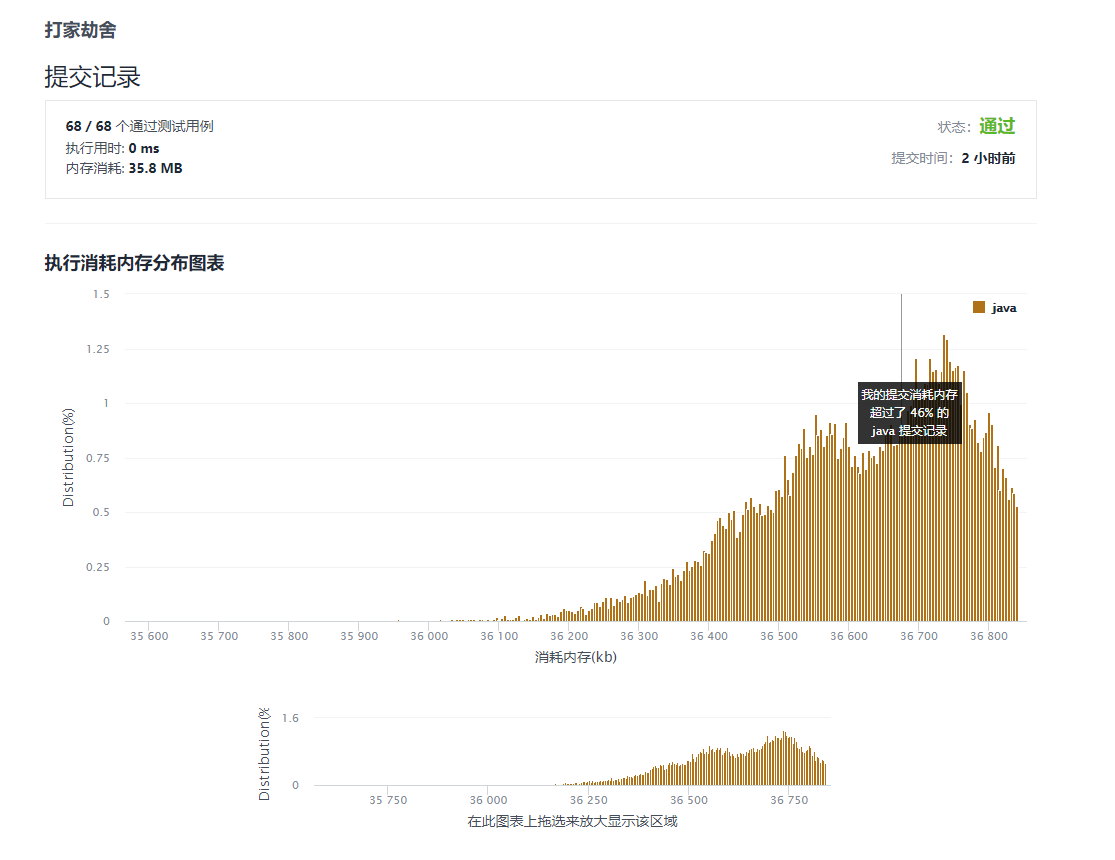
date:20211005
No:198
title:打家劫舍
description:你是一个专业的小偷,计划偷窃沿街的房屋。每间房内都藏有一定的现金,影响你偷窃的唯一制约因素就是相邻的房屋装有相互连通的防盗系统,如果两间相邻的房屋在同一晚上被小偷闯入,系统会自动报警。 给定一个代表每个房屋存放金额的非负整数数组,计算你 不触动警报装置的情况下 ,一夜之内能够偷窃到的最高金额。
解题方法
- 动态规划
解题思路
- 动态规划:
- 思路:原版————>设dp[i]为到当前位置位置能偷到最多的钱(当前位置必偷),则dp[i] = Math.max(dp[i-2],dp[i-3]) + nums[i],因为如果当前位置必偷,则前一个位置肯定不能偷,那么如果只继承往前第二个位置,就会漏掉很多情况,所以需要做一个比较,和前第三个位置进行比较,这样不会有漏掉的情况
- 思路:官方版本————>当前位置不是必偷,而是如果当前位置加上前第二个位置的和没有前一个位置多,那么直接继承前一个位置,dp[i] = Math.max(dp[i-1],dp[i-2]+nums[i])
实现代码
- 优化:可使用滚动数组优化,将一维数组压缩到常数级
- 本题使用java语言实现
//原始版本(未优化)
public int rob(int[] nums) {
/*
* 思路:原版————>设dp[i]为到当前位置位置能偷到最多的钱(当前位置必偷),则dp[i] = Math.max(dp[i-2],dp[i-3]) + nums[i]
* 因为如果当前位置必偷,则前一个位置肯定不能偷,那么如果只继承往前第二个位置,就会漏掉很多情况
* 所以需要做一个比较,和前第三个位置进行比较,这样不会有漏掉的情况
*/
if(nums.length==1) return nums[0];
int[] dp = new int[nums.length];
dp[0] = nums[0];
dp[1] = nums[1];
for (int i = 2; i < dp.length; i++) {
if(i==2)
dp[i] =nums[i]+dp[i-2];
else
dp[i] = Math.max(dp[i-2],dp[i-3])+nums[i];
}
return Math.max(dp[nums.length-1],dp[nums.length-2]);
}
//官方版本(未优化)
public int rob01(int[] nums) {
/*
* 思路:改进版:当前位置不是必偷,而是如果当前位置加上前第二个位置的和没有前一个位置多,那么直接继承前一个位置
* dp[i] = Math.max(dp[i-1],dp[i-2]+nums[i])
*/
if(nums.length==1) return nums[0];
int[] dp = new int[nums.length];
dp[0] = nums[0];
dp[1] = Math.max(nums[1],nums[0]);//这里也要使用dp策略
for (int i = 2; i < dp.length; i++) {
dp[i] = Math.max(dp[i-2]+nums[i],dp[i-1]);
}
return dp[nums.length-1];
}
//原始版本(已优化)
public int rob02(int[] nums) {
/*
* 思路:原版的优化版本:使用滚动数组优化
*/
if(nums.length==1) return nums[0];
int temp1 = nums[0];
int temp2 = nums[1];
int last = 0;
for (int i = 2; i < nums.length; i++) {
int temp =temp1;
if(i==2) {
temp1 = temp2;
temp2 = nums[i] + temp;
}else {
temp1 = temp2;
temp2 = Math.max(temp, last) + nums[i];
}
last = temp;
}
return Math.max(temp1,temp2);
}
//官方版本(已优化)
public int rob03(int[] nums) {
/*
* 思路:改进版的优化版本:使用滚动数组优化
*/
if(nums.length==1) return nums[0];
int temp1 = nums[0];
int temp2 = Math.max(nums[1],nums[0]);//这里也要使用dp策略
for (int i = 2; i < nums.length; i++) {
int temp = temp1+nums[i];
temp1 = temp2;
temp2 = Math.max(temp,temp2);
}
return temp2;
}
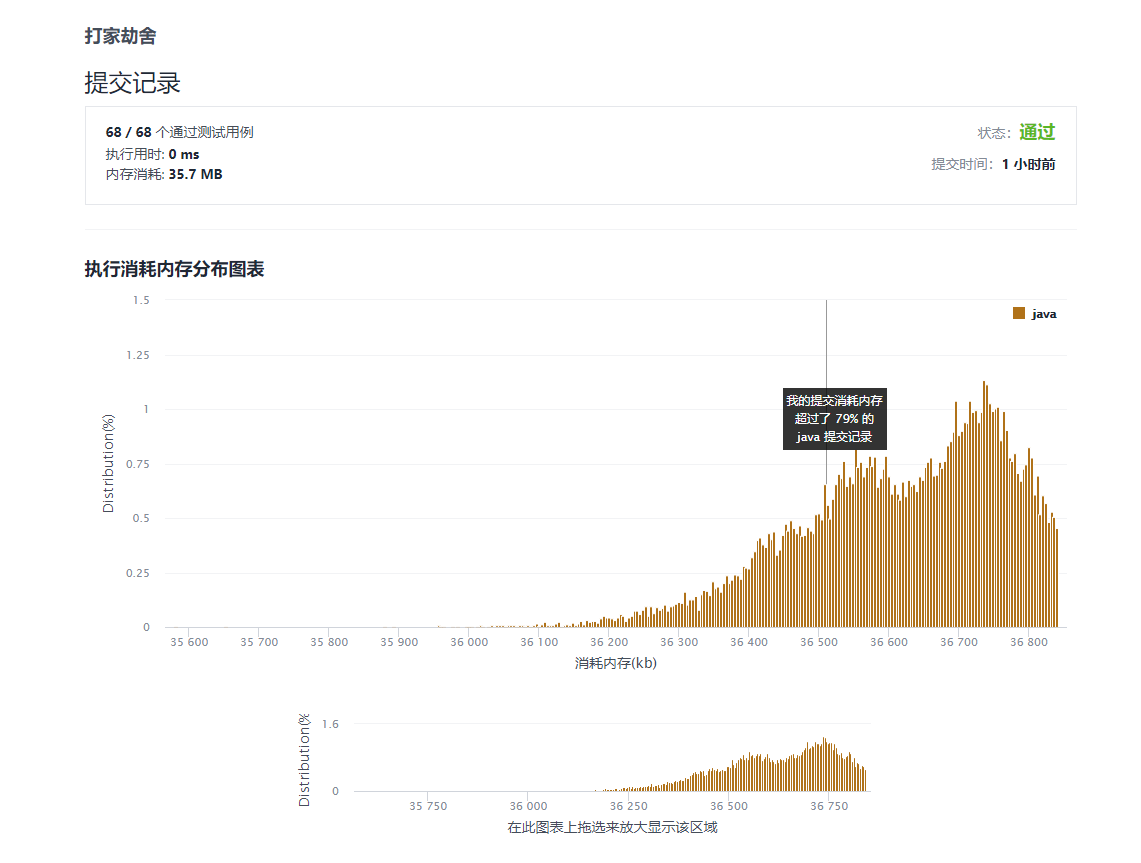
通过截图
-
原始版本未优化
-
官方版本未优化

-
原始版本优化

-
官方版本优化
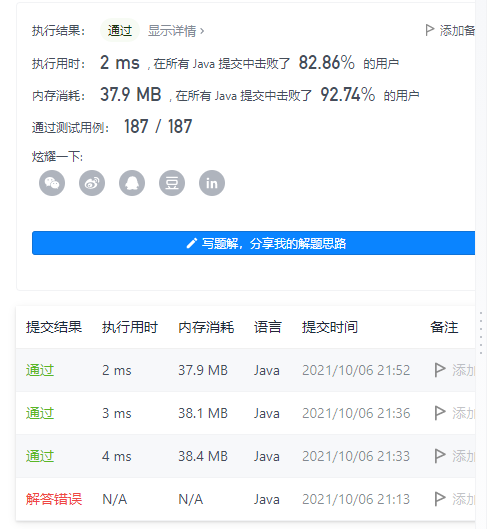
date:20211006
No:152
title:乘积最大子数组
description:给你一个整数数组 nums ,请你找出数组中乘积最大的连续子数组(该子数组中至少包含一个数字),并返回该子数组所对应的乘积。
解题方法
- 动态规划
解题思路
- 动态规划:
- 思路:设lastOne_p为以当前位置为结尾最大连续子序列的乘积的值,lastOne_n为以当前位置为结尾的最小连续子序列的乘积的值(如果有负负得正的情况,最小值就用的到,因为数值允许有负数)
实现代码
- 优化:可使用滚动数组优化,将一维数组压缩到常数级(所有dp如果无需记录所有的阶段,都可以使用滚动数组优化,至少可以压缩一维)
- 本题使用java语言实现
class Solution {
private int[] getExe(int ... inputs){
int max = Integer.MIN_VALUE;
int min = Integer.MAX_VALUE;
for (int input : inputs) {
max = Math.max(input,max);
min = Math.min(input,min);
}
int[] res = new int[2];
res[0] = max;
res[1] = min;
return res;
}
public int maxProduct(int[] nums) {
int lastOne_p = nums[0];
int lastOne_n = nums[0];
int max = nums[0];
for (int i = 1; i < nums.length; i++) {
int[] res_temp = getExe(nums[i],lastOne_p*nums[i],lastOne_n*nums[i]);
lastOne_p = res_temp[0];
lastOne_n = res_temp[1];
max = Math.max(lastOne_p,max);
}
return max;
}
}
通过截图
- 前几次通过是未优化的,第一次到第二次优化了获取极值的算法,每次循环压缩了一次运算的时间,第二次到第三次优化了dp数组,将一维数组压缩到常量级
date:20211009
No:213
title:打家劫舍II
description:你是一个专业的小偷,计划偷窃沿街的房屋,每间房内都藏有一定的现金。这个地方所有的房屋都 围成一圈 ,这意味着第一个房屋和最后一个房屋是紧挨着的。同时,相邻的房屋装有相互连通的防盗系统,如果两间相邻的房屋在同一晚上被小偷闯入,系统会自动报> > 警 。 给定一个代表每个房屋存放金额的非负整数数组,计算你 在不触动警报装置的情况下 ,今晚能够偷窃到的最高金额。
解题方法
- 动态规划
解题思路
- 动态规划:
- 思路:当前位置不是必偷,而是如果当前位置加上前第二个位置的和没有前一个位置多,那么直接继承前一个位置,dp[i] = Math.max(dp[i-1],dp[i-2]+nums[i]),但是因为房屋是一个圈没所以要分两种情况,第一种情况是第一家偷,那么最后一家就不能偷,第二种情况是第二家偷,那么最后一家就可以偷,设置好循环的边界,就A了
实现代码
- 优化:可使用滚动数组优化,将一维数组压缩到常数级
- 本题使用java语言实现
//优化前
class Solution {
public int rob(int[] nums) {
if(nums.length==1) return nums[0];
int[] dp01 = new int[nums.length];
int[] dp02 = new int[nums.length];
dp01[0] = nums[0];//第一家偷
dp02[1] = nums[1];//第一家不偷
int max01 = dp01[0];
int max02 = dp02[1];
for (int i = 1; i < nums.length-1; i++) {
if (i == 1) {
dp01[i] = Math.max(dp01[i-1],nums[i]);
max01 = dp01[i];
} else {
dp01[i] = Math.max(dp01[i - 2] + nums[i], dp01[i - 1]);
max01 = Math.max(max01, dp01[i]);
}
}
for (int i = 2; i < nums.length; i++) {
if (i == 2) {
dp02[i] = Math.max(dp02[i-1],nums[i]);
max02 = dp02[i];
} else {
dp02[i] = Math.max(dp02[i - 2] + nums[i], dp02[i - 1]);
max02 = Math.max(max02, dp02[i]);
}
}
return Math.max(max01,max02);
}
}
//优化后
public int rob(int[] nums) {
if(nums.length==1) return nums[0];
int dp01_cur = nums[0];
int dp01_last = nums[0];
int dp02_cur = nums[1];
int dp02_last = nums[1];
int max01 = dp01_cur;
int max02 = dp02_cur;
for (int i = 1; i < nums.length-1; i++) {
int temp = dp01_cur;
if (i == 1) {
dp01_cur = Math.max(dp01_cur,nums[i]);
max01 = dp01_cur;
} else {
dp01_cur = Math.max(dp01_last + nums[i], dp01_cur);
max01 = Math.max(max01, dp01_cur);
}
dp01_last = temp;
}
for (int i = 2; i < nums.length; i++) {
int temp = dp02_cur;
if (i == 2) {
dp02_cur = Math.max(dp02_cur,nums[i]);
max02 = dp02_cur;
} else {
dp02_cur = Math.max(dp02_last + nums[i], dp02_cur);
max02 = Math.max(max02, dp02_cur);
}
dp02_last = temp;
}
return Math.max(max01,max02);
}
通过截图
-
未优化
-
优化后
date:20211014
No:337
title:打家劫舍III
description:在上次打劫完一条街道之后和一圈房屋后,小偷又发现了一个新的可行窃的地区。这个地区只有一个入口,我们称之为“根”。 除了“根”之外,每栋房子有且只有一个“父“房子与之相连。一番侦察之后,聪明的小偷意识到“这个地方的所有房屋的排列类似于一棵二叉?> 树”。 如果两个直接相连的房子在同一天晚上被打劫,房屋将自动报警。 计算在不触动警报的情况下,小偷一晚能够盗取的最高金额。
解题方法
- 动态规划
解题思路
- 动态规划:
- 思路:当前节点有两个选择,一个是选择当前节点,这种情况下子节点的任何一个都不能选择;第二个是不选择当前节点,则子节点可以选也可以不许选,那么我们设f(o)为选择取当前节点时能偷取得最大数额,设g(o)为不选取当前节点时能偷取得最大数额(设置两个Map存储,则f(o) = o.val+g(o.l)+g(o.r),g(o) = Math.max(f(o.l),g(o.l))+Math.max(f(o.r),g(o.r))
- 优化:可使用滚动数组优化,将一维数组压缩到常数级
实现代码
- 本题使用java语言实现
//优化前
Map<TreeNode01,Integer> f = new HashMap<>();
Map<TreeNode01,Integer> g = new HashMap<>();
public int rob(TreeNode01 root){
dfs(root);
return Math.max(f.getOrDefault(root,0),g.getOrDefault(root,0));
}
private void dfs(TreeNode01 root){
if(root == null){
return;
}
dfs(root.left);
dfs(root.right);
f.put(root,root.val+g.getOrDefault(root.left,0)+g.getOrDefault(root.right,0));
g.put(root,Math.max(f.getOrDefault(root.left,0),g.getOrDefault(root.left,0))
+Math.max(f.getOrDefault(root.right,0),g.getOrDefault(root.right,0)));
}
//优化后
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode() {}
* TreeNode(int val) { this.val = val; }
* TreeNode(int val, TreeNode left, TreeNode right) {
* this.val = val;
* this.left = left;
* this.right = right;
* }
* }
*/
class Solution {
// Map<TreeNode,Integer> f = new HashMap<>();
// Map<TreeNode,Integer> g = new HashMap<>();
public int rob(TreeNode root){
int[] result = dfs(root);
return Math.max(result[0],result[1]);
}
private int[] dfs(TreeNode root){
if(root == null){
return new int[]{0,0};
}
int[] left = dfs(root.left);
int[] right =dfs(root.right);
int[] result = {0,0};
result[0] = root.val + left[1]+right[1];
result[1] = Math.max(left[0],left[1])+Math.max(right[0],right[1]);
return result;
}
}
通过截图
-
未优化
-
优化后
date:20211020
No:122
title:买卖股票的最佳时机 II
description:给定一个数组 prices ,其中 prices[i] 是一支给定股票第 i 天的价格。 设计一个算法来计算你所能获取的最大利润。你可以尽可能地完成更多的交易(多次买卖一支股票)。 注意:你不能同时参与多笔交易(你必须在再次购买前出售掉之前的股票)。
解题方法
- 动态规划
解题思路
- 动态规划:
- 思路(动态规划):在每一天,客户有两种状态,第一种是持有股票,第二种是不持有股票,那么我们在每一天设定两个值,第一个是选择持有股票的时候当前能获取的最大利润,第二个是不持有股票的时候当前能获取的最大利润,则dp[i][0] = Math.max(dp[i-1][1]-prices[i],dp[i-1][0])//当天持有股票分两种,一种是前一天不持有,则今天买,减去的是买的钱第二种是前一天持有,今天继续持有,直接继承前一天的最大利润就行,因为不卖掉,最大利润是不会变得dp[i][1] = Math.max(dp[i-1][1],dp[i-1][0]+prices[i])//当天不持有股票也分两种,一种是前一天也不持有,那今天继续不持有,则不赚也不亏第二种是前一天持有,今天不持有,也就是说卖掉了,那么加上的就是前一天持有的最大利润加上卖掉的钱
- 思路(贪心):问题可以抽象为在一个总区间寻找不重叠的子区间满足下面的公式最后的值最大,设每个区间头为r,尾为t;∑(i∈(1,n))ti-ri,则该公式可以变换为在每一次天数变换时如果后一天价格比前一天高,那就加上;==>res += Math.max(0,prices[i]-prices[i-1])
- 优化:可使用滚动数组优化,将一维数组压缩到常数级
实现代码
- 本题使用java语言实现
//优化后,优化前的不放了,思路已经讲清楚了
public int maxProfit01(int[] prices){
/*
* 思路:在每一天,客户有两种状态,第一种是持有股票,第二种是不持有股票,
* 那么我们在每一天设定两个值,第一个是选择持有股票的时候当前能获取的最大利润,第二个是不持有股票的时候当前能获取的最大利润
* 则
* dp[i][0] = Math.max(dp[i-1][1]-prices[i],dp[i-1][0])//当天持有股票分两种,一种是前一天不持有,则今天买,减去的是买的钱
* 第二种是前一天持有,今天继续持有,直接继承前一天的最大利润就行,因为不卖掉,最大利润是不会变得
* dp[i][1] = Math.max(dp[i-1][1],dp[i-1][0]+prices[i])//当天不持有股票也分两种,一种是前一天也不持有,那今天继续不持有,则不赚也不亏
* 第二种是前一天持有,今天不持有,也就是说卖掉了,那么加上的就是前一天持有的最大利润加上卖掉的钱
*/
int last_in = -prices[0];
int last_unin = 0;
for (int i = 1; i < prices.length; i++) {
int temp1 = last_in;
last_in = Math.max(last_unin-prices[i],temp1);
last_unin = Math.max(last_unin,temp1+prices[i]);
}
return Math.max(last_in,last_unin);
}
//贪心
public int maxProfit02(int[] prices){
/*
* 贪心:思路:问题可以抽象为在一个总区间寻找不重叠的子区间满足下面的公式最后的值最大,设每个区间头为r,尾为t
* ∑(i∈(1,n))ti-ri
* 则该公式可以变换为在每一次天数变换时如果后一天价格比前一天高,那就加上
* ==>res += Math.max(0,prices[i]-prices[i-1])
*/
int res = 0;
for (int i = 1; i < prices.length; i++) {
res += Math.max(0,prices[i]-prices[i-1]);
}
return res;
}
通过截图
-
动态规划
-
贪心
date:20211021
No:123
title:买卖股票的最佳时机 III
description:给定一个数组,它的第 i 个元素是一支给定的股票在第 i 天的价格。 设计一个算法来计算你所能获取的最大利润。你最多可以完成 两笔 交易。 注意:你不能同时参与多笔交易(你必须在再次购买前出售掉之前的股票)。
解题方法
- 动态规划
解题思路
- 动态规划:
- 思路:思路:根据动态规划思想,先分析一个节点的状态,然后为每个状态构造状态转移方程,然后递推便是(看了题解之后总结的思路)一个节点共有五个状态
- 未进行过任何交易
- 进行过一次买入操作
- 完成过一笔交易(一次买入一次卖出)
- 再完成一笔交易的前提下再进行一次买入操作
- 完成两笔交易(两次买入两次卖出)
-未经行过任何交易的利益当然恒为0,所以不用记录,至于剩下的状态,我们依次设当前节点的最大利润为buy1、sell1、buy2、sell2;则状态转移方程如下
{ buy1 = Math.max(buy1(上一个节点记录的),-prices[i]) sell1 = Math.max(buy1(上一次的)+prices[i],sell1(上一次的)) buy2 = Math.max(sell1(上一次的)-prices[i],buy2(上一次的) sell2 = Math.max(sell2(上一次的),buy2(上一次的)+prices[i]) } - 思路:思路:根据动态规划思想,先分析一个节点的状态,然后为每个状态构造状态转移方程,然后递推便是(看了题解之后总结的思路)一个节点共有五个状态
实现代码
- 本题使用java语言实现
//未优化,懒得优化了/捂脸,反正弄来弄去都是压缩状态和用滚动数组压缩空间
package algorithm;
public class MaxProfit03 {
public int maxProfit(int[] prices) {
/*
* 思路:根据动态规划思想,先分析一个节点的状态,然后为每个状态构造状态转移方程,然后递推便是(看了题解之后总结的思路)
* 一个节点共有五个状态
* ·未进行过任何交易
* ·进行过一次买入操作
* ·完成过一笔交易(一次买入一次卖出)
* ·再完成一笔交易的前提下再进行一次买入操作
* ·完成两笔交易(两次买入两次卖出)
* 未经行过任何交易的利益当然恒为0,所以不用记录,至于剩下的状态,我们依次设当前节点的最大利润为buy1、sell1、buy2、sell2
* 则状态转移方程如下
* {
* buy1 = Math.max(buy1(上一个节点记录的),-prices[i])
* sell1 = Math.max(buy1(上一次的)+prices[i],sell1(上一次的))
* buy2 = Math.max(sell1(上一次的)-prices[i],buy2(上一次的)
* sell2 = Math.max(sell2(上一次的),buy2(上一次的)+prices[i])
* }
*/
int[][] dp = new int[prices.length][4];
dp[0][0] = -prices[0];
dp[0][2] = -prices[0];
for (int i = 1; i < prices.length; i++) {
dp[i][0] = Math.max(dp[i-1][0],-prices[i]);
dp[i][1] = Math.max(dp[i-1][1],dp[i-1][0]+prices[i]);
dp[i][2] = Math.max(dp[i-1][2],dp[i-1][1]-prices[i]);
dp[i][3] = Math.max(dp[i-1][3],dp[i-1][2]+prices[i]);
}
int len = prices.length;
return Math.max(dp[len-1][1],dp[len-1][3]);
}
}
通过截图
- 动态规划