数字图像处理-空间域处理-灰度变换-基本灰度变换函数（反转变换、对数变换、伽马变换和分段线性变换）

总结性的一篇博文，内容其实很简单，之所以写出来是为了对自己之前所学做一些总结。

参考自：《数字图像处理》--第三版--冈萨勒斯--中，以及师兄提供的参考资料，在此对师兄表示感谢。

 

空间域处理是直接对像素进行操作的方法，这是相对于频率域处理而言的。空间域处理主要分为两大类：灰度变换和空间滤波。灰度变换在图像单个像素上操作，主要以对比度和阈值处理为目的。空间滤波涉及改善性能的操作，通过像元领域来处理。

空间域处理均可由下式表达：

 

表示f(x, y)输入图像，g(x,y) 表示输出图像，T 是变换算子（数学规则）

灰度变换可以看作领域大小为1*1的空间域处理，这这种情况下上式变为灰度变换函数：

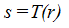
r和s分别为输入、输出灰度

基本的灰度变换函数

常用的基本函数有三类：线性函数，对数函数（对数和反对数）和幂律函数（n次幂和n次根）

图像反转

适用于增强嵌入在一幅图像暗区域中的白色或灰色细节。变换公式为：

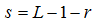
图像灰度级范围为[0，L-1]

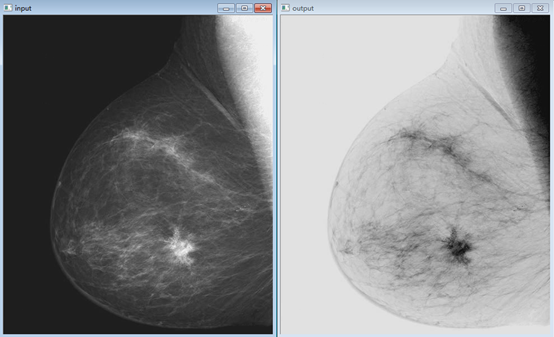
"""反转变换"""
import numpy as np
import cv2
import matplotlib.pyplot as plt


def reverse(img):
    output = 255 - img
    return output


img1 = cv2.imread(r'F:\program_study\Python\data\breast.tif')  # 前头加r是消除反斜杠转义
cv2.imshow('input', img1)
x = np.arange(0, 256, 0.01)
y = 255 - x
plt.plot(x, y, 'r', linewidth=1)
plt.title('反转变换函数图')
plt.xlim([0, 255]), plt.ylim([0, 255])
plt.show()
img_output = reverse(img1)
cv2.namedWindow('output', cv2.WINDOW_NORMAL)  # 可改变窗口大小
cv2.imshow('output', img_output)
cv2.waitKey(0)
cv2.destroyAllWindows()

对数变换

对数变换可以拉伸范围较窄的低灰度值，同时压缩范围较宽的高灰度值。可以用来扩展图像中的暗像素值，同时压缩亮像素值。

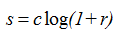
其中c为常数，r加1可以使函数向左移一个单位，得到的s均大于0。

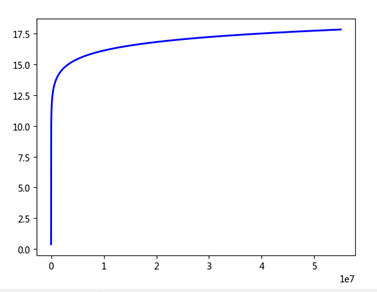
一个典型的应用是傅立叶频谱（幅度谱）的显示。对傅立叶频谱进行对数变化，左图中蓝线为变换函数，注意x轴量级为10的7次方，直接被压缩到了0-17.5，效果非常明显。右图是经过对数变换，又经过最大最小值变换后的频谱。

 

一般对数变换

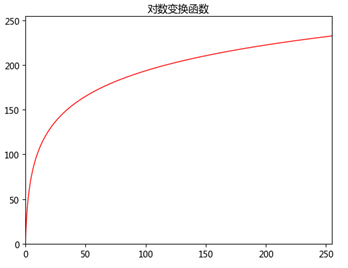
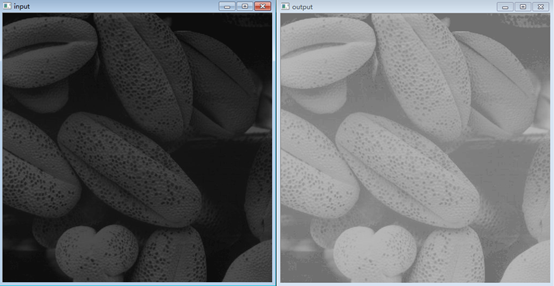
"""对数变换"""
import numpy as np
import matplotlib.pyplot as plt
import cv2


def log_plot(c):
    x = np.arange(0, 256, 0.01)
    y = c*np.log(1 + x)
    plt.plot(x, y, 'r', linewidth=1)
    plt.title('对数变换函数')
    plt.xlim(0, 255), plt.ylim(0, 255)
    plt.show()


def log(c, img):
    output_img = c*np.log(1.0+img)
    output_img = np.uint8(output_img+0.5)
    return output_img


img_input = cv2.imread('F:\program_study\Python\data\pollens.tif')
cv2.imshow('input', img_input)
log_plot(42)
img_output = log(42, img_input)
cv2.imshow('output', img_output)
cv2.waitKey(0)
cv2.destroyAllWindows()

幂律（伽马）变换

变换的基本形式为：

 

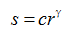
c和γ为正常数

对于不同的γ值，有不同的曲线

 

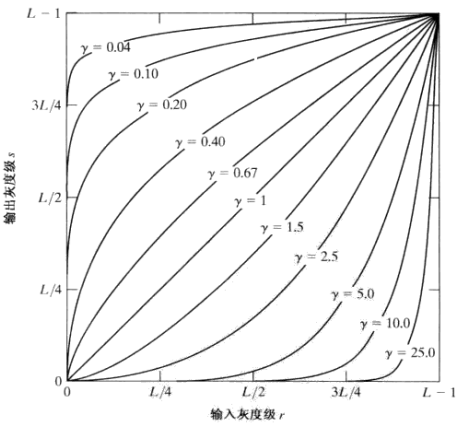
多用在图像整体偏暗，扩展灰度级。另外一种情况是，图像有“冲淡”的外观（很亮白）需要压缩中高以下的大部分的灰度级。

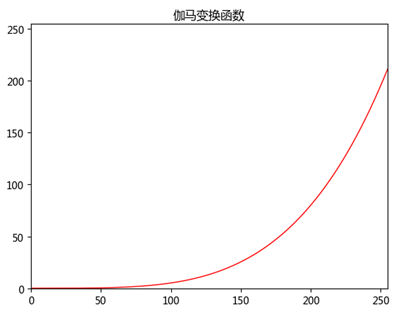
"""幂律变换（伽马）"""
import numpy as np
import matplotlib.pyplot as plt
import cv2


def gamma_plot(c, v):
    x = np.arange(0, 256, 0.01)
    y = c*x**v
    plt.plot(x, y, 'r', linewidth=1)
    plt.title('伽马变换函数')
    plt.xlim([0, 255]), plt.ylim([0, 255])
    plt.show()


def gamma(img, c, v):
    lut = np.zeros(256, dtype=np.float32)
    for i in range(256):
        lut[i] = c * i ** v
    output_img = cv2.LUT(img, lut)
    output_img = np.uint8(output_img+0.5)  # 这句一定要加上
    return output_img


img_input = cv2.imread('F:\program_study\Python\data\city.tif', cv2.IMREAD_GRAYSCALE)
cv2.imshow('imput', img_input)
gamma_plot(0.00000005, 4.0)
img_output = gamma(img_input, 0.00000005, 4.0)
cv2.imshow('output', img_output)
cv2.waitKey(0)
cv2.destroyAllWindows()

分段线性变换

　　对比度拉伸

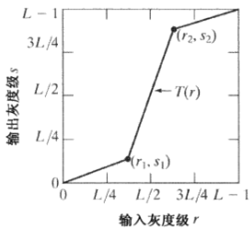
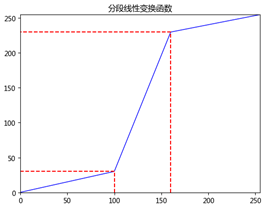
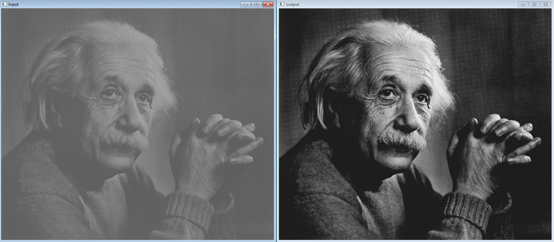
"""分段线性变换Segmental Linear Transformation"""
import cv2
import numpy as np
import matplotlib.pyplot as plt


def SLT(img, x1, x2, y1, y2):
    lut = np.zeros(256)
    for i in range(256):
            if i < x1:
                lut[i] = (y1/x1)*i
            elif i < x2:
                lut[i] = ((y2-y1)/(x2-x1))*(i-x1)+y1
            else:
                lut[i] = ((y2-255.0)/(x2-255.0))*(i-255.0)+255.0
    img_output = cv2.LUT(img, lut)
    img_output = np.uint8(img_output+0.5)
    return img_output


def SLT_plot(x1, x2, y1, y2):
    plt.plot([0, x1, x2, 255], [0, y1, y2, 255], 'b', linewidth=1)
    plt.plot([x1, x1, 0], [0, y1, y1], 'r--')
    plt.plot([x2, x2, 0], [0, y2, y2], 'r--')
    plt.title('分段线性变换函数')
    plt.xlim([0, 255]), plt.ylim([0, 255])
    plt.show()


input_img = cv2.imread('F:\program_study\Python\data\Einstein.tif', cv2.IMREAD_GRAYSCALE)
cv2.imshow('input', input_img)
img_x1 = 100
img_x2 = 160
img_y1 = 30
img_y2 = 230
SLT_plot(img_x1, img_x2, img_y1, img_y2)
output_img = SLT(input_img, img_x1, img_x2, img_y1, img_y2)
cv2.imshow('output', output_img)
cv2.waitKey(0)
cv2.destroyAllWindows()

　　灰度级分层

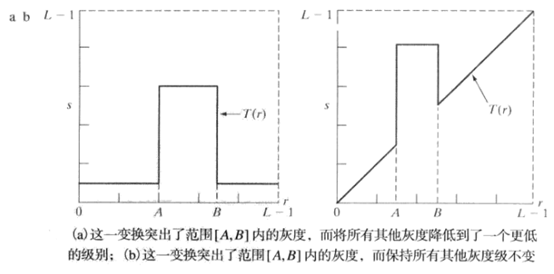
"""灰度级分层"""
import numpy as np
import cv2


def GrayLayer(img):
    lut = np.zeros(256, dtype=np.uint8)
    layer1 = 30
    layer2 = 60
    value1 = 10
    value2 = 250
    for i in range(256):
        if i >= layer2:
            lut[i] = value1
        elif i >= layer1:
            lut[i] = value2
        else:
            lut[i] = value1
    ans = cv2.LUT(img, lut)
    return ans


img_input = cv2.imread('F:\program_study\Python\data\LandsatImage.tif', cv2.IMREAD_GRAYSCALE)
cv2.imshow('input', img_input)
img_output = GrayLayer(img_input)
cv2.imshow('output', img_output)
# cv2.imwrite('LandsatImage_grayLayer.tif', img_output)
cv2.waitKey(0)
cv2.destroyAllWindows()

　　二值化

"""阈值化，其实就是二值化"""
import cv2

img_input = cv2.imread('F:\program_study\Python\data\Lena.tif', cv2.IMREAD_GRAYSCALE)
cv2.imshow('input', img_input)
threshold = 110
img_input[img_input > threshold] = 255  # 二值化
img_input[img_input <= threshold] = 0  # 二值化
cv2.imshow('output', img_input)
# cv2.imwrite('Lena_thresholding.tif', f)
cv2.waitKey(0)
cv2.destroyAllWindows()

　　最大最小值拉伸

 

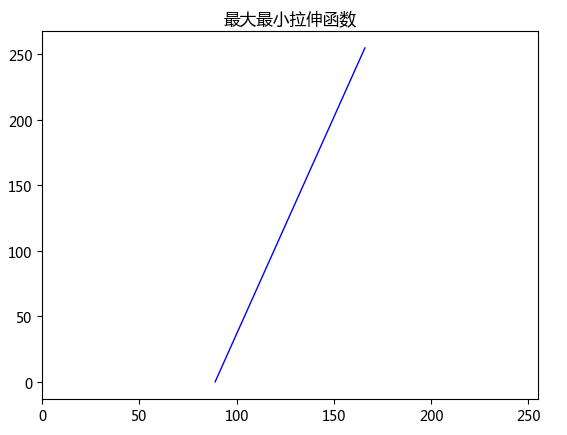
"""最大最小值拉伸"""
import numpy as np
import matplotlib.pyplot as plt
import cv2


def max_min_strech(img):
    max1 = np.max(img)
    min1 = np.min(img)
    output_img = (255.0*(img-min1))/(max1-min1)  # 注意255.0 而不是255 二者算出的结果区别很大
    output_img1 = np.uint8(output_img+0.5)
    return output_img1


img_input = cv2.imread('F:\program_study\Python\data\Einstein.tif', cv2.IMREAD_GRAYSCALE)
cv2.imshow('input', img_input)
x = (np.min(img_input), np.max(img_input))
y = (0, 255)
plt.plot(x, y, 'b', linewidth=1)
plt.title('最大最小拉伸函数')
plt.xlim(0, 255)
plt.show()
img_output = max_min_strech(img_input)
cv2.imshow('output', img_output)
cv2.waitKey(0)
cv2.destroyAllWindows()


# 最大最小值拉伸的实质是找线性函数，两点求直线方程，x1是拉伸前的最小值，
# y1是拉伸后的最小值；x2是拉伸前的最大值，y2是拉伸后的最大值