数字图像处理-频域滤波-高通/低通滤波

频域滤波

频域滤波是在频率域对图像做处理的一种方法。步骤如下：

滤波器大小和频谱大小相同，相乘即可得到新的频谱。

滤波后结果显示，低通滤波去掉了高频信息，即细节信息，留下的低频信息代表了概貌。常用的例子，比如美图秀秀的磨皮，去掉了脸部细节信息（痘坑，痘印，暗斑等）。高通滤波则相反。

高通/低通滤波

1.理想的高/低通滤波

顾名思义，高通滤波器为：让高频信息通过，过滤低频信息；低通滤波相反。

理想的低通滤波器模板为：

 

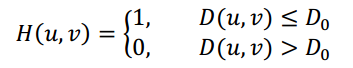
其中，D₀表示通带半径，D(u，v)是到频谱中心的距离（欧式距离），计算公式如下：

 

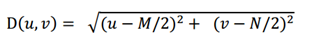
M和N表示频谱图像的大小，（M/2，N/2）即为频谱中心

理想的高通滤波器与此相反，1减去低通滤波模板即可。

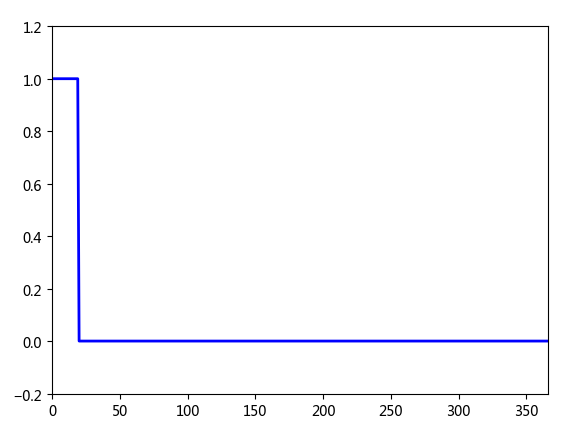
部分代码：

# 定义函数，显示滤波器模板
def showTemplate(template):
    temp = np.uint8(template*255)
    cv2.imshow('Template', temp)
    return


# 定义函数，显示滤波函数
def showFunction(template):
    row, col = template.shape
    row = np.uint16(row/2)
    col = np.uint16(col/2)
    y = template[row, col:]
    x = np.arange(len(y))
    plt.plot(x, y, 'b-', linewidth=2)
    plt.axis([0, len(x), -0.2, 1.2])
    plt.show()
    return


# 定义函数，理想的低通/高通滤波模板
def Ideal(src, d0, ftype):
    template = np.zeros(src.shape, dtype=np.float32)  # 构建滤波器
    r, c = src.shape
    for i in range(r):
        for j in range(c):
            distance = np.sqrt((i - r/2)**2 + (j - c/2)**2)
            if distance < d0:
                template[i, j] = 1
            else:
                template[i, j] = 0

    if ftype == 'high':
        template = 1 - template
    return template

 2. Butterworth高/低通滤波

Butterworth低通滤波器函数为：

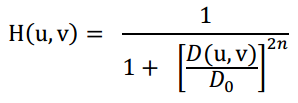
从函数图上看，更圆滑，用幂系数n可以改变滤波器的形状。n越大，则该滤波器越接近于理想滤波器

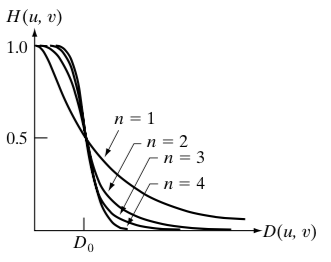
 1减去低通滤波模板即可得到高通滤波模板

 

部分代码：

# 定义函数，巴特沃斯高/低通滤波模板
def Butterworth(src, d0, n, ftype):
    template = np.zeros(src.shape, dtype=np.float32)  # 构建滤波器
    r, c = src.shape
    for i in np.arange(r):
        for j in np.arange(c):
            distance = np.sqrt((i - r/2)**2 + (j - c/2)**2)
            template[i, j] = 1/(1 + (distance/d0)**(2*n))  # Butterworth 滤波函数
            template[i, j] = np.e ** (-1 * (distance**2 / (2 * d0**2)))  # Gaussian滤波函数
    if ftype == 'high':
        template = 1 - template
    return template

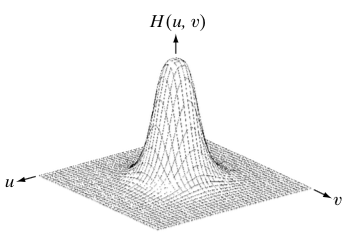
 3. Gaussian高/低通滤波

Guassian低通滤波器函数为：

 

 1减去低通滤波模板即可得到高通滤波模板

 

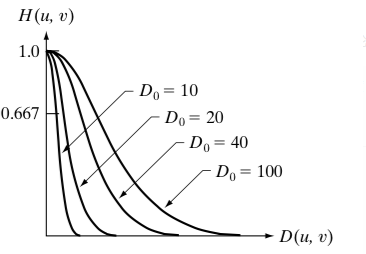
 部分代码：

# 定义函数，高斯高/低通滤波模板
def Gaussian(src, d0, ftype):
    template = np.zeros(src.shape, dtype=np.float32)  # 构建滤波器
    r, c = src.shape
    for i in np.arange(r):
        for j in np.arange(c):
            distance = np.sqrt((i - r / 2) ** 2 + (j - c / 2) ** 2)
            template[i, j] = np.e ** (-1 * (distance ** 2 / (2 * d0 ** 2)))  # Gaussian滤波函数
    if ftype == 'high':
        template = 1 - template
    return template