数字图像处理-空间域处理-直方图均衡化

直方图均衡化一来可以提高图像的对比度，二来可以把图像变换成像素值是几乎均匀分布的图像。其中心思想是把原始图像的灰度直方图从比较集中的某个灰度区间变成在全部灰度范围内的均匀分布。

我们知道灰度值分布较为平均的图像，通常对比度较高。直方图均衡化就是对图像进行非线性拉伸，重新分配图像像素值，使一定灰度范围内的像素数量大致相同的过程。

                                                        

原理

作者：王彦恒
来源：知乎
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

为简化问题，仅讨论灰度图像的直方图均衡。

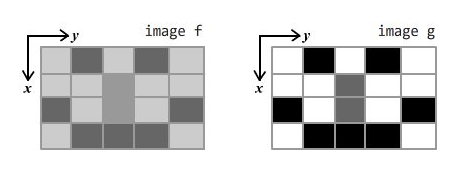
设输入图像为二元函数 f(x, y) ，输出图像为二元函数 g(x, y)，显然二者尺寸相等。我们知道，那些灰度值分布较为平均的图像，通常对比度较高。比如，下图中 g 的灰度较分散（有白的有灰的有黑的），所以对比度较高；f 的灰度很集中，所以显得灰蒙蒙的。直方图均衡的目的，就是对 f 进行处理产生 g，使得 g 的灰度值比 f 更分散。

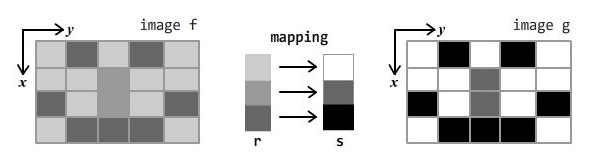
怎么做呢？如果我们有一个恰当的 灰度映射函数 T 就好了，它能把输入灰度值 r 映射为输出灰度值为 s，即 s = T(r) 。假设图像的灰度值连续，由黑到白取值为1～L中的实数。灰度映射函数 T 可能长这样：

s = T(r) = \begin{cases} 1, &r \in [1, \frac{L}{4}] \cr 2r - \frac{L}{2}, &r \in [\frac{L}{4}, \frac{3L}{4}] \cr L, &r \in [\frac{3L}{4} , L] \end{cases}

用图形来表达就是：

对图像施以该灰度映射，图示如下：

看起来不错。不过——有一句老话叫做“具体问题具体分析”，这告诉我们：决不可能使用某个特定的 T 一劳永逸。那么，有没有办法“自动地”根据实际情况生成 T 呢？答案是肯定的。请接着往下看。

设任意灰度值 t 在 f 中出现的概率为函数 p_f(t) ，在 g 中出现的概率为函数 p_g(t) 。这两个函数均可以直接由图像统计出来。然后，我们定义两个函数

S_f(n) = \int_{1}^{n}p_f(t)dt （意义：f 中灰度值小于 n 的概率）

以及

S_g(n) = \int_{1}^{n}p_g(t)dt （意义：g 中灰度值小于 n 的概率）

那么必然有

S_f(r) = S_g[T(r)] \Leftrightarrow S_f(r) = S_g(s) \ \ \cdots \cdots(1)

为什么呢？这是因为我们必须保证：原本比 r 暗的灰度，在变换后依然比 s 暗；原本比 r 亮的灰度，在变换后依然比 s 亮。如果连这一点都不能保证，那么输出的图像就会黑白颠倒一团糟。

比方说，若 r = 1/3 ，变换后 s = T(r) = 5/2。那么，f 中灰度值小于1/3的像素数目 ＝＝ g 中灰度值小于5/2的像素数目。用频率估算概率，也就是 f 中灰度值小于1/3的概率 ＝＝ g 中灰度值小于5/2的概率。还不懂？看图！

弄清楚上面的式子后，自然得到下面的式子（积分后就等于(1) ）：

p_f(r) \cdot dr = p_g(s) \cdot ds \ \ \cdots\cdots (2)

再接下来，如果我们令变换 T(r) = L \cdot S_f(r) ，那么：

\begin{align} s &= T(r) \\ &= L \cdot S_f(r)\\ &= L \cdot \int_{1}^{r}p_f(t)dt \\ \Rightarrow \frac{ds}{dr} &= L \cdot p_f(r) \ \ \cdots \cdots (3) \end{align}

其中的第三行，t 是积分变量，真正的自变量是积分上限 r。

由 (2)(3) 得

p_g(s) = 1/L

奇迹出现了：g 中各灰度出现概率相等，为常数1/L。也就是说，各灰度被完全均摊了！

于是我们知道，无论输入图像是什么，只要统计它之中各灰度值出现的概率 p_f ，然后生成映射函数 T(r) = L \cdot S_f(r) = L \cdot \int_{1}^{r} p_f(t)dt ，剩下的事就是逐个映射图中灰度即可。

 

现实中数字图像的灰度值是离散的，对此我们只需略作修改。假设图像最多含有 L 种灰度级，由黑到白依次编号为 1, 2, \cdots, L 。每个灰度级在 f 中出现的概率依次为p_f(1), p_f(2), \cdots, p_f(L) ，在 g 中出现的概率依次为 p_g(1), p_g(2), \cdots, p_g(L) 。

函数定义改为： S_f(n) = \sum_{i=1}^{n}{p_f(i)} 以及 S_g(n) = \sum_{i=1}^{n}{p_g(i)} ，其余同理。

可惜的是，在灰度值离散的情况下，r 和 s 均为整数，我们必须对映射结果取整，这导致 g 中各灰度值出现的概率未必相等。但是可以确定的是： g 的灰度级在一定程度上比 f 更分散了。

 

为什么是累积分布函数？

直方图均衡要保证两点：

1、函数映射要保证原图像的大小关系不变。亮区域变换后依然1亮，暗区域变换后依然暗，只是对比度增强了。要保证这一点，映射函数必须单调递增。累积分布函数单调递增。

2、映射范围，原图像[0, 255]，新图像的范围也要[0, 255]，不能超出。累积分布函数值域为[0, 1]可以很好的控制范围。

 

为什么均衡化后灰度分布是均匀的？

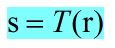映射函数　　r为输入灰度值，s为输出灰度值

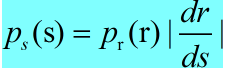概率密度函数　　由基本概率论得：如果Pr(r)和T(r)已知，且在感兴趣的值域上T(r)是连续且可微的，则映射后s的概率密度函数由上式计算。其中：Pr(r)为输入灰度值r的概率密度函数，Ps(s)为输出灰度值s的概率密度函数

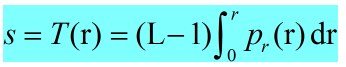直方图均衡函数

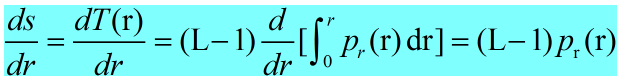推导1

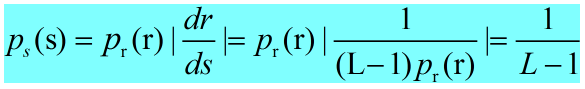推导2

奇迹出现了，Ps(s)是一个常数，也就是说映射后的新图像概率密度是均匀的，即对比度高。当然这是从结果来推条件了，这样也是为了更容易理解。

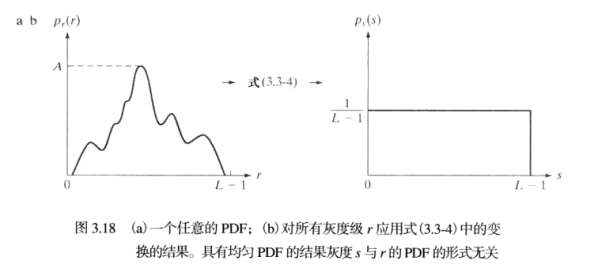
　　　　　　　　　　　　　　　　实际没这么夸张，一般无法均匀成一条直线

 

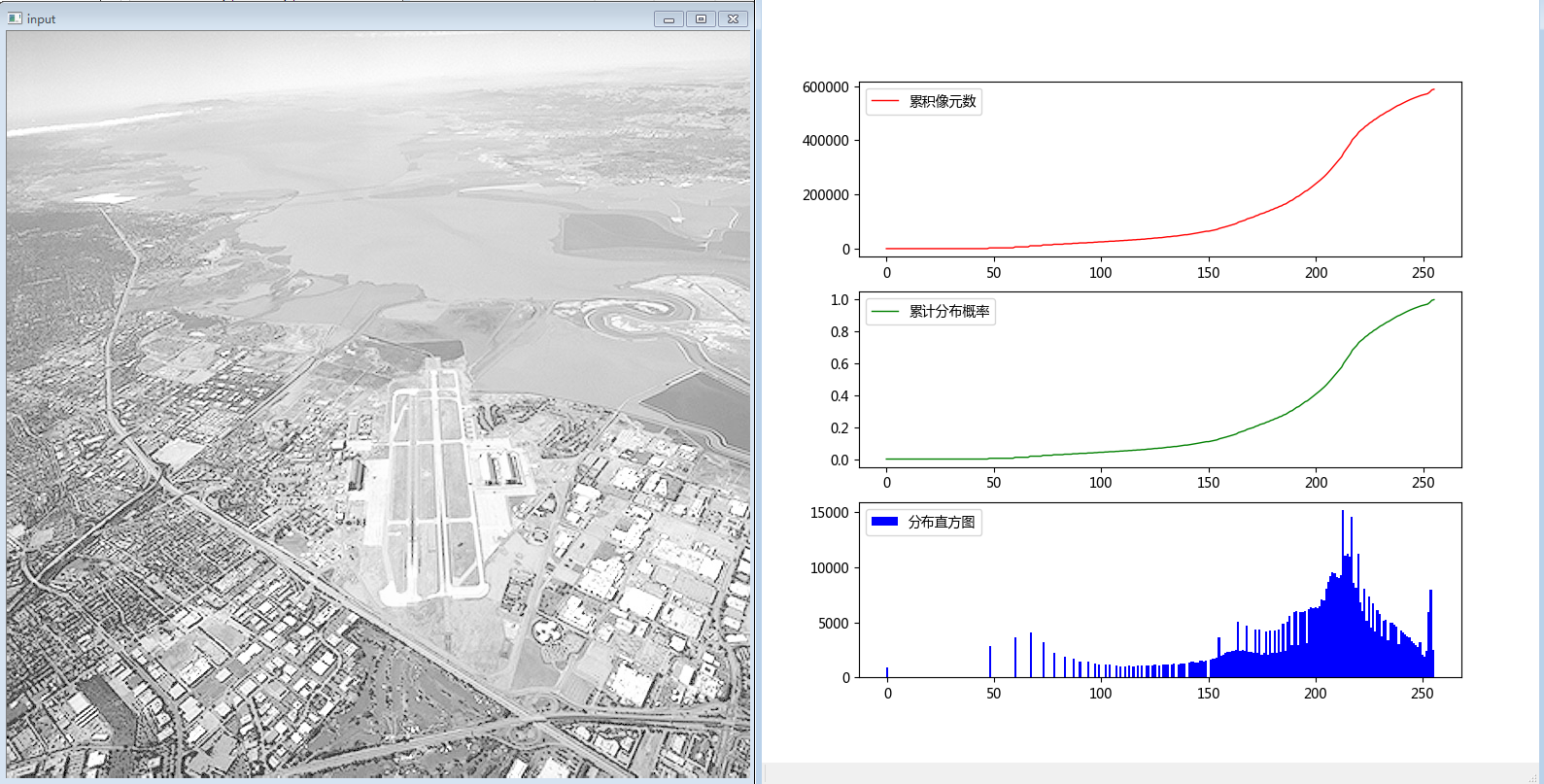
假设有如下图像：

得图像的统计信息如下图所示，并根据统计信息完成灰度值映射：

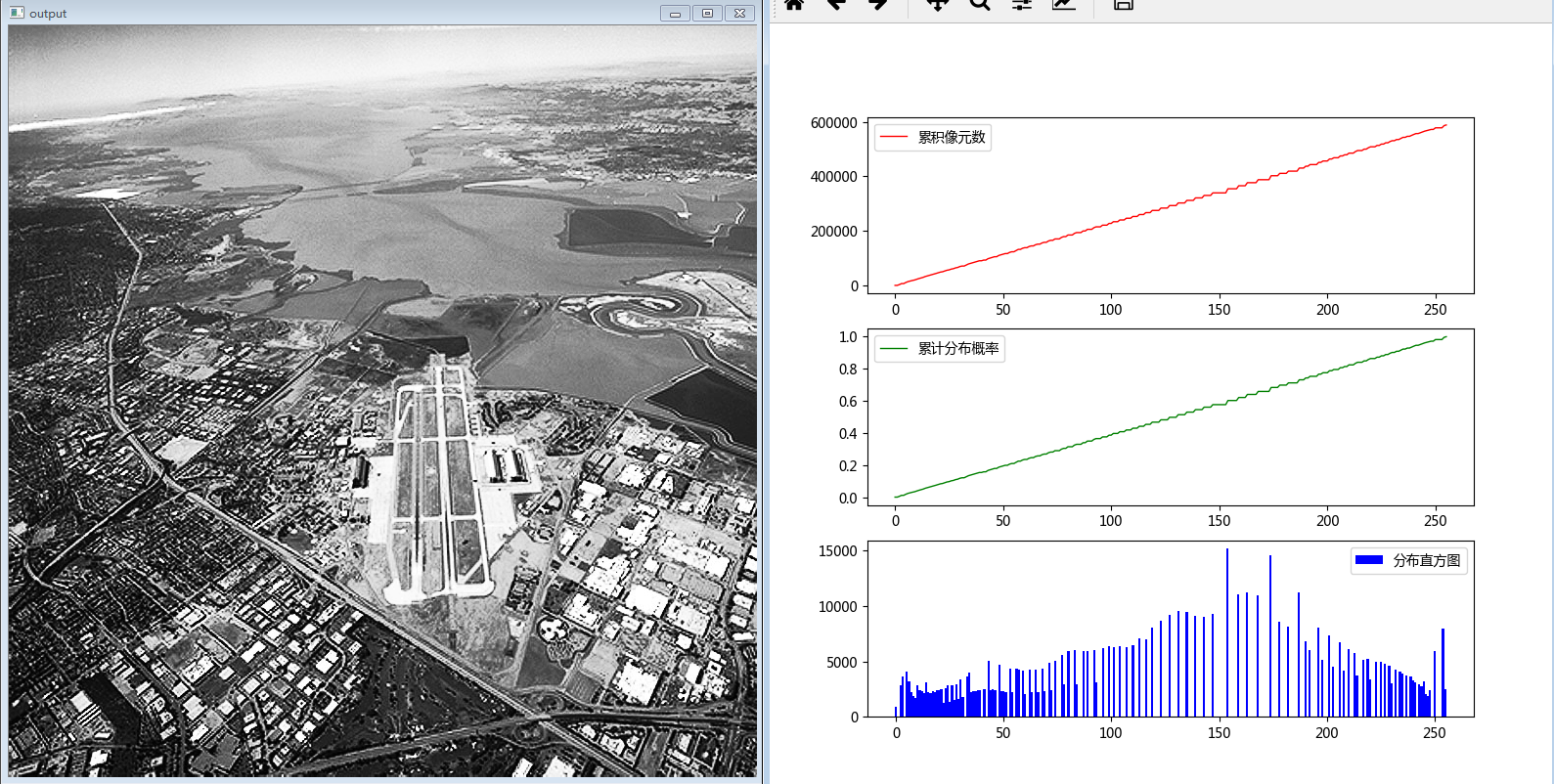
映射后的图像如下所示：

 

 

直方图均衡化的映射方程为s = L*T(r)    其中s为映射后的灰度值，L为灰度级8比特255，T(r)为灰度值r的累积分布概率，由分布概率计算得到，分布概率由灰度值r的像元数 / 总像元数得到

 

实战

"""直方图均衡化"""
import matplotlib.pyplot as plt
import numpy as np
import cv2


# 定义函数，实现图像直方图，累积像元数图和累积分布概率图绘制
def histPlot(hist, cumhist):
    plt.figure('辅助图', figsize=(8, 8))
    DN = np.arange(256)

    plt.subplot(311)
    plt.plot(DN, cumhist, 'r', linewidth=1, label='累积像元数')
    plt.legend(loc='best')

    plt.subplot(312)
    plt.plot(DN, cumhist/(769*765), 'g', lw=1, label='累计分布概率')  # 769*765为图像行列数，此处投机取巧，无普适性
    plt.legend(loc='best')

    plt.subplot(313)
    plt.bar(DN, hist, color='b', width=1, label='分布直方图')
    plt.legend(loc='best')

    plt.show()
    return


# 定义函数，实现图像的直方图均衡化
def histEqualization(src):
    row, col = src.shape
    hist, cumhist = histStatistics(src)
    # 生成查找表进行直方图均衡化
    lut = np.zeros(256, dtype=np.float32)
    for i in range(256):
        lut[i] = 255.0/(row*col) * cumhist[i]  # 均衡化的公式cunhist[i]/(row*col)为累积概率
    lut = np.uint8(lut + 0.5)
    dst = cv2.LUT(src, lut)
    return dst


# 定义函数，实现图像直方图统计
def histStatistics(src):
    row, col = src.shape
    hist = np.zeros(256, dtype=np.float32)
    cumhist = np.zeros(256, dtype=np.float32)
    for i in np.arange(row):
        for j in np.arange(col):
            hist[src[i, j]] += 1
    cumhist[0] = hist[0]
    for i in range(1, 256):
        cumhist[i] = cumhist[i - 1] + hist[i]
    histPlot(hist, cumhist)
    return hist, cumhist


img = cv2.imread('F:\program_study\Python\data\city.tif', cv2.IMREAD_GRAYSCALE)
cv2.imshow('input', img)

imgOutput = histEqualization(img)
cv2.imshow('output', imgOutput)
histStatistics(imgOutput)

cv2.waitKey(0)
cv2.destroyAllWindows()

 

posted @ 2018-01-12 14:07  Laumians  阅读(879)  评论(0)  编辑  收藏  举报