矩阵分解在推荐系统中的应用及实践
完整代码地址 ? https://github.com/DL-Metaphysics/APR/blob/master/MF/MF.ipynb
推荐系统的研究从上世纪90年代初发展至今,目前有三大主流算法作为几乎全部的推荐算法的基石,它们就是基于内容的过滤算法(content-based filtering,简称CBF)、邻域算法(neighborhood methods)、隐语义模型(latent factor models,简称LFM),其中后两者统称为协同过滤算法(collaborative filtering,简CF)。
CBF通过给用户、物品定义显式的属性(通常会找所涉及的推荐领域的人类专家来定义)来描述他们的本质,然后为用户推荐与他们本质“门当户对”的物品;CF则是通过发动“群体的力量”,从其他用户、物品中学习到宝贵的信息,无需显式地定义属性:CF下的邻域算法着重于学习用户与用户、物品与物品之间的关系,为目标用户推荐与目标用户相似的用户所选择的物品(user-based)或者与目标用户所选择的物品相似的物品(item-based);CF下的隐语义模型则是通过学习用户与用户、物品与物品之间的关系来自动获得用户、物品的隐属性(这里的“隐”指的是学习到的属性是不可解释的),相当于把用户-评分矩阵分解成用户隐属性矩阵和物品隐属性矩阵,然后通过用户隐属性向量u与物品隐属性向量i作点乘来获取到该用户对该物品的评分,以此为依据进行推荐。

矩阵分解的主要思想
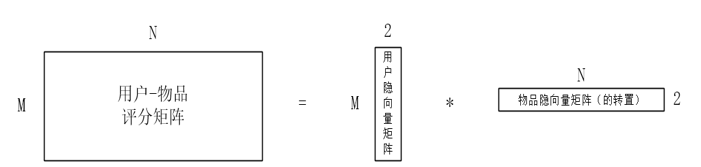
如上图所示,矩阵分解是构建隐语义模型的主要方法,即通过把整理、提取好的“用户—物品”评分矩阵进行分解,来得到一个用户隐向量矩阵和一个物品隐向量矩阵。
假设现在有一个
M
∗
N
M*N
M∗N 的矩阵,
M
M
M 代表用户数,
N
N
N 代表物品数,想将用户、物品分别训练出两个隐属性,即每个用户、每个物品都对应着一个二维向量,即得到了一个
M
2
M2
M2 的用户隐向量矩阵和一个
N
2
N2
N2 的矩阵,分解示意图如下所示:
在得到用户隐向量和物品隐向量(均是2维向量)之后,我们可以将每个用户、物品对应的二维隐向量看作是一个坐标,将其画在坐标轴上。虽然我们得到的是不可解释的隐向量,但是可以为其赋予一定的意义来帮助我们理解这个分解结果。比如我们把用户、物品的2维的隐向量赋予严肃文学(Serious)vs.消遣文学(Escapist)、针对男性(Geared towards males)vs.针对女性(Geared towards females),那么可以形成如下图的可视化图片:
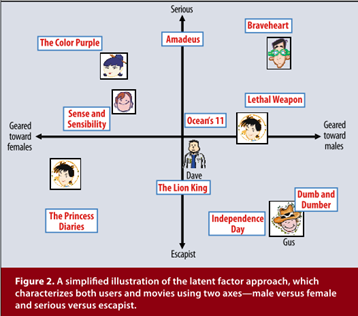
从上图我们可以看到,用户对于与其处于同一象限的物品的喜爱度/评分是会很高的,因为他们相比于其它的组合更加“门当户对”一些。而实例人物Dave对应的坐标恰好处于坐标系的中央,这说明他对图中所有物品的喜爱程度差不多,没有特别喜欢的也没有特别讨厌的。
矩阵分解中的显式反馈与隐式反馈
推荐系统、推荐算法的设计依赖于多种输入。在上部分中,我们针对用户—物品评分矩阵来对其进行分解,得到了两个隐向量矩阵。这里我们用到的输入就是这个评分矩阵。在推荐系统中,用户的评分信息输入最重要的输入信息,也是一种显式反馈。不过,显式反馈的信息往往是很稀有的,也就是说我们要分解的评分矩阵往往是一个很稀疏的矩阵,可能里面 70% 以上的元素都是 0,只有 30% 的部分是稀稀落落的评分,所以单纯地依赖显式反馈信息在如今会得到正确率较低的推荐结果。不过矩阵分解的好处在于,它可以融入多种额外的信息。用户的购买、浏览、点击行为虽然不如评分那样有着很大的信息量,但是也是一种隐式反馈的信息,利用好它们,我们可以组成一个很稠密的矩阵,以此来改良推荐结果。
矩阵分解过程
完整代码地址 ? https://github.com/DL-Metaphysics/APR/blob/master/MF/MF.ipynb
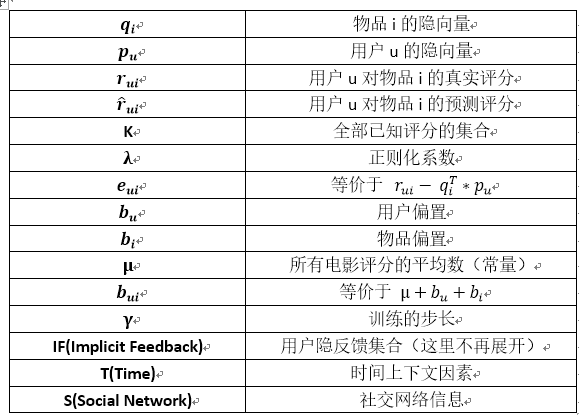
先把之后需要用到的全部的数学符号或者缩略语都统一列到下表中:
如前面所介绍的,矩阵分解可以融入多种额外信息,不断地对待分解矩阵进行升级、改良,整体的矩阵分解框架如下图所示:

我们首先看一下没有融合额外信息的时候,是如何来预测评分的:
r ^ u i = q i T ∗ p u \hat{r}_{u i}=q_{i}^{T} * p_{u} r^ui=qiT∗pu
可以看出,其实很简单的。当我们要预测 u 对 i 评分的时候,就直接把对应的用户隐向量、物品隐向量直接点乘起来就好了,就得到预测的评分了。但是这两个矩阵是怎么来的呢?当然是训练出来的啦,我们要通过优化下面这个目标函数来训练出这两个矩阵,这就是标准的“机器学习版”的矩阵分解算法,也是推荐系统领域非常重要的算法:
min q ∗ , p ∗ ∑ ( u , i ) ∈ K ( r u i − q i T ∗ p u ) 2 + λ ∗ ( ∥ q i ∥ 2 + ∥ p u ∥ 2 ) \min _{q^{*}, p^{*}} \sum_{(u, i) \in K}\left(r_{u i}-q_{i}^{T} * p_{u}\right)^{2}+\lambda *\left(\left\|q_{i}\right\|^{2}+\left\|p_{u}\right\|^{2}\right) q∗,p∗min(u,i)∈K∑(rui−qiT∗pu)2+λ∗(∥qi∥2+∥pu∥2)
我们采用随机梯度下降(SGD)算法来训练两个隐向量矩阵:
q i = q i + γ ∗ ( e u i ∗ p u − λ ∗ q i ) p u = p u + γ ∗ ( e u i ∗ q i − λ ∗ p u ) \begin{aligned} q_{i} &=q_{i}+\gamma *\left(e_{u i} * p_{u}-\lambda * q_{i}\right) \\ p_{u} &=p_{u}+\gamma *\left(e_{u i} * q_{i}-\lambda * p_{u}\right) \end{aligned} qipu=qi+γ∗(eui∗pu−λ∗qi)=pu+γ∗(eui∗qi−λ∗pu)
整个SGD的函数代码如下所示:
def sgd(data_matrix, user, item, alpha, lam, iter_num):
for j in range(iter_num):
for u in range(data_matrix.shape[0]):
for i in range(data_matrix.shape[1]):
if data_matrix[u][i] != 0:
e_ui = data_matrix[u][i] - sum(user[u,:] * item[i,:])
user[u,:] += alpha * (e_ui * item[i,:] - lam * user[u,:])
item[i,:] += alpha * (e_ui * user[u,:] - lam * item[i,:])
return user, item
这样我们就训练出了两个隐向量矩阵,将他们相乘便得到了预测版的评分矩阵,可以和真实评分矩阵对比一下,如果训练的次数足够,训练步长不大的话其实预测的评分已经比较准了。
但是,有一个问题我们需要考虑一下。如果有的用户比较苛刻,对他来说,烂片最多打1分,好的片子也就得3-4分,有的用户比较宽容,他认为人家拍个电影挺不容易的,烂片也给了3分,好的片子一律给5分,那对于这两种用户,我们要采取同样的对待方式进行预测吗?如果有的电影拍的真心好,普遍评分都很高,有的电影烂出了新高度,基本上上3分那都是绝对的高分了,那这两种电影真的都处于0-5分这一分段吗?
在这种情况下,我们其实需要为每个用户和每个物品加入一些偏置元素 bu 和 bi,代表了他们自带的与其他事物无关的属性,融入了这些元素,才能区别且正确地对待每一个用户和每一个物品,才能在预测中显得更加个性化。所以,预测评分的计算公式就变成了这样:
r ^ u i = b u i + q i T ∗ p u \hat{r}_{u i}=b_{u i}+q_{i}^{T} * p_{u} r^ui=bui+qiT∗pu
我们要优化、训练参数的目标公式也就变成了下图所示,要训练的参数除了用户、物品隐向量还要加上用户、物品偏置值,训练的方法同样是采用随机梯度下降法:
min q ∗ , p ∗ ∑ ( u , i ) ∈ K ( r u i − b u i − q i T ∗ p u ) 2 + λ ∗ ( ∥ q i ∥ 2 + ∥ p u ∥ 2 + b u 2 + b i 2 ) \min _{q^{*}, p^{*}} \sum_{(u, i) \in K}\left(r_{u i}-b_{u i}-q_{i}^{T} * p_{u}\right)^{2}+\lambda *\left(\left\|q_{i}\right\|^{2}+\left\|p_{u}\right\|^{2}+b_{u}^{2}+b_{i}^{2}\right) q∗,p∗min(u,i)∈K∑(rui−bui−qiT∗pu)2+λ∗(∥qi∥2+∥pu∥2+bu2+bi2)
整个SGD_bias的函数的代码如下所示:
def sgd_bias(data_matrix, user, item, alpha, lam, iter_num, miu):
b_u = [1] * rating_matrix.shape[0]
b_i = [1] * rating_matrix.shape[1]
for j in range(iter_num):
for u in range(data_matrix.shape[0]):
for i in range(data_matrix.shape[1]):
if data_matrix[u][i] != 0:
b_ui = b_u[u] + b_i[i] + miu
e_ui = data_matrix[u][i] - b_ui - sum(user[u,:] * item[i,:])
user[u,:] += alpha * (e_ui * item[i,:] - lam * user[u,:])
item[i,:] += alpha * (e_ui * user[u,:] - lam * item[i,:])
b_u[u] += alpha * (e_ui - lam * b_u[u])
b_i[i] += alpha * (e_ui - lam * b_i[i])
return user, item, b_u, b_i
在加入偏置后,预测的就更加准确一些了。在编程实验中,笔者采用了推荐系统算法常见的评测标准——MSE来进行两种分解算法的评测,两者的结果如下所示(注:训练步长0.001,正则化系数0.1,训练次数:1000次):




