2020最终数学杯 初级组第3题

试题来源：https://artofproblemsolving.com/community/c1332626

 

给定正整数k．求n的最小值(1<k<n)，使得可以对一个n×n的网格表进行染色，令其每行和每列中都恰有k个黑色单元格.并给出一个示例。

`

`

`

`

`

`

`

`

`

`

`

`

`

`

解答：因为k<n，所以n>=k+1。下面证明n的最小值就是k+1。

 

 

 当n=k+1时，假设存在满足题意的染色方法，那么对于任意一种满足题意的染色方法都可通过交换列的方式使第一行变成上图的形式且不会造成任何影响。那么对最后一列来说，必然是下图这种情况：

 

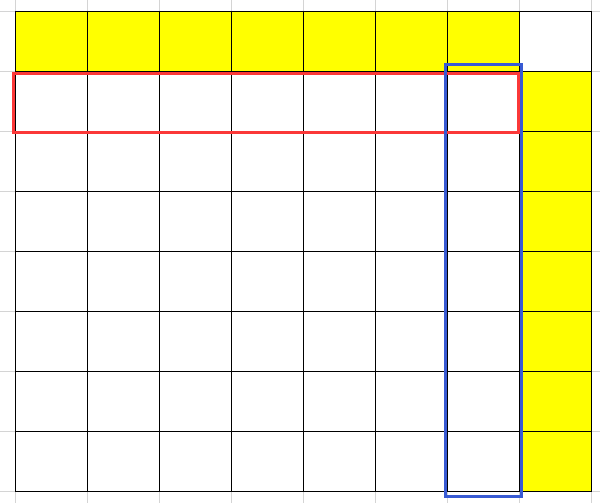
 经分析可知红色、蓝色框里只能有一个空白格子，不妨让两个框里重叠的那个格子为空白，则：

 

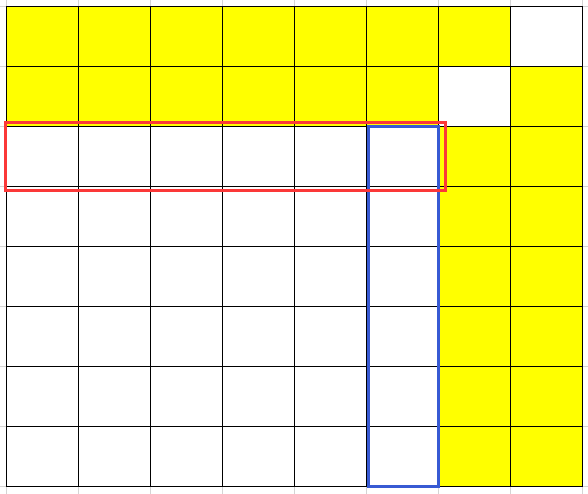
 上图红色、蓝色框里也只能有一个空白格子，不妨让两个框里重叠的那个格子为空白，那么有：

 

 

 一直采取这种方式分析，那么最后有：

 

 显然这是一种有效的染色方式。

综上，n的最小值为k+1。