数学竞赛 组合类问题（1）

在单位正方形周界上的两个点连接一条直线，如果这条直线把正方形分成面积相等的两部分，试证该直线长度不小于1

 

证明：该题非常简单。先证明这条直线必然过正方形中心点O：

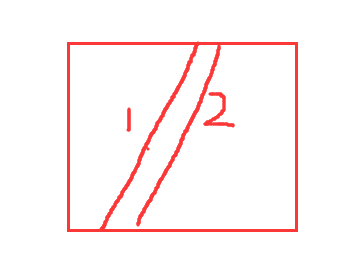假设1线不过中心点O且分成面积相等的两部分，过O作平行于1的直线2，易知2将正方形分成S=的两部分，所以1肯定没把正方形分成S=的两部分，与假设矛盾，所以这条直线必然过正方形中心点O。而过O点且两端点在正方形周界上的线段的长度不小于一，所以命题得证。