2022GDUT寒训专题五
树状数组
简要介绍
树状数组其实是通过维护不同长度的区间和来达到O(logn)级别的点修改和区间查询。
主要是利用了lowbit 函数,其实是非常简单滴。qvq
支持的功能
1、单点修改和区间查询
2、区间修改和单点查询(利用差分)
3、区间修改和区间查询(利用差分+公式变形)
板子
单点修改和区间查询
#include <bits/stdc++.h>
#define SF ios_base::sync_with_stdio(false);cin.tie(NULL);cout.tie(NULL);
#define ms(x, y) memset(x, y, sizeof(x))
#define INF 0x3f3f3f
#define X first
#define Y second
using namespace std;
typedef pair<int, int> PII;
typedef long long ll;
typedef long double ld;
const int maxn = 5e5 + 10;
//树状数组单点修改和区间查询板子
//最基础的用法啦
int n, m;
int tree[maxn];
int lowbit(int a) {return a&(-a);}
void update(int x, int k){
for(;x <= n;x += lowbit(x)){
tree[x] += k;
}
}
ll getsum(int x){
ll sum = 0;
for(;x >= 1; x -= lowbit(x)){
sum += tree[x];
}
return sum;
}
int main(){
SF
cin >> n >> m;
for(int i = 1;i <= n;++i){
int temp;cin >> temp;
update(i, temp);
}
for(int i = 1;i <= m;++i){
int op;cin >> op;
if(op == 1){
int x, k;cin >> x >> k;
update(x, k);
}else{
int l, r;cin >> l >> r;
cout << getsum(r) - getsum(l-1) << endl;
}
}
return 0;
}
区间修改和单点查询
#include <bits/stdc++.h>
#define SF ios_base::sync_with_stdio(false);cin.tie(NULL);cout.tie(NULL);
#define ms(x, y) memset(x, y, sizeof(x))
#define INF 0x3f3f3f
#define X first
#define Y second
using namespace std;
typedef pair<int, int> PII;
typedef long long ll;
typedef long double ld;
const int maxn = 5e5 + 10;
//树状数组区间修改+单点查询的板子
//所以利用差分,将区间修改变成单点修改, 将单点查询变成区间查询就又可以用最基础的树状数组模板了耶
//维护差分数组就好咯
int n, m;
int aa[maxn];
int tree[maxn];
int lowbit(int a) {return a&(-a);}
void update(int x, int k){
for(;x <= n;x += lowbit(x)){
tree[x] += k;
}
}
ll getsum(int x){
ll sum = 0;
for(;x >= 1; x -= lowbit(x)){
sum += tree[x];
}
return sum;
}
int main(){
SF
cin >> n >> m;
for(int i = 1;i <= n;++i){
cin >> aa[i];
}
for(int i = 1;i <= n;++i){
int temp = aa[i] - aa[i-1];
update(i, temp);
}
for(int i = 1;i <= m;++i){
int op;cin >> op;
if(op == 1){
int x, y, k;cin >> x >> y >> k;
update(x, k);
update(y+1, -k);
}else{
int num;cin >> num;
cout << getsum(num) << endl;
}
}
return 0;
}
区间修改和区间查询
#define SF ios_base::sync_with_stdio(false);cin.tie(NULL);cout.tie(NULL);
#define ms(x, y) memset(x, y, sizeof(x))
#define INF 0x3f3f3f
#define X first
#define Y second
using namespace std;
typedef pair<int, int> PII;
typedef long long ll;
typedef long double ld;
const int maxn = 5e5 + 10;
//树状数组区间修改+区间查询板子
//求p位置的前缀和实际上就是: (p+1)∗∑_{i=1}^{p}d[i]−∑_{i=1}^{p}d[i]∗i
//所以实际上我们是在维护差分数组aa和bb数组:(aa*i)
ll n, m;
ll num[maxn];
ll aa[maxn];
ll bb[maxn];
ll lowbit(ll a) {return a&(-a);}
void update(ll x, ll k){
for(int i = x;i <= n;i += lowbit(i)){
aa[i] += k;
bb[i] += x*k;
}
}
void range_update(ll x, ll y, ll k){
update(x, k);
update(y+1, -k);
}
ll getsum(ll x){
ll sum = 0;
for(int i = x;i >= 1; i -= lowbit(i)){
//单点的前缀和答案是这个
sum += (x+1)*aa[i] - bb[i];
}
return sum;
}
ll range_sum(ll x, ll y){
return getsum(y) - getsum(x-1);
}
int main(){
SF
cin >> n >> m;
for(int i = 1;i <= n;++i){
cin >> num[i];
}
for(int i = 1;i <= n;++i){
ll temp = num[i]-num[i-1];
update(i, temp);
}
//以上为输入处理
for(int i = 1;i <= m;++i){
int op;cin >> op;
if(op == 1){
ll x, y, k;cin >> x >> y >> k;
range_update(x, y, k);
}else {
ll x, y;cin >> x >> y;
cout << range_sum(x, y) << endl;
}
}
return 0;
}
线段树
简要介绍
线段树实际上是利用一个完美二叉树来维护多个子区间和以达到O(logn)级别的修改和查询的数据结构。
相比于树状数组,适用范围更广,更灵活多变
有趣的地方
精髓在于lazy标记,每次只更新需要用到的区间和就好了
让我想到并查集的路径压缩~
板子
单点修改和区间查询
#include <bits/stdc++.h>
//#pragma comment(linker, "/STACK:102400000,102400000")//手动开大栈区
#define SF ios_base::sync_with_stdio(false);cin.tie(NULL);cout.tie(NULL);
#define ms(x, y) memset(x, y, sizeof(x))
#define INF 0x3f3f3f
#define X first
#define Y second
using namespace std;
typedef pair<int, int> PII;
typedef long long ll;
typedef long double ld;
const int maxn = 5e5+10;
//线段树单点修改区间查询的板子
//记住这个tr数组要开四倍空间
//简单介绍下线段树思路,其实就是维护多个子区间
int aa[maxn];
struct node{
int l, r, sum;
}tr[maxn << 2];
//用子节点向上更新父节点
void pushup(int u){
tr[u].sum = tr[u<<1].sum + tr[u<<1|1].sum;
}
//这里建树的过程实际上是找到最低层,然后自底向上递归建树
void bt(int u, int l, int r){
if(l == r) {
tr[u] = {l, r, aa[l]};
}else{
tr[u] = {l, r};
int mid = l+r >> 1;
bt(u<<1, l, mid);
bt(u<<1|1, mid+1, r);
pushup(u);
}
}
//这边更新的话也是找到该点,然后自底向上更新
void update(int u, int x, int d){
if(x == tr[u].l && x == tr[u].r){
tr[u].sum += d;
}else{
int mid = tr[u].l + tr[u].r >> 1;
//这个地方只可能是左子树或者是右子树
if(x <= mid) update(u<<1, x, d);
else update(u<<1|1, x, d);
pushup(u);
}
}
//询问的话就是找到能被区间l,r完全包含的区间就加入答案中。
int query(int u, int l, int r){
if(l <= tr[u].l && tr[u].r <= r){
return tr[u].sum;
}else{
int mid = tr[u].l + tr[u].r >> 1;
int ret = 0;
//这个地方有可能既往左又往右递归,不过只可能有一次存在这样的情况。也就是第一次
if(l <= mid) ret += query(u<<1, l, r);
if(r > mid) ret += query(u<<1|1, l, r);
return ret;
}
}
int main(){
SF
int n, m;cin >> n >> m;
for(int i = 1;i <= n;++i) cin >> aa[i];
//一定要记得先建树!!> ^ <
bt(1, 1, n);
while(m--){
int op;cin >> op;
if(op == 1){
int x, k;cin >> x >> k;
//从根结点开始找
update(1, x, k);
}else {
int l, r;cin >> l >> r;
int ans = query(1,l ,r);
cout << ans << endl;
}
}
return 0;
}
区间修改和区间查询
#include <bits/stdc++.h>
//#pragma comment(linker, "/STACK:102400000,102400000")//手动开大栈区
#define SF ios_base::sync_with_stdio(false);cin.tie(NULL);cout.tie(NULL);
#define ms(x, y) memset(x, y, sizeof(x))
#define INF 0x3f3f3f
#define X first
#define Y second
using namespace std;
typedef pair<int, int> PII;
typedef long long ll;
typedef long double ld;
const int maxn = 5e5+10;
//线段树区间修改和区间查询的板子
//主要看这个lazy标记和PushDown操作
struct node{
int l, r;
ll sum;
ll lazy;
}tr[maxn << 2];
ll aa[maxn];
void PushUp(int u) {tr[u].sum = tr[u<<1].sum + tr[u<<1|1].sum;}
void Build(int u, int l, int r){
if(l == r) {
tr[u] = {l, r, aa[l]};
}else{
tr[u] = {l, r};
int mid = l+r>>1;
Build(u<<1, l, mid);
Build(u<<1|1, mid+1, r);
PushUp(u);
}
}
//将标记下推,并清空本层标记
void PushDown(int u){
if(tr[u].lazy != 0){
tr[u<<1].lazy += tr[u].lazy;
tr[u<<1|1].lazy += tr[u].lazy;
tr[u<<1].sum += tr[u].lazy*(tr[u<<1].r-tr[u<<1].l+1);
tr[u<<1|1].sum += tr[u].lazy*(tr[u<<1|1].r-tr[u<<1|1].l+1);
tr[u].lazy = 0;
}
}
//在更新时仅更新到刚好符合条件的区间,但在更底层的区间就没有被标更新到了
//所以在当前一层的元素打上标记,当下次查询到或者是用到该区间的时候才更新
void Update(int u, int L, int R, int c){
if(L <= tr[u].l && tr[u].r <= R){
//当前走到的区间实际上已经是更新过的
tr[u].sum += c*(tr[u].r-tr[u].l+1);
tr[u].lazy += c;
return ;
}
PushDown(u);
int mid = tr[u].l+tr[u].r >> 1;
if(L <= mid) Update(u<<1, L, R, c);
if(R > mid) Update(u<<1|1, L, R, c);
PushUp(u);
}
ll Query(int u, int L, int R){
if(L <= tr[u].l && tr[u].r <= R){
return tr[u].sum;
}
int mid = tr[u].l+tr[u].r >> 1;
//这个地方也需要PushDown,不然答案会出错
PushDown(u);
ll ret = 0;
if(L <= mid) ret += Query(u<<1, L, R);
if(R > mid) ret += Query(u<<1|1, L, R);
return ret;
}
int main(){
SF
int n, m;cin >> n >> m;
for(int i = 1;i <= n;++i) cin >> aa[i];
Build(1, 1, n);
while(m--){
int op; cin >> op;
if(op == 1){
int l, r, k;cin >> l >> r >> k;
Update(1, l, r, k);
}else{
int l, r;cin >> l >> r;
ll ans = Query(1, l, r);
cout << ans << endl;
}
}
return 0;
}
区间乘法和区间加法
#include <bits/stdc++.h>
//#pragma comment(linker, "/STACK:102400000,102400000")//手动开大栈区
#define SF ios_base::sync_with_stdio(false);cin.tie(NULL);cout.tie(NULL);
#define ms(x, y) memset(x, y, sizeof(x))
#define INF 0x3f3f3f
#define X first
#define Y second
using namespace std;
typedef pair<int, int> PII;
typedef long long ll;
typedef long double ld;
const int maxn = 1e5+5;
#define int ll
//这个是线段树区间乘和区间加的板子
//核心是维护两个lazy标记,其中一个维护add,一个维护mul
//因为add和mul存在一个先后关系,我们考虑乘法优先就好了
//也就是如果想要add的话就先乘一下mul
struct node{
int l, r;
int sum;
int add;
int mul;
}tr[maxn<<2];
int aa[maxn];
int n, m, p;
void pushup(int u) {tr[u].sum =( tr[u<<1].sum + tr[u<<1|1].sum)%p;}
void build(int u, int l, int r){
if(l==r){
tr[u] = {l, r, aa[l], 0, 1};
}else{
int mid = l+r >> 1;
tr[u] = {l, r, 0, 0, 1};
build(u<<1, l, mid);
build(u<<1|1, mid+1, r);
pushup(u);
}
}
//
void pushdown(int u){
int l = tr[u].l, r = tr[u].r;
int mid = l+r >>1;
//这边要注意不要加上原来的sum了,sum已经被修改了
tr[u<<1].sum = (tr[u<<1].sum*tr[u].mul%p + tr[u].add*(mid-l+1)%p)%p;
tr[u<<1|1].sum = (tr[u<<1|1].sum*tr[u].mul%p + tr[u].add*(r-mid)%p)%p;
//
tr[u<<1].mul = (tr[u<<1].mul*tr[u].mul)%p;
tr[u<<1|1].mul = (tr[u<<1|1].mul*tr[u].mul)%p;
tr[u<<1].add = (tr[u<<1].add*tr[u].mul%p + tr[u].add)%p;
tr[u<<1|1].add = (tr[u<<1|1].add*tr[u].mul%p + tr[u].add)%p;
//
tr[u].mul = 1;
tr[u].add = 0;
}
void update(int u, int l, int r, int mul, int add){
if(l <= tr[u].l && tr[u].r <= r){
tr[u].sum = (tr[u].sum*mul%p + add*(tr[u].r- tr[u].l+1)%p)%p;
tr[u].add = (tr[u].add*mul%p + add%p)%p;
tr[u].mul = (tr[u].mul*mul)%p;
}else{
pushdown(u);
int mid = tr[u].l+tr[u].r >> 1;
if(l<=mid) update(u<<1, l ,r, mul, add);
if(r > mid) update(u<<1|1, l, r, mul, add);
pushup(u);
}
}
int query(int u, int l, int r){
if(l <= tr[u].l && tr[u].r <= r){
return tr[u].sum;
}else{
pushdown(u);
int ret = 0;
int mid = tr[u].l + tr[u].r >>1;
if(l<=mid) ret = (ret%p + query(u<<1, l ,r))%p;
if(r > mid) ret = (ret%p + query(u<<1|1, l, r))%p;
ret %= p;
return ret;
}
}
signed main(){
SF
cin >> n >> m >> p;
for(int i = 1;i <= n;++i) cin >> aa[i];
build(1, 1, n);
while(m--){
int op;cin >> op;
if(op == 1){
int x, y, k;cin >> x >> y >> k;
update(1, x, y, k, 0);
}else if(op == 2){
int x, y, k;cin >> x >> y >> k;
update(1, x, y, 1, k);
}else{
int l, r;cin >> l >> r;
cout << query(1, l, r) << endl;
}
}
return 0;
}
E题Lost Cows
题面
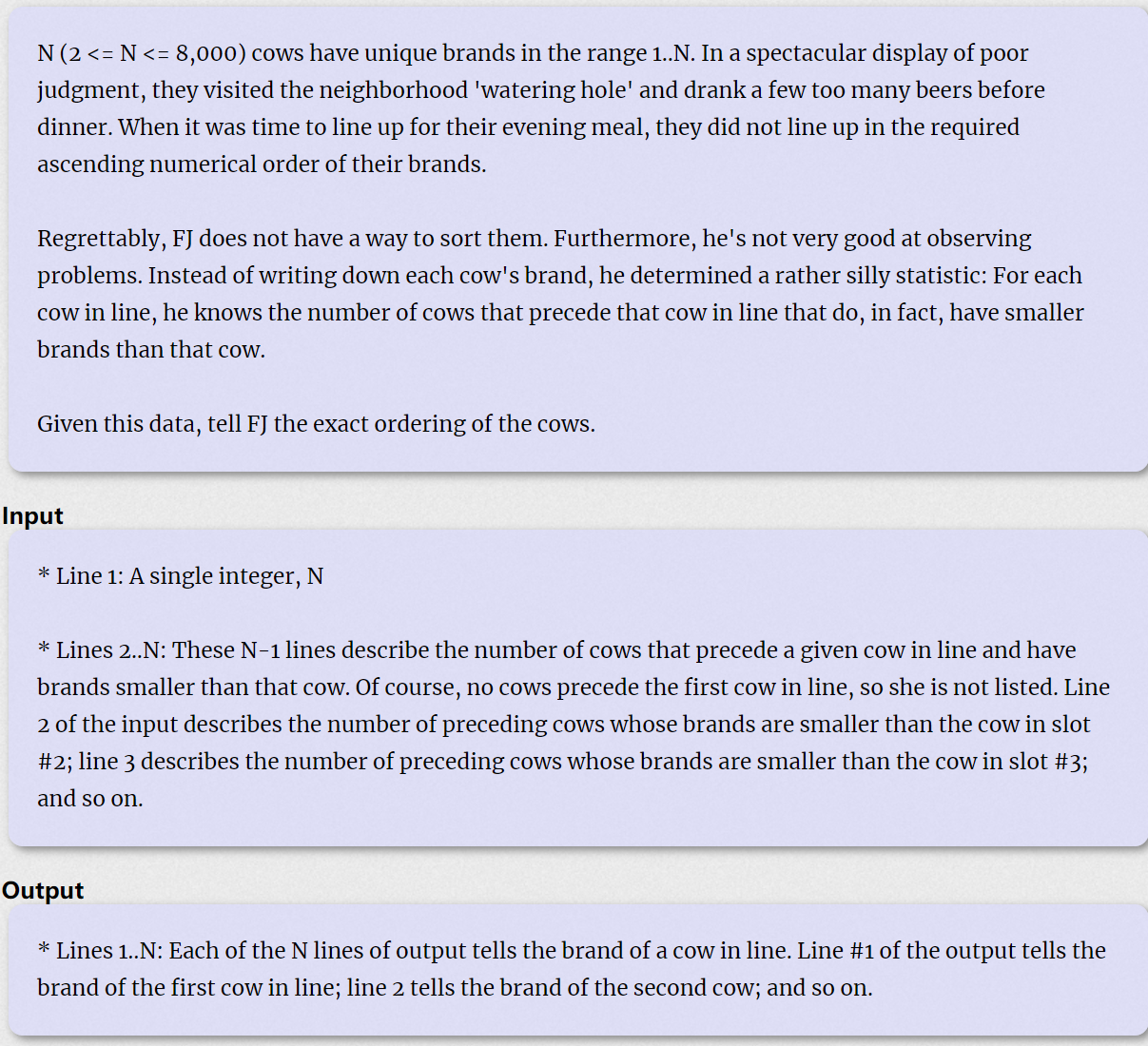
样例

思路
利用树状数组求逆序对,并且利用二分查找优化
代码
#include <iostream>
#include <cstring>
#include <algorithm>
//#pragma comment(linker, "/STACK:102400000,102400000")//手动开大栈区
#define SF ios_base::sync_with_stdio(false);cin.tie(NULL);cout.tie(NULL);
#define ms(x, y) memset(x, y, sizeof(x))
#define INF 0x3f3f3f
#define X first
#define Y second
using namespace std;
typedef pair<int, int> PII;
typedef long long ll;
typedef long double ld;
const int maxn = 8010;
//从后往前求,利用树状数组维护该数在自己之前有几个小于自己的数
int n;
int aa[maxn];
int tr[maxn];
int ret[maxn];
int lowbit(int x){return x& -x;}
void update(int x, int y){
for(int i = x;i <= n;i += lowbit(i)){
tr[i] += y;
}
}
int query(int x){
int sum = 0;
for(int i = x;i;i -= lowbit(i)){
sum += tr[i];
}
return sum;
}
int main(){
SF
cin >> n;
aa[1] = 0;
for(int i = 2;i <= n;++i){
cin >> aa[i];
}
for(int i = 1;i <= n;++i) update(i, 1);
for(int i = n;i >= 1;--i){
int l = 0, r = n, k = aa[i];
while(l < r){
int mid = l+r+1 >> 1;
if(query(mid) > k) r = mid-1;
else l = mid;
}
ret[i] = l+1;
update(l+1, -1);
}
for(int i = 1;i <= n;++i) cout << ret[i] << endl;
return 0;
}
F题Count Color
题面

样例

思路
观察到题目所给的颜色范围只有30个,那就利用二进制串来表示当前每个颜色。然后用线段树
维护当前染了什么颜色就好了
用或操作可以很好的维护颜色的加法
代码
#include <iostream>
#include <algorithm>
//#pragma comment(linker, "/STACK:102400000,102400000")//手动开大栈区
#define SF ios_base::sync_with_stdio(false);cin.tie(NULL);cout.tie(NULL);
#define ms(x, y) memset(x, y, sizeof(x))
#define INF 0x3f3f3f
#define X first
#define Y second
using namespace std;
typedef pair<int, int> PII;
typedef long long ll;
typedef long double ld;
const int maxn = 1e5+10;
//这里是用二进制串来表示颜色
struct node {
int l, r;
int num;
int lazy;
}tr[maxn<<2];
int color[50];
void init(){
color[1] = 1;
int cnt = 30;
int pos = 2;
while(pos <= cnt){
color[pos] = color[pos-1]*2;
pos++;
}
}
//父节点等于两个子节点拥有的颜色相加
void pushup(int u) {tr[u].num = (tr[u<<1].num | tr[u<<1|1].num);}
void build(int u, int l, int r){
if(l == r){
tr[u] = {l, r, 1, 0};
}else{
tr[u] = {l, r, 1, 0};
int mid = l+r >> 1;
build(u<<1, l , mid);
build(u<<1|1, mid+1, r);
}
}
//涂色
void pushdown(int u){
if(tr[u].lazy == 0) return;
tr[u<<1].num = tr[u].lazy;
tr[u<<1|1].num = tr[u].lazy;
//
tr[u<<1].lazy = tr[u].lazy;
tr[u<<1|1].lazy = tr[u].lazy;
//
tr[u].lazy = 0;
}
void update(int u, int l, int r, int d){
if(l <= tr[u].l && tr[u].r <= r){
tr[u].num = color[d];
tr[u].lazy = color[d];
}else{
pushdown(u);
int mid = tr[u].l+tr[u].r >> 1;
if(mid >= l) update(u<<1, l, r, d);
if(mid < r) update(u<<1|1, l, r, d);
pushup(u);
}
}
int query(int u, int l, int r){
if(l <= tr[u].l && tr[u].r <= r){
return tr[u].num;
}else{
int ans = 0;
pushdown(u);
int mid = tr[u].l+tr[u].r >> 1;
if(mid >= l) ans |= query(u<<1, l, r);
if(mid < r) ans |= query(u<<1|1, l, r);
return ans;
}
}
int main(){
SF
init();
int L , T, O;cin >> L >> T >> O;
build(1, 1, L);
while(O--){
char op;cin >> op;
if(op == 'C'){
int l, r, d;cin >> l >> r >> d;
if(l > r) swap(l, r);
update(1, l ,r, d);
}else if(op == 'P'){
int l, r;cin >> l >> r;
if(l > r) swap(l, r);
int q = query(1, l, r);
int cnt = 0;
//数有多少个颜色就好了
while(q){
if(q&1) cnt++;
q >>= 1;
}
cout << cnt << endl;
}
}
return 0;
}
G题Mayor's posters
题面


样例
题意
现在有一块板,大家往上面贴海报,海报占地区间是L,R,问你贴到最后有几张海报可见。
思路
线段树维护当前区间被什么颜色占领,有趣的点在于你当前区间的两个子区间不是同一个海报的话显然没办法合并,必须要继续往下查询。
然后发现会MLE。
于是观察到最多只可能有1e4对LR,也就是实际上最多只有2e4个点,将数据离散化一下就能缩小线段树的范围
代码
#include <iostream>
#include <algorithm>
#include <cstring>
#include <vector>
//#pragma comment(linker, "/STACK:102400000,102400000")//手动开大栈区
#define SF ios_base::sync_with_stdio(false);cin.tie(NULL);cout.tie(NULL);
#define ms(x, y) memset(x, y, sizeof(x))
#define INF 0x3f3f3f
#define X first
#define Y second
using namespace std;
typedef pair<int, int> PII;
typedef long long ll;
typedef long double ld;
const int maxn = 2e5+10;
//这题是将数据离散化,如果直接开大数组的话会MLE的
int ans = 0;
int tr[maxn<<2];
bool vis[maxn];
vector<PII > dui;
vector<int> lisan;
void pushup(int u){
if(tr[u<<1] != tr[u<<1|1]) tr[u] = 0;
else tr[u] = tr[u<<1];
}
void build(int u , int l, int r){
if(l == r){
tr[u] = 0;
return;
}
int mid = l + r >>1;
build(u<<1, l, mid);
build(u<<1|1, mid+1, r);
}
void pushdown(int u){
tr[u<<1] = tr[u];
tr[u<<1|1] = tr[u];
}
void update(int u, int L, int R, int l, int r, int d){
if(L <= l && r <= R){
tr[u] = d;
}else{
if(l == r) return;
if(tr[u] != 0) pushdown(u);
int mid = l+r>>1;
if(mid >= L) update(u<<1, L, R, l, mid, d);
if(mid < R) update(u<<1|1, L, R, mid+1, r, d);
pushup(u);
}
}
void query(int u, int L, int R, int l, int r){
if(L <= l && r <= R && tr[u]){
vis[tr[u]] = 1;
}else{
if(l == r) return;
if(tr[u] != 0) pushdown(u);
int mid = l+r>>1;
if(mid >= L) query(u<<1, L, R, l , mid);
if(mid < R) query(u<<1|1, L, R, mid+1, r);
}
}
int main(){
SF
int t;cin >> t;
while(t--){
dui.clear();
lisan.clear();
int x;cin >> x;
int cnt = 0;
for(int i = 1;i <= x;++i) {
int l, r;cin >> l >> r;
dui.push_back({l, r});
lisan.push_back(l);
lisan.push_back(r);
}
sort(lisan.begin(), lisan.end());
lisan.erase(unique(lisan.begin(), lisan.end()), lisan.end());
int len = lisan.size();
build(1, 1, len);
for(int i = 0;i < x;++i){
int l = dui[i].X, r = dui[i].Y;
l = lower_bound(lisan.begin(), lisan.end(), l)-lisan.begin()+1;
r = lower_bound(lisan.begin(), lisan.end(), r)-lisan.begin()+1;
update(1, l, r, 1, len, i+1);
}
query(1, 1, len, 1, len);
for(int i = 1;i <= x;++i){
if(vis[i]) cnt++, vis[i] = 0;
}
cout << cnt << endl;
}
return 0;
}
后话
树状数组和线段树这俩东西的话一开始学起来会比较困难,但是打的题多了感觉还是大差不差的。



