2022GDUT寒训专题四
C题 Beautiful Numbers
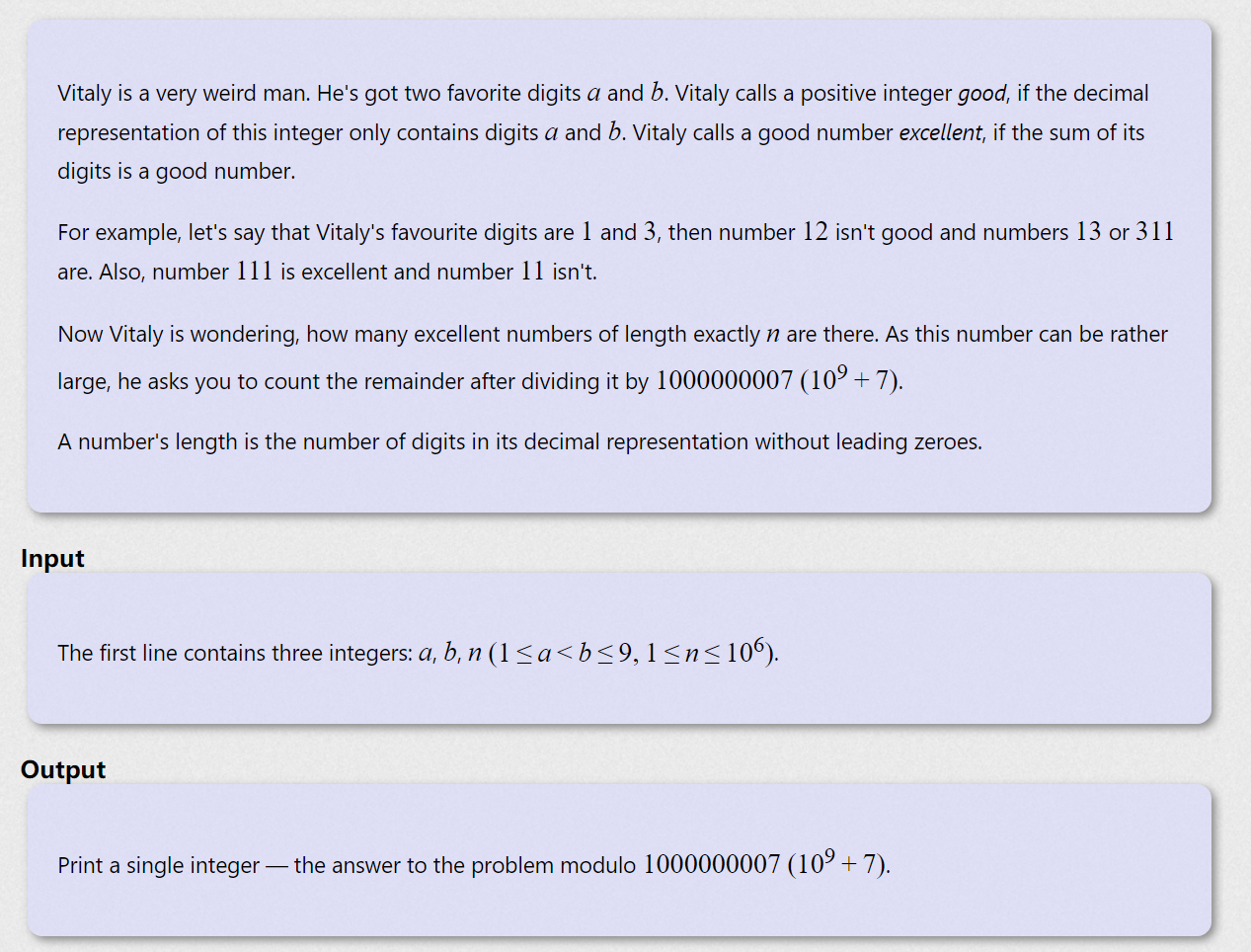
题面
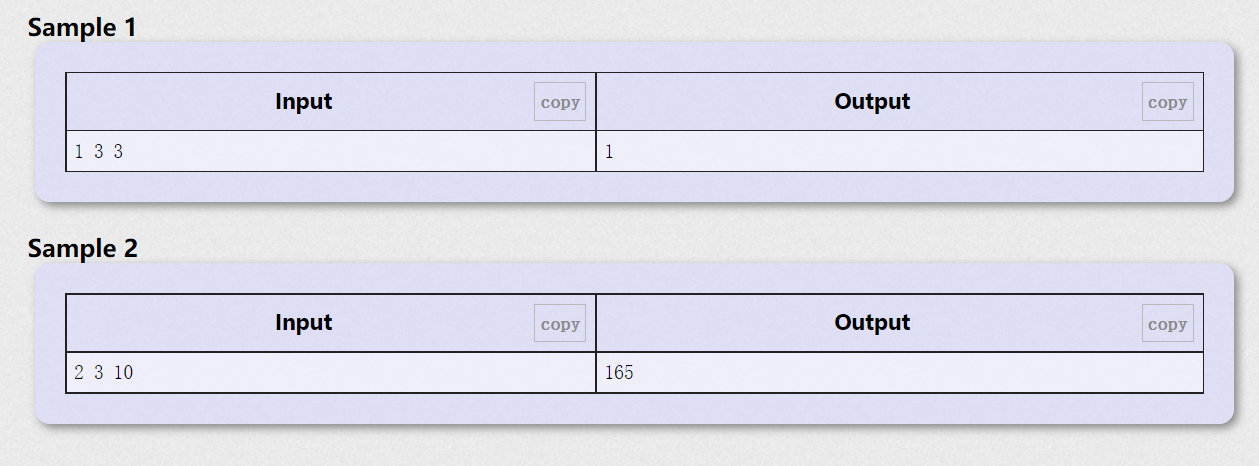
样例
题意
意思是问你给定数字a, b和所想要生成数字的位数n,问你在这样的条件下有多少个数满足每一位相加之后也只由数字a, b构成
思路
因为我们知道n的长度是1e6,也就是估摸着求和不会超过1e7,所以求和出来的数的位数应该最多只有7位数,直接一个暴力枚举+组合数就好了
也就是枚举在长度n限制下有多少个a,有多少个b就好了
然后这个地方要预处理一下组合数,也要运用到逆元
代码
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
typedef long double ld;
typedef pair<int, int> PII;
const int inf = 0x3f3f3f;
const ll p = 1e9+7;
const int maxn = 1e6+10;
ll a, b, n;
ll f[maxn];
void pre(){
f[0] = 1;
f[1] = 1;
for(int i = 2;i <= 1000000;++i){
f[i] = f[i-1]*i%p;
}
}
ll fp(ll base, ll power){
ll ret = 1;
while(power > 0){
if(power&1){
ret = ret*base%p;
}
base = base*base%p;
power >>= 1;
}
return ret;
}
bool check(ll a, ll b, ll x){
while(x){
ll temp = x % 10;
if((temp != a) && (temp != b)) return false;
x /= 10;
}
return true;
}
int main(){
ios_base::sync_with_stdio(false);
cin.tie(NULL);cout.tie(NULL);
//
pre();
cin >> a >> b >> n;
ll ans = 0;
for(int i = 0;i <= n;++i){
ll t = a*i + b*(n-i);
if(check(a, b, t)){
ll down = f[n-i]*f[i]%p;
ll tot = f[n]*fp(down, p-2)%p;
ans = ans%p + tot%p;
ans %= p;
}
}
cout << ans %p << endl;
return 0;
}
// printf("**********test**********\n");
// printf("%d\n");
// printf("**********test**********\n");
E题 Prime Distance
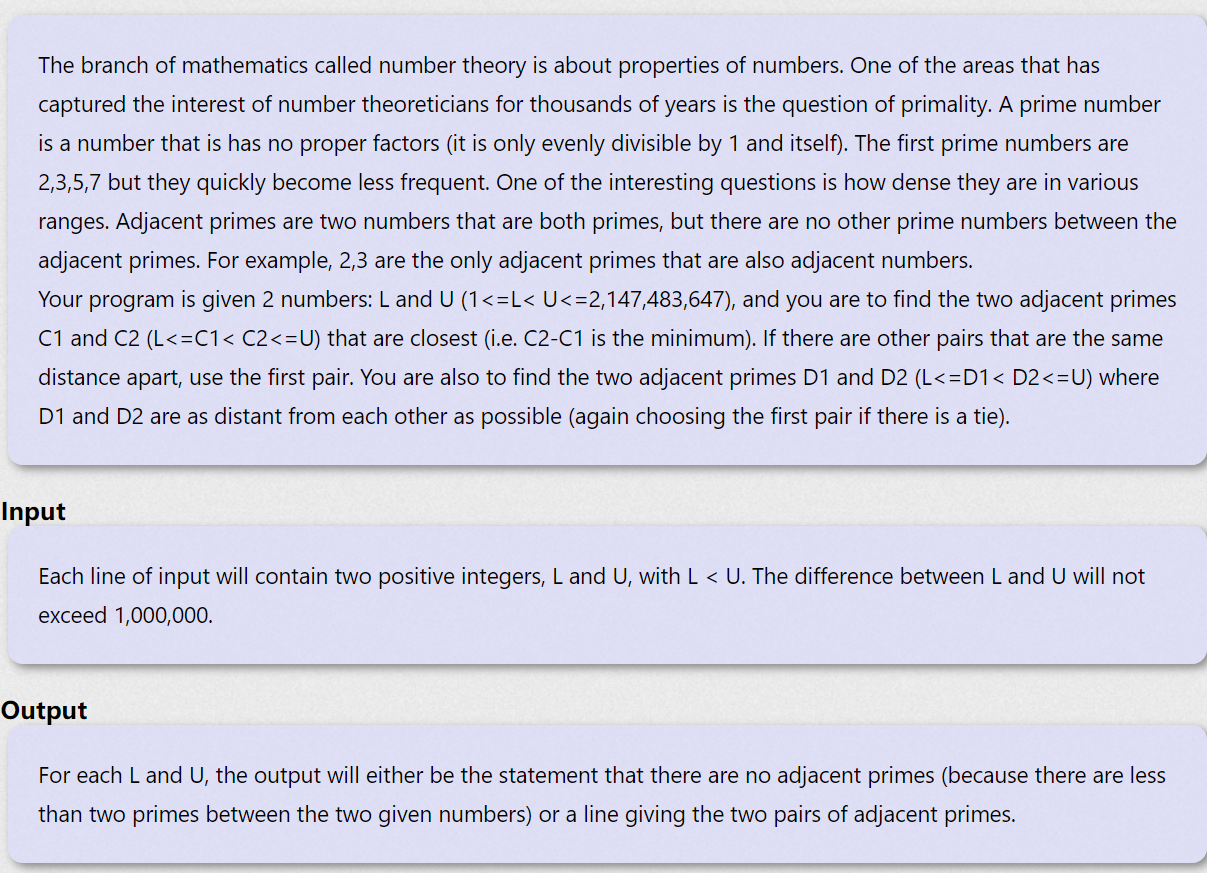
题面
样例

题意
给定l, r区间,问你距离最近的素数对以及距离最远的素数对
如果有多对答案相同的话,输出从左往右找到的第一位
思路
这题给的l,r范围很大,区间长度却很小,考虑区间筛质数
显然直接使用埃筛是存不下这么大的数的
所以我们考虑使用两次埃筛,第一次预处理筛出这个大范围内可能可以成为因子的素数,也就是sqrt(_max),其中_max为题目所给范围。
第二次筛我们就根据所给的l r区间来筛,给lr区间加一个偏移量就可以存下了
然后筛掉区间内的合数,剩下的数就是区间内的素数咯
代码
#include <iostream>
#include <cstdio>
#include <vector>
#include <cstring>
#include <algorithm>
using namespace std;
typedef long long ll;
typedef long double ld;
typedef pair<int, int> PII;
const int inf = 0x3f3f3f;
//这个是区间筛素数的典例
//主要还是用埃筛的思想吧
//还有主要是看到这个l, r之差只有1e6,所以对数组下标加一个偏移量就可以存下咯
//不过写的时候确实还有很多细节要注意啦...
ll l, r;
ll first_l, first_r, second_l, second_r;
bool x[50010];
bool y[6000010];
vector<int>prime;
vector<ll>ans;
//先得到5e4以内的素数
void Smallprime(){
memset(x, 1, sizeof(x));
x[1] = 0;
x[2] = 1;
for(ll i = 2;i <= 50000;++i){
if(x[i]){
prime.push_back(i);
for(ll j = 2;i*j <= 50000;++j){
x[i*j] = 0;
}
}
}
}
//然后用5e4的素数来筛更大区间的合数
//因为区间长度不超过1e6,所以检验数组加一个偏移量就好啦,就是让l作为0就好咯
void Bigprime(){
memset(y, 1, sizeof(y));
for(ll i = 0;i < prime.size();++i){
//要先处理一下倍数...不然单纯暴力会t的
//距离l最近是prime的几倍
ll a = (l-1)/prime[i]+1;
ll b = r/prime[i];
for(ll j = a;j <= b;++j){
if(j > 1) y[j*prime[i]-l] = 0;
}
}
}
//检验当前点是否为素数,是的话压入答案容器里
void _push(){
for(ll i = 0;i <= r-l;++i){
if(y[i-l]) ans.push_back(i);
}
}
//遍历ans容器,找到答案
bool check(){
//起码要有两个素数才有答案噢
if(ans.size() <= 1) return false;
//for(auto x:ans){cout << x << endl;}
ll _min = inf, _max = -1;
ll len = 0;
for(ll i = 1;i < ans.size();++i){
len = ans[i]-ans[i-1];
if(len > _max){
_max = len;
second_l = ans[i-1];
second_r = ans[i];
}
if(len < _min){
_min = len;
first_l = ans[i-1];
first_r = ans[i];
}
}
return true;
}
int main(){
ios_base::sync_with_stdio(false);
cin.tie(NULL);cout.tie(NULL);
//
Smallprime();
while(~scanf("%lld%lld", &l, &r)){
//这个地方要特判一下1,不然会wa
if(l == 1) l = 2;
ans.clear();
Bigprime();
_push();
if(!check()) printf("There are no adjacent primes.\n");
else {
printf("%lld,%lld are closest, %lld,%lld are most distant.\n", first_l, first_r, second_l, second_r);
}
}
return 0;
}
// printf("**********test**********\n");
// printf("%d\n");
// printf("**********test**********\n");
G题 青蛙的约会
题面

样例

思路
先记二者为A和B。设跳的次数为t,走的总路程为p,因为是转圈,所以得到A走的路程和B走的路程对L同余即可,对方程进行变形,发现变量只有t和p,也就是求解这个不定方程。利用拓展欧几里得算法就可以求得答案
因为拓展欧几里得算法所求得的整数解不一定是最小正整数解,所以利用其通解形式可以得到最小正整数解
代码
#include <iostream>
#include <cstdio>
#include <algorithm>
#include <cstring>
using namespace std;
typedef long long ll;
typedef long double ld;
typedef pair<int, int> PII;
const int inf = 0x3f3f3f;
ll x, y, m, n, l, t, p;
ll gcd(ll a, ll b) {if(b == 0) return a;else return gcd(b, a%b);}
ll exgcd(ll a, ll b, ll &x, ll&y){
if(b == 0){
x = 1;
y = 0;
return a;
}
ll g = exgcd(b, a%b, x, y);
ll temp = x;
x = y;
y = temp - y*(a/b);
return g;
}
ll want(ll x0, ll y0){
return (x0%y0+y0)%y0;
}
int main(){
ios_base::sync_with_stdio(false);
cin.tie(NULL);cout.tie(NULL);
//
cin >> x >> y >> m >> n >> l;
int a1 = n-m, b1 = l, c1 = x-y;
if(a1 < 0) {a1 = -a1;c1 = -c1;}
ll k = gcd(a1, b1);
if(c1 % k) puts("Impossible");
else{
exgcd(a1, b1, t, p);
//x的通解x_0 + k*u, u = b/gcd(a, b),所以求最小解就mod这个就好咯
//y的通解y_0 - k*u, u = a/gcd(a, b)
ll mod = b1/k;
//因为刚刚求的是右边是gcd(a,b)即这里说的k的情况,所以要还原为原本的解噢
cout << want(t*c1/k, mod) << "\n";
}
return 0;
}
// printf("**********test**********\n");
// printf("%d\n");
// printf("**********test**********\n");
后话
对于拓展欧几里得算法,只需要记住一点,我们默认传入exgcd所解方程的右侧为gcd(a, b),那么得到的解不一定是原题所要求的解,我们需要乘上一定的系数才是原题所求的答案。
J题 Cheerleaders
题面

样例

题意
给定n x m的棋盘和k个人,现在要求每条边上一定都得有人站着,问你满足条件的情况数
思路
思路很好想到,就是利用容斥原理
但是这个地方很有意思的点是我第一次遇到状态压缩,感觉是一个很有用的小技巧
代码
#include <bits/stdc++.h>
#define SF ios_base::sync_with_stdio(false);cin.tie(NULL);cout.tie(NULL);
#define ms(x, y) memset(x, y, sizeof(x))
#define INF 0x3f3f3f
#define X first
#define Y second
using namespace std;
typedef pair<int, int> PII;
typedef long long ll;
typedef long double ld;
const int p = 1e6+7;
const int maxn = 410;
//这题是容斥原理+状态压缩,还是挺有意思的qvq
ll f[maxn][maxn];
//因为数据范围很小,所以预处理组合数的话直接上状态转移就好咯
void cal(){
for(int i = 0;i <= 400;++i){
f[i][0] = f[i][i] = 1;
}
for(int i = 0;i <= 400;++i){
for(int j = 0;j < i;++j){
f[i][j] = (f[i-1][j] + f[i-1][j-1]) % p;
}
}
}
int main(){
SF
cal();
int t;cin >> t;
int cnt = 0;
while(t--){
int m, n, k;cin >> m >> n >> k;
ll ans = 0;
//这个地方很有趣欸,是状态压缩!
//对于四条边,都只有两种状态:有或者没有人
//所以我们用四位的01串来分别表示上下左右有没有人
for(int i = 0; i < 16;++i){
int cnt = 0, r = n, c = m;
if(i&1) {cnt++;c--;}
if(i&2) {cnt++;c--;}
if(i&4) {cnt++;r--;}
if(i&8) {cnt++;r--;}
//对于容斥原理来说,过程是奇减偶加,所以统计有奇数条边就是减,反之为加
if(cnt&1) ans = (ans%p + p - f[r*c][k]%p) % p;
else ans = (ans%p + f[r*c][k]%p) % p;
}
printf("Case %d: %lld\n", ++cnt, ans);
}
return 0;
}
// printf("**********test**********\n");
// printf("%d\n");
// printf("**********test**********\n");
后话
容斥原理是奇减偶加的
总结
数论专题的话,反而是接触的稍微多一点,感觉主要是组合数学+素数+拓展欧几里得用的比较多一些
还有快速幂求逆元也是非常常用的地方,毕竟一般给的模数都是质数,不过如果模数不是质数的话利用exgcd也可以
还有欧拉函数也是稍微会用到一点,也就是会用到性质吧(L题)。不过这里没给出来,因为我利用欧拉函数的解法写起来会稍微复杂一点,不如直接用gcd直接求哈哈哈。



 浙公网安备 33010602011771号
浙公网安备 33010602011771号