2022GDUT寒训专题三
C题 The Suspects
题面

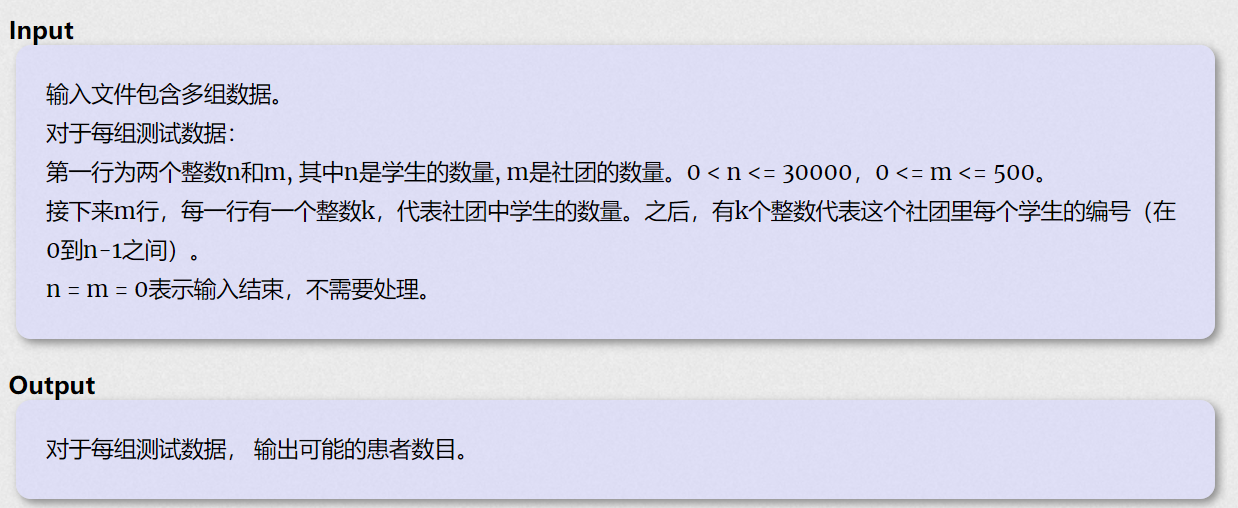
补充说明:0为患者,输出0所在的连通块的大小
思路
这题就是并查集的板子题,有意思的点是维护连通块核心所连接的成员的数量,在计算总数量的时候实际上是核心所记录数量的转移
代码
#include <iostream>
#include <algorithm>
#include <vector>
using namespace std;
typedef long long ll;
typedef long double ld;
typedef pair<int, int> PII;
const int inf = 0x3f3f3f;
const int maxn = 3e4+10;
//并查集板子题,这题的特色是找连通块的大小
//只需要多开一个数组,维护核心的cnt就行了,就是在merge里加一行
int father[maxn];
int cnt[maxn];
void init(int len)
{
for(int i = 0;i < len;++i)
{
father[i] = i;
cnt[i] = 1;
}
}
int get(int x)
{
if(father[x] == x) return x;
else return father[x] = get(father[x]);
}
void merge(int x, int y)
{
x = get(x);
y = get(y);
if(x != y)
{
father[y] = x;
//核心大小的转移
cnt[x] += cnt[y];
}
}
int main()
{
ios_base::sync_with_stdio(false);
cin.tie(NULL);cout.tie(NULL);
//
int n, m;
while(cin >> n >> m)
{
if(n == 0 && m == 0) break;
//
init(n);
while(m--)
{
int k;cin >> k;
if(k == 0) continue;
vector<int>record(k);
for(int i = 0;i < k;++i) cin >> record[i];
if(k >= 2)
{
for(int i = 1;i < record.size();++i)
{
merge(record[i], record[i-1]);
}
}
}
int ans = get(0);
ans = cnt[ans];
cout << ans << endl;
}
return 0;
}
后话
关于并查集的应用,本质上是维护核心,一般来讲我们都用带路径压缩的get()。
板子
//带路径压缩
int get (int x)
{
if(father[x] == x) return x;
else return father[x] = get(father[x]);
}
//连接二者的父节点,默认连到左节点上
void merge(int x, int y)
{
x = get(x);
y = get(y);
if(x != y) father[y] = x;
}
F题 Built?
题面
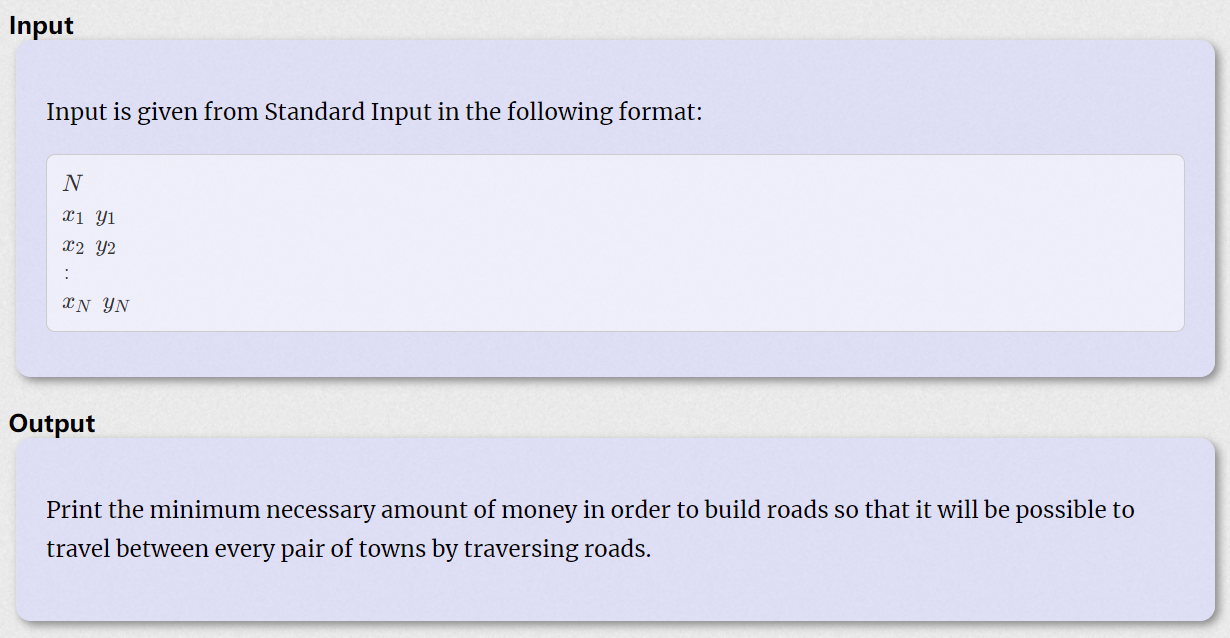
样例
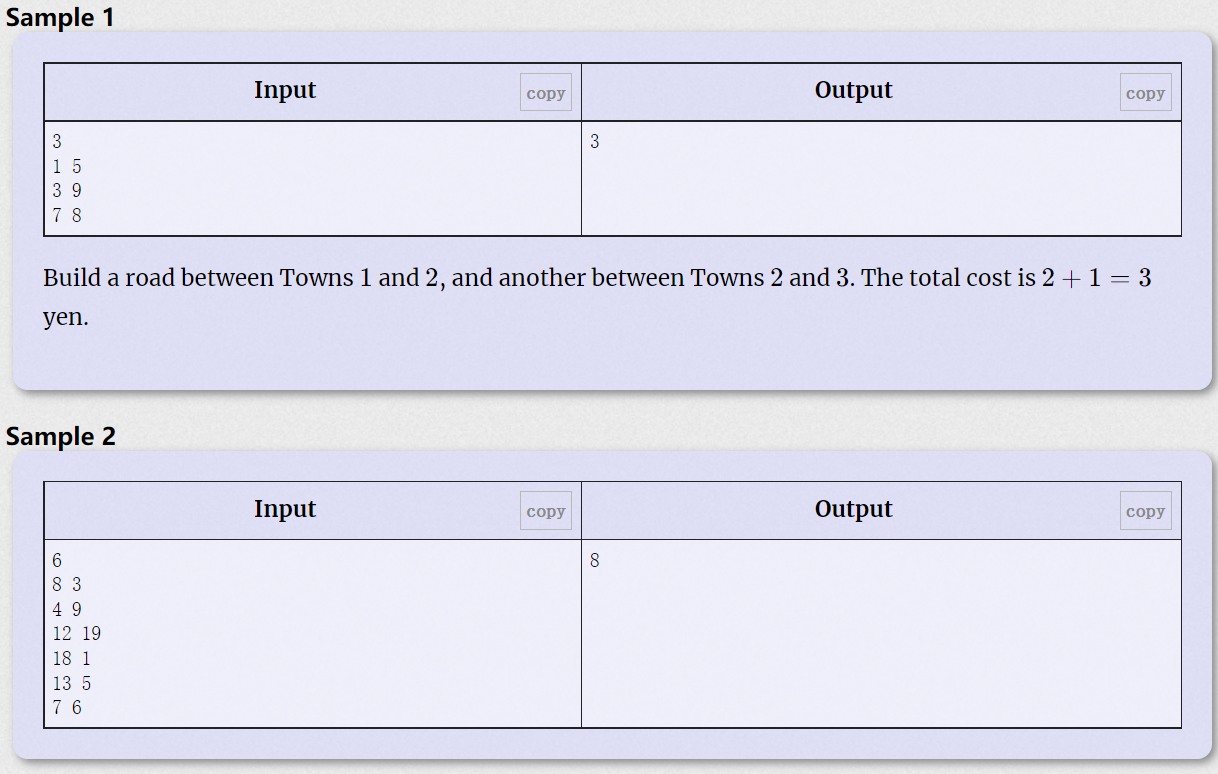
题意
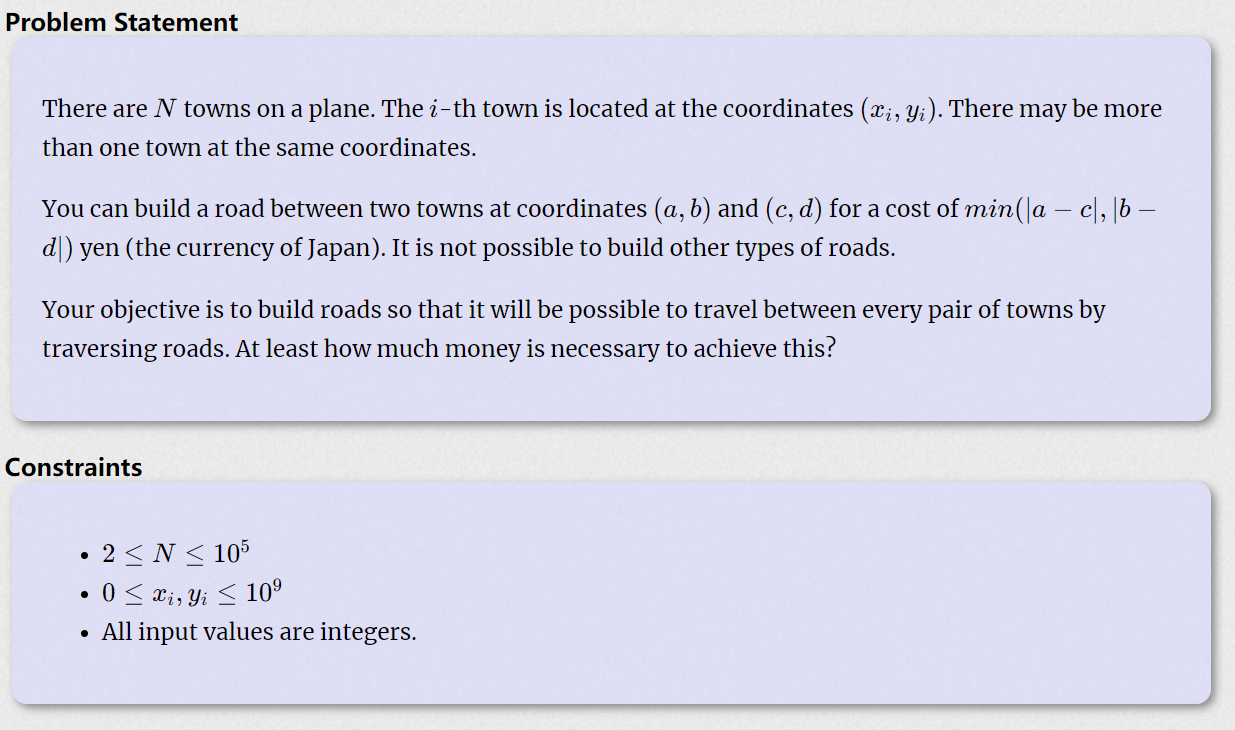
这题大意是说给定N个点,这N个点之间距离规定为两点横坐标之差与纵坐标之差取min,问你现在最少需要多长的路径才可以将这些点连通。
思路
这题主要是贪心+kruskal算法。
因为我们知道边的权值一定是两点横坐标之差与纵坐标之差取min,所以我们先假设这样一种情景:将所有点的横坐标与纵坐标只差压入同一个新容器中后按升序排序,两点之间的真正的那个边权一定会在要舍弃的那个边权之前。
这时候我们处理边还是O(\(n^2\))的,但是我们可以继续优化,由贪心我们只需要存最短的边即可。所以我们先把x坐标、y坐标分别装在容器xx与容器yy中。然后对容器xx和容器yy升序排序,那么得到的xx或者是yy容器中的序列的相邻的两点一定是差最小的,也就是边权最短的。
处理完xx,yy之后可以分别得到n-1条边,然后将这2n-2条边压入同一个容器后再按升序排序,使用kruskal算法得到最小生成树即可得到答案
代码
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
typedef long double ld;
typedef pair<int, int> PII;
const int inf = 0x3f3f3f;
const int maxn = 1e5+10;
//这题是贪心+kruskal+并查集
//因为要求城市之间的路径最短,又因为知道是横坐标只差或者是纵坐标只差
//所以我们备份两个数组,分别按照横坐标和纵坐标排序,这样得到的两个点的坐标差在一个维度上一定是最小的
//然后将这两组数组得到的边全部压入一个新的容器里,对这个新的容器使用kruskal算法即可
struct node{
int a, b, c;
};
struct fi{
int u, v, w;
};
int N;
int father[maxn];
vector<struct node> xx;
vector<struct node> yy;
vector<struct fi> ee;
bool cmpx(struct node x, struct node y){return x.a < y.a;}
bool cmpy(struct node x, struct node y){return x.b < y.b;}
bool cmpw(struct fi x, struct fi y){return x.w < y.w;}
int get(int x){
if (father[x] == x) return x;
else return father[x] = get(father[x]);
}
int main()
{
ios_base::sync_with_stdio(false);
cin.tie(NULL);cout.tie(NULL);
//
cin >> N;
for(int i = 0;i < N;++i) father[i] = i;
for(int i = 0;i < N;++i){
int x, y;cin >> x >> y;
xx.push_back({x, y, i});
yy.push_back({x, y, i});
}
sort(xx.begin(), xx.end(), cmpx);
sort(yy.begin(), yy.end(), cmpy);
for(int i = 1;i < xx.size();++i){
ee.push_back({xx[i-1].c, xx[i].c, (xx[i].a-xx[i-1].a)});
}
for(int i = 1;i < yy.size();++i){
ee.push_back({yy[i-1].c, yy[i].c, (yy[i].b-yy[i-1].b)});
}
sort(ee.begin(), ee.end(), cmpw);
int ans = 0;
int cnt = 0;
//kruskal算法的话一定要用并查集来判断是否连通,因为如果单纯用vis来标记的话会漏边的
for(int i = 0;i < ee.size();++i){
int a = ee[i].u, b = ee[i].v, w = ee[i].w;
a = get(a);
b = get(b);
if(a != b)
{
father[b] = a;
ans += w;
cnt++;
}
if(cnt == N-1) break;
}
cout << ans << endl;
return 0;
}
后话
使用kruskal算法来得到最小生成树的话,所花费的时间是O(\(mlogm\))的。本质上也是一种贪心的算法。简要介绍就是将所有当前的边按边权升序排序,将每一条边依次加入到连通块上即可。
也可以用来检验图是否连通,如果n个点连通的话最少需要n-1条边,如果达不到n-1条边的话就说明不连通。
板子
int kruskal()
{
sort(edges, edges + m);
for (int i = 1; i <= n; i ++ ) p[i] = i; // 初始化并查集
int res = 0, cnt = 0;
for (int i = 0; i < m; i ++ )
{
int a = edges[i].a, b = edges[i].b, w = edges[i].w;
a = find(a), b = find(b);
if (a != b)
{
p[a] = b;
res += w;
cnt ++ ;
}
}
if (cnt < n - 1) return INF;
return res;
}
I题 Drazil and Tiles
题面


样例

题意
给定\(n*m\)大小的棋盘,其中''代表已经为满,'.'代表为空,你现在有无限个\(1*2\) 大小的小瓦片,问你是否有可以填满棋盘的唯一解,有的话输出唯一解,否则输出"Not unique"(这里包括有解但不唯一)。
思路
这题要用到拓扑排序以及bfs的思想。首先我们规定一个点可以有上下左右四种方向的边,并且我们在这里称为出度(这里只对'.'的点进行讨论)。
我们先思考什么情况下有唯一解:也就是说每一个位置下的小瓦片只可以有一种摆法。那么我们每一步总是可以找到起码一个点,他的出度为1。
粗略证明:
反证法:假设我们现在在棋盘上连任意一个出度为1的点都找不到,那么可能是两种情况:
1、任意一点的出度为0:这样的话没有办法放下1x2的小瓦片,是无解。
2、任意一点的出度大于等于2,这样的话我们可以用类似汉诺塔的思想,知道总是存在可以将当前解转换为另外一种形式解的情况,解不唯一。
由此如果存在填满棋盘的唯一解,那么一定是存在出度为1的点。
然后使用bfs的思路,这个点处理完后就拓展他四周的点,将满足条件的点加入队列中等待下一轮的处理。
最后我们只需要遍历一遍棋盘,看看是否完全被填满即可。
(感觉说的有点乱,只可意会不可言传哈哈哈哈哈哈)
代码
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
typedef long double ld;
typedef pair<int, int> PII;
const int inf = 0x3f3f3f;
//这道题像是top排序的变种问题
//我们首先知道一点,就是如果存在唯一解的话,那走的每一步都是唯一的,也就是说出度为一
//然后每次找到出度为一的点加入队列中即可
const int maxn = 2010;
struct node{
int a, b;
};
int n, m;
char g[maxn][maxn];
deque<struct node> q;
int num[4][2] = {{1, 0}, {0, 1}, {-1, 0}, {0, -1}};
bool check(int x, int y){
int cnt = 0;
if(g[x+1][y] == '.' && g[x][y] == '.') cnt++;
if(g[x][y+1] == '.' && g[x][y] == '.') cnt++;
if(x-1 > 0) if(g[x-1][y] == '.' && g[x][y] == '.') cnt++;
if(y-1 > 0) if(g[x][y-1] == '.' && g[x][y] == '.') cnt++;
if(cnt == 1) return true;
else return false;
}
struct node add(int x, int y){
struct node ans;
if(g[x+1][y] == '.' && g[x][y] == '.'){
g[x][y] = '^';
g[x+1][y] = 'v';
ans.a = x+1;
ans.b = y;
}
else if(g[x][y+1] == '.' && g[x][y] == '.'){
g[x][y+1] = '>';
g[x][y] = '<';
ans.a = x;
ans.b = y+1;
}
else if(g[x-1][y] == '.' && g[x][y] == '.'){
g[x-1][y] = '^';
g[x][y] = 'v';
ans.a = x-1;
ans.b = y;
}
else if(g[x][y-1] == '.' && g[x][y] == '.'){
g[x][y] = '>';
g[x][y-1] = '<';
ans.a = x;
ans.b = y-1;
}
return ans;
}
void topsort(){
for(int i = 1;i <= n;++i){
for(int j = 1;j <= m;++j){
if(check(i, j)){
struct node temp = add(i, j);
for(int i = 0;i < 4;++i){
int tx = temp.a+num[i][0];
int ty = temp.b+num[i][1];
if(check(tx, ty)) q.push_back({tx, ty});
}
}
}
}
//
while(!q.empty()){
int tx = q.front().a;
int ty = q.front().b;
q.pop_front();
if(check(tx, ty)) {
struct node temp = add(tx, ty);
for(int i = 0;i < 4;++i){
int ta = temp.a+num[i][0];
int tb = temp.b+num[i][1];
if(check(ta, tb)) q.push_back({ta, tb});
}
}
}
}
bool f(){
for(int i = 1;i <= n;++i){
for(int j = 1;j <= m;++j){
if(g[i][j] == '.') return false;
}
}
return true;
}
int main(){
ios_base::sync_with_stdio(false);
cin.tie(NULL);cout.tie(NULL);
//
cin >> n >> m;
for(int i = 1;i <= n;++i)
for(int j = 1;j <= m;++j)
cin >> g[i][j];
topsort();
if(f()){
for(int i = 1;i <= n;++i){
for(int j = 1;j <= m;++j){
cout << g[i][j];
}
cout << endl;
}
}else{
cout << "Not unique" << endl;
}
return 0;
}
后话
这题确实是有意思,没想到拓扑排序还能这么用。
简单介绍一下拓扑排序:
总是找到入度为0的点,将其加入队列中,每个点只加入一次,然后枚举更新这个点的出边,将这些出边所对应点的入度都减1,然后再次将入度为0的点加入队列中。这样得到的序列称为拓扑序列。如果n个点存在这样的拓扑序列,那么一定是加入了n-1条边的。
若想要得到拓扑序列只需要一直将队头压入一个新容器中即可。
还有感觉top排序用邻接表存储的话会稍微好用一些,毕竟是枚举出边嘛。
板子
这板子其实是专题的H题
#include <cstring>
#include <algorithm>
#include <vector>
#include <deque>
using namespace std;
typedef long long ll;
typedef long double ld;
typedef pair<int, int> PII;
const int inf = 0x3f3f3f;
const int maxn = 110;
//top排序板子题,如果要记录下来top排序的序列的话就是拿一个vector接队列头元素就好了
int n;
vector<int> g[maxn];
int in[maxn];
int out[maxn];
vector<int> ans;
deque<int> q;
void topsort()
{
for(int i = 1;i <= n;++i){
if(!in[i]) q.push_back(i);
}
while(!q.empty()){
int t = q.front();
ans.push_back(t);
q.pop_front();
for(int i = 0; i < g[t].size();++i){
int index = g[t][i];
in[index]--;
if(in[index] == 0){
q.push_back(index);
}
}
}
}
int main()
{
ios_base::sync_with_stdio(false);
cin.tie(NULL);cout.tie(NULL);
//
cin >> n;
//
for(int i = 1;i <= n;++i){
int x;
while(cin >> x){
if(x == 0) break;
g[i].push_back(x);
in[x]++;
out[i]++;
}
}
topsort();
for(int i = 0;i < ans.size();++i) cout << ans[i] << " ";
cout << endl;
return 0;
}
L题 Cow Contest
题面
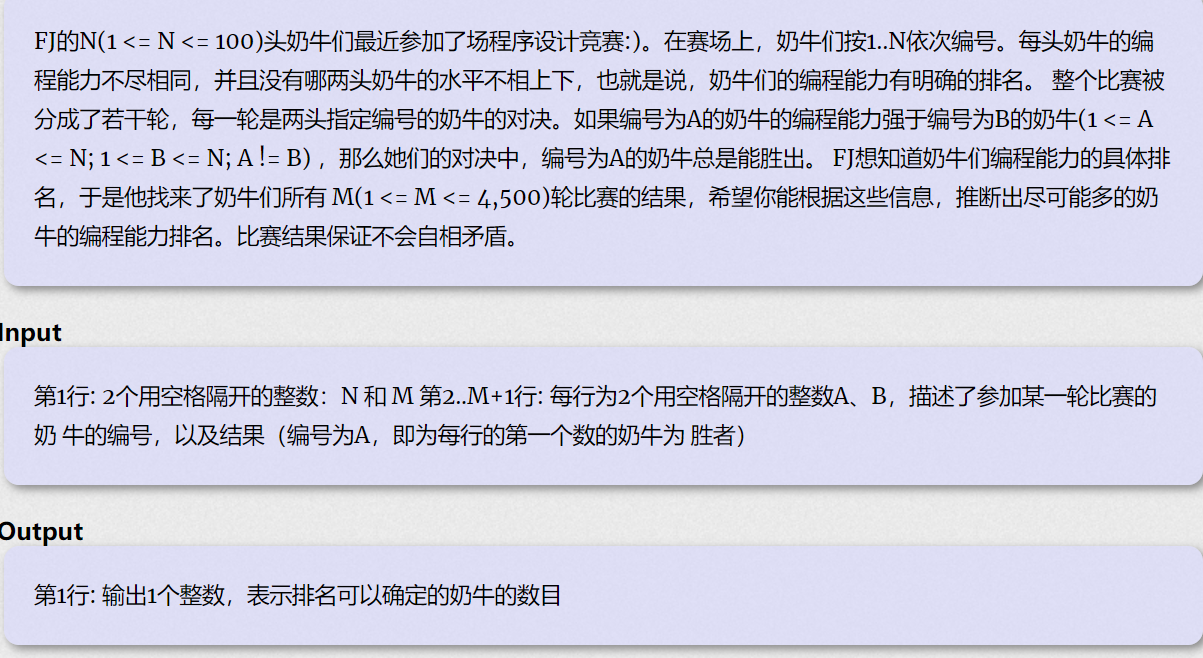
样例

思路
如果一个奶牛的排名能确定,就是说他知道自己在所有奶牛中的相对位置,也就是说他到图上所有的点都连通。
然后我们使用Floyd算法就可以得到一张连通图,判断这只奶牛是否到所有的点都连通即可,若是的话ans++。
代码
#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
typedef long long ll;
typedef long double ld;
typedef pair<int, int> PII;
const int inf = 0x3f3f3f;
//如果能确定一只奶牛的排名,那么在他前面的奶牛和在他后面的奶牛的数量是n-1
//所以用Floyd可以得到一张连通图,遍历这个图找到符合条件的点即可
//所以floyd不仅可以用来求多源汇最短路,还可以得到一张连通图
int n, m;
int g[110][110];
void floyd(){
for(int k = 1;k <= n;++k)
for(int i = 1;i <= n;++i)
for(int j = 1;j <= n;++j)
g[i][j] = min(g[i][j], g[i][k] + g[k][j]);
}
int main()
{
ios_base::sync_with_stdio(false);
cin.tie(NULL);cout.tie(NULL);
//
cin >> n >> m;
for(int i = 1;i <= n;++i){
for(int j = 1;j <= n;++j){
if(i == j) g[i][j] = 0;
else g[i][j] = inf;
}
}
while(m--){
int a, b;cin >> a >> b;
g[a][b] = 1;
}
floyd();
int ans = 0;
int cnt = 0;
for(int i = 1;i <= n;++i){
cnt = 0;
for(int j = 1;j <= n;++j){
if((g[i][j] != inf) && (i != j)) cnt++;
}
for(int j = 1;j <= n;++j){
if((g[j][i] != inf) && (i != j)) cnt++;
}
if(cnt == n-1) ans++;
}
cout << ans << endl;
return 0;
}
后话
Floyd不仅可以用来求多源汇最短路,还可以用来检查点与点之间的连通关系。
简单介绍一下FLoyd算法:
意思是在点A与点B中插入1~k个点,看能否将原本的两点之间的距离变小。
这个用邻接矩阵存储比较方便呢,毕竟是枚举点。
板子
void floyd(){
for(int k = 1;k <= n;++k)
for(int i = 1;i <= n;++i)
for(int j = 1;j <= n;++j)
g[i][j] = min(g[i][j], g[i][k] + g[k][j]);
}
总结
图论专题真的是全新的领域啊TAT,中间还跨越了一个一周的春节假期,学习效率比较低下,但还还最后磕磕绊绊地在开下一个专题前学完了。
图论的话感觉写起来比较板子,难度不在算法本身而在建图吧。
总结一下
数据结构:并查集。
最短路算法:Floyd、Bellmen-Ford、Dijkstra、SPFA
最小生成树算法:Prim、Kruskal



