题目描述

给定不同面额的硬币 coins 和一个总金额 amount。编写一个函数来计算可以凑成总金额所需的最少的硬币个数。如果没有任何一种硬币组合能组成总金额，返回 -1。
你可以认为每种硬币的数量是无限的。
 
示例 1：
输入：coins = [1, 2, 5], amount = 11
输出：3
解释：11 = 5 + 5 + 1
 
示例 2：
输入：coins = [2], amount = 3
输出：-1
 
示例 3：
输入：coins = [1], amount = 0
输出：0
 
提示：
 1 <= coins.length <= 12
 1 <= coins[i] <= 231 - 1
 0 <= amount <= 104
思路分析
本题拟采用动态规划算法，假设F(i)是当amount = i时所需要的最少硬币数量，此时F(0)~F(i-1)均已知，由此可得动态规划方程：

 

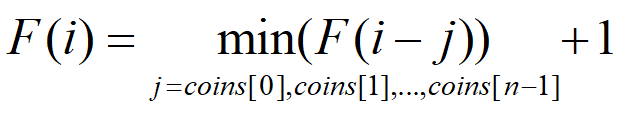
 其中j为面额硬币中的一个元素。此时动态规划算法的时间复杂度为O(Sn），S为硬币的种类。

代码实现

 1 //利用动态规划求解此题
 2 class Solution {
 3 public:   
 4     int coinChange(vector<int>& coins, int amount) {
 5         //假设需要的硬币数目比钱本身还多，说明没有合适的组成方式
 6         int MinCoins = amount + 1;
 7         vector<int> dp(amount + 1, MinCoins);
 8         dp[0] = 0;
 9         //动态规划的过程，每一个i都找到最少的硬币数量
10         for(int i = 1; i <= amount; i ++){
11             for(int j: coins){
12                 if(j <= i){
13                     dp[i] = min(dp[i], dp[i - j] + 1);
14                 }
15             }
16         }
17         //返回时判断是否有合适的组合方式
18         if(dp[amount] >= amount + 1)
19             return -1;
20         else
21             return dp[amount];
22     }
23 };