Affine 层
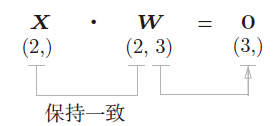
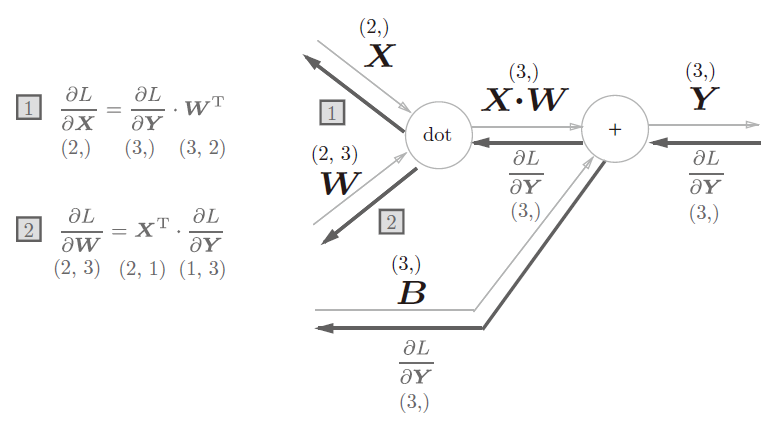
分别是形状为(2,)、(2, 3)、(3,) 的多维数组。这样一来，神经元的加权和可以用Y = np.dot(X, W) + B计算出来。
神经网络的正向传播中进行的矩阵的乘积运算在几何学领域被称为“仿射变换”。因此，这里将进行仿射变换的处理实现为“Affine层”。
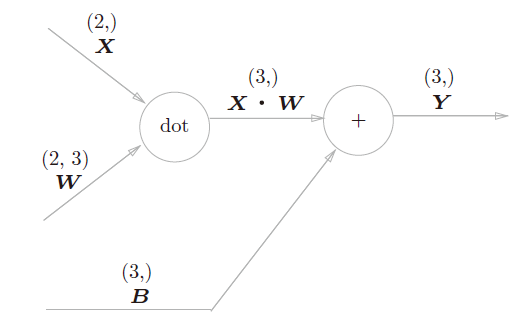
Affine层的计算图（注意变量是矩阵，各个变量的上方标记了该变量的形状）
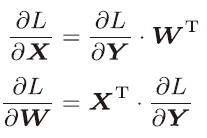
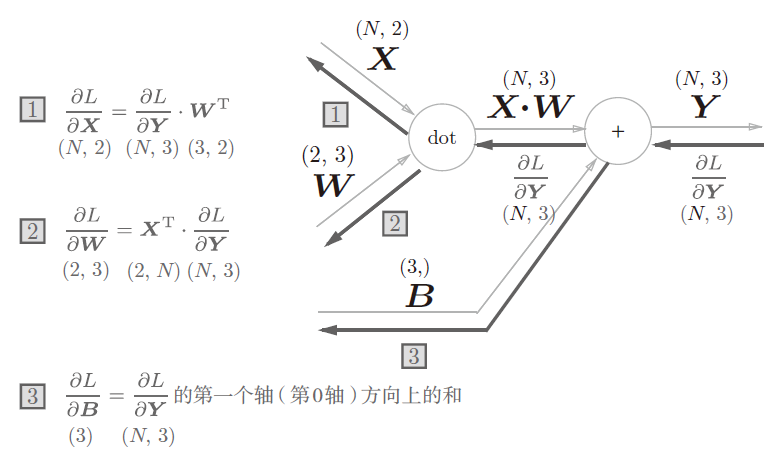
批版本的Affine 层
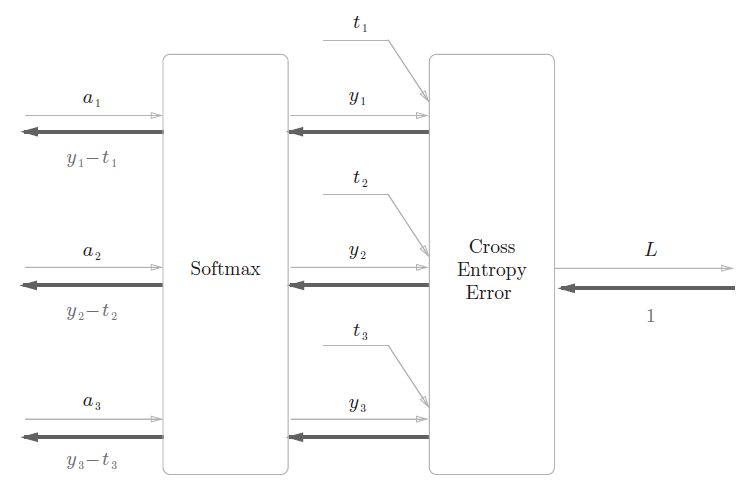
Softmax-with-Loss 层
softmax 函数会将输入值正规化之后再输出。
神经网络中进行的处理有推理（inference）和学习两个阶段。神经网络的推理通常不使用Softmax 层。神经网络中未被正规化的输出结果有时被称为“得分”。也就是说，当神经网络的推理只需要给出一个答案的情况下，因为此时只对得分最大值感兴趣，所以不需要Softmax 层。不过，神经网络的学习阶段则需要Softmax层。
使用交叉熵误差作为softmax 函数的损失函数后，反向传播得到（y1 − t1, y2 − t2, y3 − t3）这样“ 漂亮”的结果。实际上，这样“漂亮”的结果并不是偶然的，而是为了得到这样的结果，特意设计了交叉熵误差函数。回归问题中输出层使用“恒等函数”，损失函数使用“平方和误差”，也是出于同样的理由（3.5 节）。也就是说，使用“平方和误差”作为“恒等函数”的损失函数，反向传播才能得到（y1 −t1, y2 − t2, y3 − t3）这样“漂亮”的结果。
