数值微分

        像这样的由全部变量的偏导数汇总而成的向量称为梯度（gradient），梯度可以像下面这样来实现,这里使用的是用数值微分求梯度的方法。

def numerical_gradient(f, x):
    h = 1e-4 # 0.0001
    grad = np.zeros_like(x) # 生成和x形状相同的数组
    for idx in range(x.size):
        tmp_val = x[idx]

        # f(x+h)的计算
        x[idx] = tmp_val + h
        fxh1 = f(x)

        # f(x-h)的计算
        x[idx] = tmp_val - h
        fxh2 = f(x)

        grad[idx] = (fxh1 - fxh2) / (2*h)
        x[idx] = tmp_val # 还原值

    return grad                        

梯度法 

        虽然梯度的方向并不一定指向最小值，但沿着它的方向能够最大限度地减小函数的值。因此，在寻找函数的最小值（或者尽可能小的值）的位置的任务中，要以梯度的信息为线索，决定前进的方向。

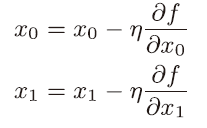
      η 表示更新量，在神经网络的学习中，称为学习率（learning rate）。学习率决定在一次学习中，应该学习多少，以及在多大程度上更新参数。

     用Python来实现梯度下降法：

def gradient_descent(f, init_x, lr=0.01, step_num=100):
    x = init_x

    for i in range(step_num):
        grad = numerical_gradient(f, x)
        x -= lr * grad

    return x    

      f 是要进行最优化的函数，init_x 是初始值，lr 是学习率learningrate，step_num 是梯度法的重复次数。numerical_gradient(f,x) 会求函数的梯度，用该梯度乘以学习率得到的值进行更新操作，由step_num 指定重复的次数。

    像学习率这样的参数称为超参数。

神经网络的梯度

   神经网络的学习也要求梯度。这里所说的梯度是指损失函数关于权重参数的梯度

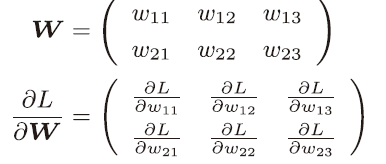
     的元素由各个元素关于W的偏导数构.