树状数组理解
前言
树状数组,顾名思义,一个“树状”的数组,如下图
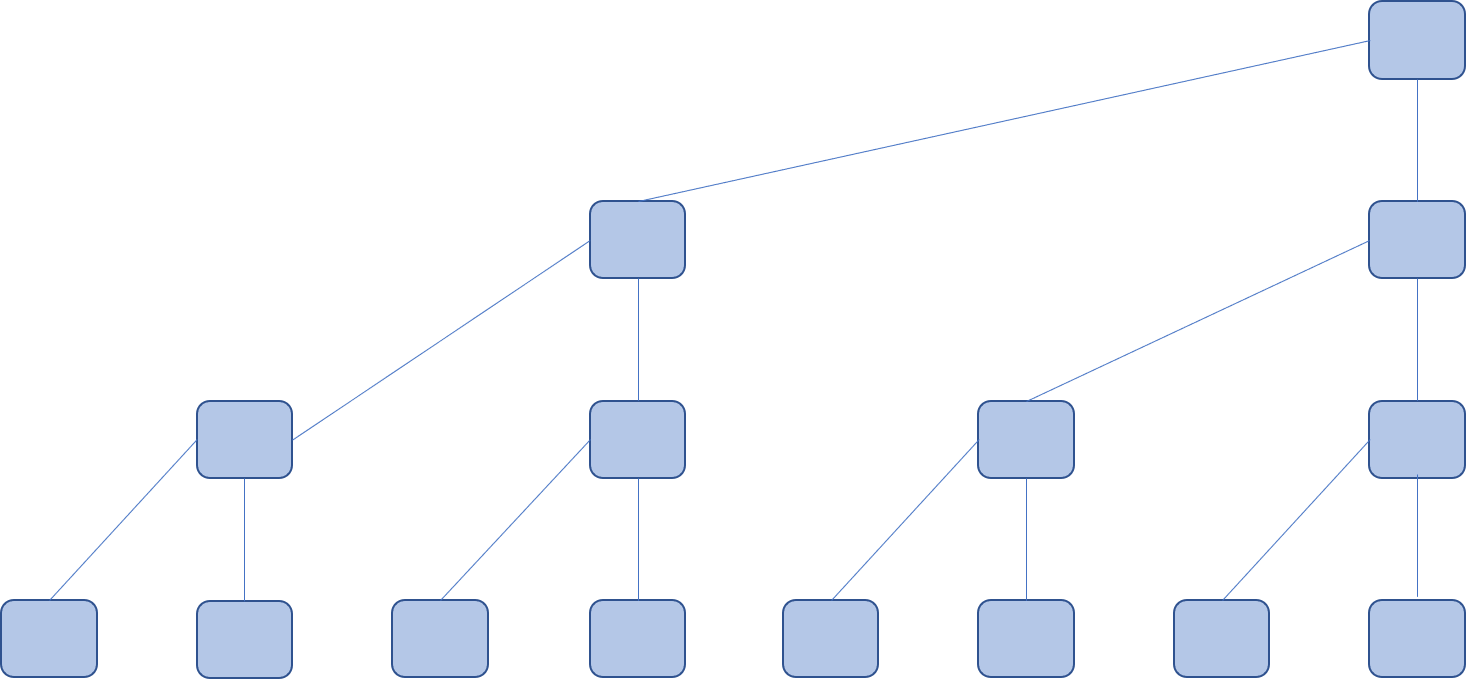
它就是一个"靠右"的二叉树,树状数组是一个查询和修改复杂度都为log(n)的数据结构。
主要用于数组的修改and求和。
树状数组与线段树
树状数组能完成的线段树都能完成,线段树能完成的树状数组不一定能完成,但是树状数效率更高。
二者复杂度同级,但是树状数组编程效率更高,利用lowbit技术,使得树状数组能很好实现。
注意:本文章下标都从1开始
一维树状数组
实现
规律
对于一个数组A,将它看成一个初始的序列,通过它来实现树状数组C,如下图
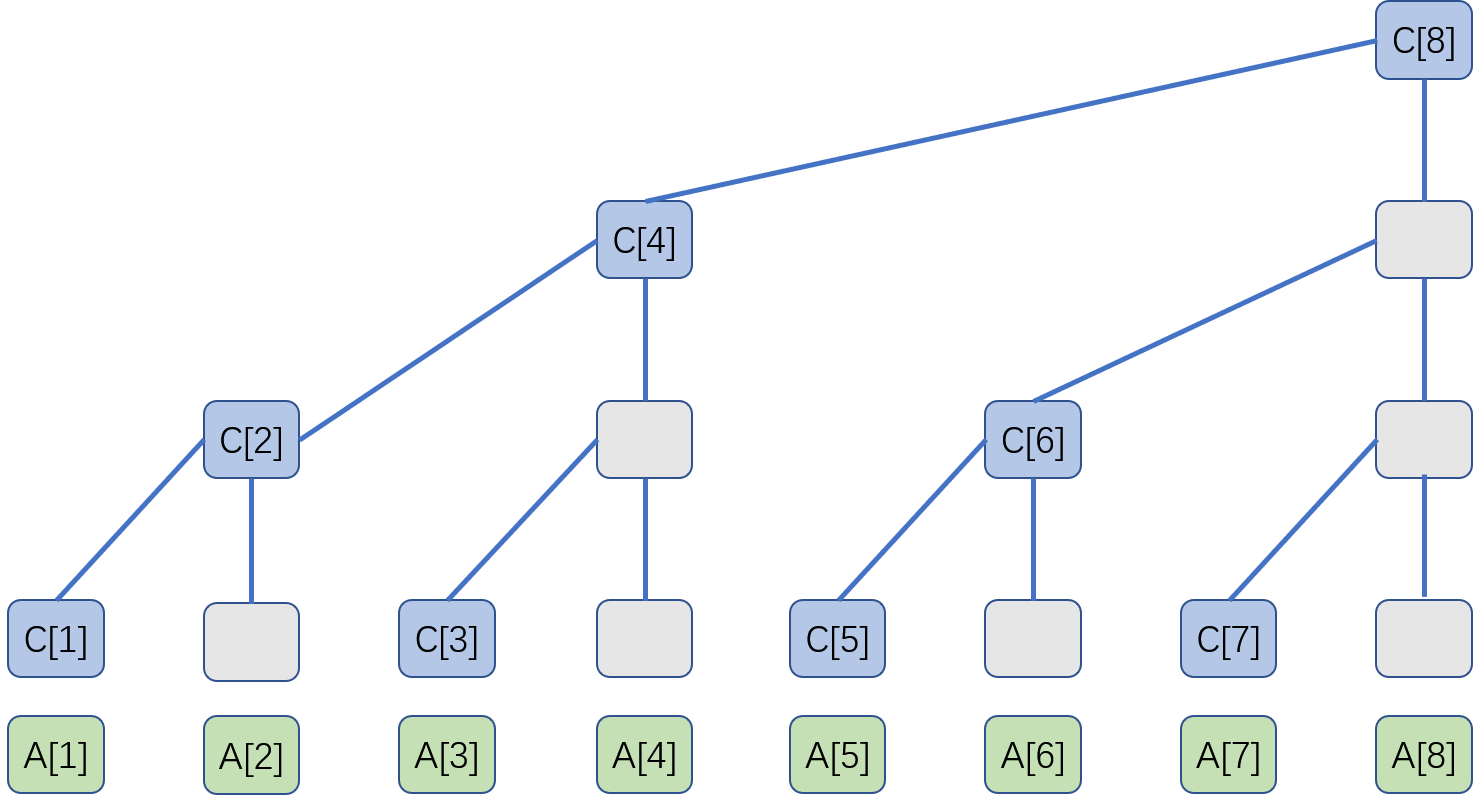
省去二叉树的一些节点,以达到用数组建树。
通过上图可得:
- C[1] = A[1];
- C[2] = A[1] + A[2]
- C[3] = A[3];
- C[4] = A[1] + A[2] + A[3] + A[4]
- C[5] = A[5];
- C[6] = A[5] + A[6]
- C[7] = A[7];
- C[8] = A[1] + A[2] + A[3] + A[4] + A[5] + A[6] + A[7] + A[8]
找规律:下标i
- 为奇数时,C[ i ]=A[ i ]
- 为2的倍数但不为4的倍数时,C[ i ]=A[i-1]+A[i]
- 为4的倍数时,C[ i ]=A[1]+A[2]+...+A[ i ]
将C数组的下标转化为二进制
-
1=(001) C[1]=A[1];
-
2=(010) C[2]=A[1]+A[2];
-
3=(011) C[3]=A[3];
-
4=(100) C[4]=A[1]+A[2]+A[3]+A[4];
-
5=(101) C[5]=A[5];
-
6=(110) C[6]=A[5]+A[6];
-
7=(111) C[7]=A[7];
-
8=(1000) C[8]=A[1]+A[2]+A[3]+A[4]+A[5]+A[6]+A[7]+A[8];
可以发现
C[ i ] = A[i - 2k+1] + A[i - 2k+2] + ... + A[i]
k为i的二进制中从最低位到高位连续零的长度
比如i=8,k=3,C[ 8 ]=A[1]+A[2]+...+A[8]
联系上面规律和二进制,可得
C数组下标i的二进制截取从最右端一位到从右往左第一个1的这一段表示的十进制数就是C[ i ]所存的A数组中元素的个数的和。
也就是C[ i ]存A数组中2k个元素的和,截取的一段=2k
比如:
- C[2],二进制为10,截取的就是10,k=1,换成10进制就是2,表示存两个数的和,也就是A[1]+A[2]
- C[4],二进制为100,截取的就是100,k=2,换成10进制就是4,表示存四个数的和,也就是A[1]+A[2]
- C[5],二进制为101,截取的就是1,k=0,换成10进制就是1,表示存一个数的和,也就是A[5]
现在C的建造式已经得到,剩下就考虑如何得到k
lowbit函数
既然k为i的二进制中从最低位到高位连续零的长度,那么可以想到用计算机补码的思想
负数的二进制等于对应的正数的二进制按位取反后加一,
比如:
t=5(101)
-t=-5(010+1)=011
然后再利用按位与得出k
101
011
按位与得出001,即k=0
x&(-x),即k,当x为0时结果为0;x为奇数时,结果为1;x为偶数时,结果为x中2的最大次方的因子。
int lowbit(int x){
return x&(-x);
}
上面函数的返回值就是2k。
设x=lowbit( i )
C[ i ]=A[ i ]+A[i-1]+...+A[i-x+1](共x个数)
先初始化C数组为零,然后开始接下来的操作。
操作一:单改区查
理解了上面的讲解,下面的操作就好办了
单点更新
当更新A数组的一个元素时,要考虑C数组中所有与A中更新元素有关系的元素。
如图:
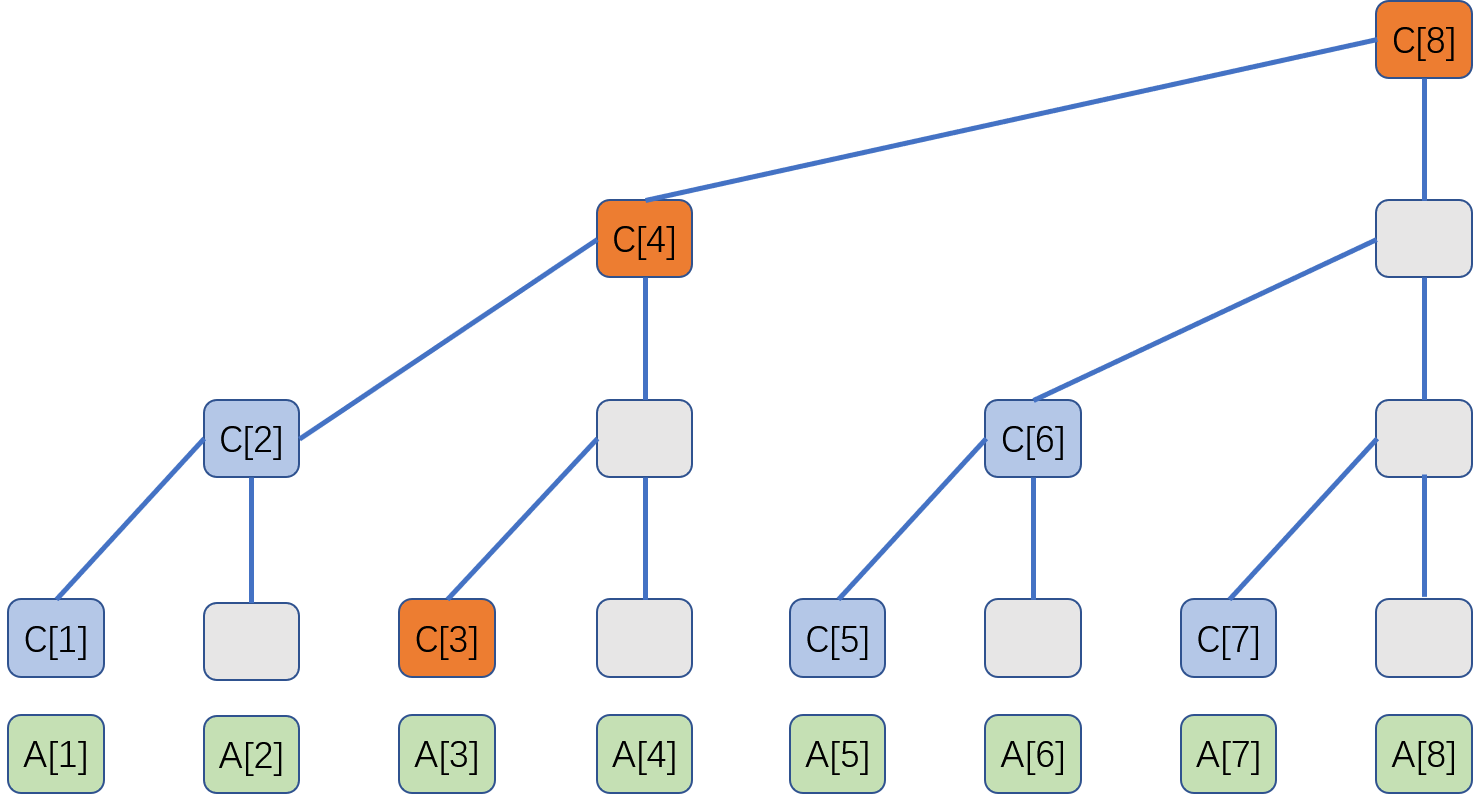
更新A[3]时,C[3]、C[4]、C[8]也需要更新
也就是,假设A[3]改变了k
- C[3]+=k C[011]+=k
- lowbit(3)=1=001 C[4]+=k C[011+001]+=k
- lowbit(4)=4=100 C[8]+=k C[100+100]+=k
void updata(int n,int x){//n为修改的位置,x为修改的值 for(int i=n;i<=max_n;i+=lowbit(i)){ C[i]+=x; } }
总的来说如果我们更新某个A[i]的值,则会影响到所有包含有A[i]位置。有A[i] 包含于 C[i + 2k]、C[(i + 2k) + 2k] ...
- 不妨来看看lowbit(0)=0,如果下标从零开始,那么更新C[0]的时候,0+lowbit(0)=0,下标始终为零,更新不到数组的更高层,而且程序也会陷入死循环,所以下标从1开始
区间查询
假设:如果要查询A[1]到A[5]的和
就有:
C[4]=A[1]+A[2]+A[3]+A[4]
C[5]=A[5]
sum(5)=C[5]+C[4]
也就是
x=lowbit(5)=1
101-x=100
sum(5)=C[101]+C[100]
所以联系上面,区间查询就可以看成区间更新的逆操作
如果查询点为n,则需要查询的就是C[n]+C[n-lowbit(n)]+...直到下标等于0
int getsum(int n){//n为查询点
int sum=0;
for(int i=n;i>0;i-=lowbit(i)){
sum+=C[i];
}
return sum;
}
最终程序
一个算法最重要的是什么,当然是板子(滑稽.jpg)
1 #include<iostream>
2 using namespace std;
3 const int max_n=1<<16;
4 int C[max_n]={0};
5 //查询
6 int getsum(int n){
7 int sum=0;
8 for(int i=n;i>0;i-=lowbit(i)){
9 sum+=C[i];
10 }
11 return sum;
12 }
13 //更新
14 void updata(int n,int x){
15 for(int i=n;i<=max_n;i+=lowbit(i)){
16 C[i]+=x;
17 }
18 }
19 //适合单点更新和区间查询
上面代码只适合单点更新和区间查询,如何想要更多操作,则需要更高级的思考了
操作二:区改单查
接下来的操作可能会和上面的操作差不多,但是更难想到,对于我,只能说前人的智慧太精深了(赞叹!),至于为什么,看接下来的内容
前言
学习了上面的单点更新,可能就会和我一样,觉得区间更新就是把一个区间的点一个一个的更新,想法不算错,但是却没有考虑到树状数组的初心和充分利用。
一个一个点的更新,那么复杂会很高。
利用树状数组的特性,我们可以有更好的方法来实现——建立差分数组
设中间差分数组D,D[ i ]=A[ i ]-A[i-1](1<=i<=n)
那么就用D数组来建立C这个树状数组
区间查询
演算
假设
A[8]={1,3,4,5,6,8,8,9}
那么
D[8]={1,2,1,1,1,2,0,1}
C[8]={1,3,1,5,1,3,0,15}
需要更新的区间为[2,5],更新的值为k=2
则
D数组改变为
1 4 1 1 1 0 0 1
C数组改变为
1 5 1 7 1 1 0 17
可以看出,修改A的区间时,对D来说只是改变了2和6的值
- 也就是说修改区间[ l, r],则D[ l ]+2,D[r+1]-2,对于一个很大的区间,却只需要更新两个点 !!!
- 对于区间[ l, r]和k,updata(l,k) 和 updata(r+1,-k)
这就体现了前人的智慧,极大的降低复杂度。
实现
前人种树,后人乘凉。
有了差分数组,就好办事了。
区间更新就是更新差分数组的两个点,接下来就是用操作一来实现了
void updata(int n,int k){
for(int i=n;i<max_n;i+=lowbit(i)){
C[i]+=k;
}
}
int main(){
int n,l,r,k,a,t;
cin >> n;
cin >> a;
for(int i=1;i<=n;i++){
if(i==1){
updata(1,a);
continue;
}
cin >> t;
updata(i,t-a);//构造虚拟D[]数组差分来创建C[]数组
a=t;
}
cin >> l >> r >> k;
//l---r区间更新 k
updata(x,k);//D[l]+k;
updata(y+1,-k);//D[r+1]-k;
return 0;
}
单点查询
有人会说,直接用原数组不就行了吗。。。
说的没错。我最初也很疑问
但是没必要,因为更新树状数组的时候,完全可以省去原数组的空间,达到时间、空间优化。
假设现在要查询x点
- 因为D[ i ]=A[ i ] - A[i-1]
- 所以A[x]=D[1]+D[2]+ ... +D[ x ]
- 又因为上面讲过C[ i ] = D[i - 2k+1] + D[i - 2k+2] + ... + D[ i ]
- 所以A[x]=C[x]+C[x-lowbit(x)]+ ... ,而这不就是getsum函数吗。。。
所以最后发现查询一个点就是函数getsum(x)
int getsum(int i){
int ans=0;
while(i>0){
ans+=C[i];
i-=lowbit(i);
}
return ans;
}
还有一件事:如果使用树状数组的话,还有原数组保留的话,区间修改只能修改到树状数组,而不会修改原数组,所以不能直接查询原数组。
所以,还是getsum吧。。。
总结
用差分形式,需要在数据输入的时候就对树状数组进行更新。
对于区间修改,则需要在区间原有数据的情况下,每一个元素都要修改相同的值,
而如果要给区间重新赋值,那就最好不要用树状数组了。
操作三:区改区查
显然,这个操作也需要创造差分数组
前言
区改区查有和区改单查一样的区间修改,但是却多了区间查询。
学习了上面的操作,看到区间查询,我想第一反应是有更好的方法来实现,而不是一个一个的进行单点查询
既然有相同的区间修改的特性,索性就直接从区间查询开始吧,建议开始下面的学习时,先把上面的操作二弄懂
区间查询
依然是A原数组,D差分数组,C树状数组,有
A[1]+A[2]+A[3]+...+A[n] = D[1]+ (D[1]+D[2]) + (D[1]+D[2]+D[3]) + ... +(D[1]+D[2]+D[3]+...+D[n])
变换一下
$\sum_{i=1}^{n} A[i]$ = n*D[1] + (n-1)*D[2] + (n-2)*D[3]+...+D[n]
=n*( D[1]+D[2]+D[3]+...+D[n] ) - ( 0*D[1] + 1*D[2] + ... + (n-1)*D[ n ] )
最后
$\sum_{i=1}^{n}A[i]=n*\sum_{i=1}^{n}D[i]-\sum_{i=1}^{n}(D[i]*(i-1))$
所以我们除了用D数组来创造C数组以外,还需要用D[ i ]*( i-1)来创造一个CX数组
也就是维护两个树状数组,只C是用差分来创建数组,而CX朴素的树状数组,这需要分清楚。
- 在更新C数组的同时,更新CX数组
- 查询[ l,r ]时,只需getsum(y)-getsum(x-1)
注意:
此时因为有了CX数组,所以getsum函数和updata函数要考虑到CX的更新和求和
具体看代码吧:
#include<iostream>
using namespace std;
const int max_n=1<<16;
int A[max_n]={0};
int C[max_n]={0};
int CX[max_n]={0};
int lowbit(int i){
return i&(-i);
}
void updata(int i,int k){
int x=i;//因为 CX[]是树状数组,所以要保存初始 i
// 更新一个值,其他的bitelse也要更新相同的值
while(i<max_n){
C[i]+=k;
CX[i]+=k*(x-1);
i+=lowbit(i);
}
}
int getsum(int i){
int ans=0,x=i;
while(i>0){
ans+=x*C[i]-CX[i];
i-=lowbit(i);
}
return ans;
}
int main(){
int n,x,y,k,z;
cin >> n;
for(int i=1;i<=n;i++){
cin >> A[i];
updata(i,A[i]-A[i-1]);
}
cin >> x >> y >> k;
updata(x,k);//更新D[x];
updata(y+1,-k);//更新D[y+1]
int sum=getsum(y)-getsum(x-1);
cout << sum;//求x---y区间的和
return 0;
}
二维树状数组
实现
二维树状数组只是将一维拓展成二维,只需要将原来的一维循环化成二维而已。
单改区查
C这个树状数组中的某个元素C[x]记录的是右端点为x,长度为lowbit(x)的区间和。
那么二维树状数组C[x][y]记录的是右下端点为[x,y],高为lowbit(x),宽为lowbit(y)的矩形范围的区间和。
代码如下
int lowbit(int x){
return x&(-x);
}
void updata(int x, int y, int z){ //将点(x, y)加上z
int now_y = y;
while(x <= n){
y = now_y;
while(y <= n) C[x][y] += z, y += lowbit(y);
x += lowbit(x);
}
}
int query(int x, int y){//求左上角为(1,1)右下角为(x,y) 的矩阵和
int res = 0, now_y= y;
while(x){
y = now_y;
while(y) res += C[x][y], y -= lowbit(y);
x -= lowbit(x);
}
return res;
}
文章总结
博主就只会这些了。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号