[数据结构-树状数组小结]

树状数组又叫二叉索引树

参考《训练指南》P194

动态求连续区间和，可以动态更新数据，支持以下两种操作：

1、 对某一元素进行更新操作。

2、 查询某一连续区间的元素和。

对于正整数x，我们定义lowbit(x)为“x的二进制表示中最右边的1所表示的值”，例如lowbit(11001100) =100 （这里的11001100、100都是二进制表示），在程序实现中lowbit(x) = x&-x ，原因如下。

x  0000 0000 1100 1100

-x 1111 1111 0011 0100 ---反码加1，称为补码

lowbit(16) = 16

lowbit(8) = 8

lowbit(4) = 4

lowbit(2) = 2

lowbit(1) = 1

A数组下标从1开始。

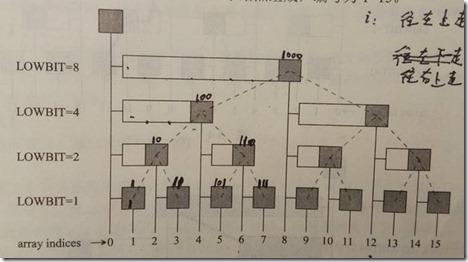
每一层lowbit值相同，下面构造辅助数组C，C[i] = A[i-lowbit(i)+1] + A[i-lowbit(i)+2] +…..+ A[i]。

C[1]=A[1]

C[2]=A[1]+A[2]

C[3]=A[3]

C[12]=A[9]+A[10]+A[11]+A[12]

C[i]就是以i结尾的白条（看上图）

两个操作的代码如下：

int sum(int x)   //求前缀和，x向左上爬
{
    int ret=0;
    while(x>0)
    {
        ret+=C[x];
        x-=lowbit(x);
    }
    return ret;
}

 

void add(int x,int d)  {  //A[x]加上d，x向右上爬
    while(x<=n) {
        c[x]+=d;
        x+=lowbit(x);
    }
}

 

不难证明，两个操作都是log(n)，而预处理操作相当于执行了n次add操作，所以总复杂度是nlog(n)。

完结。