【注意力机制】Attention Augmented Convolutional Networks

注意力机制之Attention Augmented Convolutional Networks

原始链接：https://www.yuque.com/lart/papers/aaconv

image.png

核心内容

We propose to augment convolutional operators with this self-attention mechanism by concatenating convolutional feature maps with a set of feature maps produced via self-attention.

主要工作

首先了解卷积操作本身两点特性:

尽管这些属性被证明了是设计在图像上操作的模型时至关重要的归纳偏置(inductive biase). 但是卷积的局部性质(the local nature of the convolutional kernel)阻碍了其捕获全局的上下文信息(global context), 而这些信息对于图像识别是很必要的. 这是卷积的重要的弱点. (convolution operator is limited by its locality and lack of understandingof global contexts)

而在捕获长距离交互关系(long range interaction)上, 最近的Self-attention表现的很不错(has emerged as a recent advance). 自注意力背后的关键思想是生成从隐藏单元计算的值的加权平均值. 不同于卷积操作或者池化操作, 这些权重是动态的根据输入特征, 通过隐藏单元之间的相似性函数产生的(produced dynamically via a similarity function between hidden units). 因此输入信号之间的交互依赖于信号本身, 而不是像在卷积中, 被预先由他们的相对位置而决定.

所以本文尝试将自注意力计算应用到卷积操作中, 来实现长距离交互. 在判别性视觉任务(discriminative visual tasks)中, 考虑使用自注意力替换普通的卷积. 引入a novel two-dimensional relative self-attention mechanism, 其在注入(being infused with)相对位置信息的同时可以保持translation equivariance, 使其非常适合图像.

在取代卷积作为独立计算单元方面被证明是有竞争力的. 但是需要注意的是, 在控制实验中发现, 将自注意力和卷积组合起来的情况可以获得最好的结果. 因此并没有完全抛弃卷积, 而是提出使用self-attention mechanism来增强卷积(augment convolutions), 即将强调局部性的卷积特征图和基于self-attention产生的能够建模更长距离依赖(capable of modeling longer range dependencies)的特征图拼接来获得最终结果.

在多个实验中, 注意力增强卷积都实现了一致的提升, 另外对于完全的自注意模型(不用卷积那部分), 这可以看作是注意力增强模型的一种特殊情况, 在ImageNet上仅比它们的完全卷积结构略差, 这表明自注意机制是一种用于图像分类的强大独立的计算原语(a powerful standalone computational primitive).

关于primitive这个概念, 找到了一段解释: 大意是指整个系统中最基本的概念.
https://stackoverflow.com/a/8022435
For me, it means something that cannot be decomposed (people use also the atomic word sometimes in that sense, but atomic is often also used for explanation on concurrency or parallelism with a different meaning).​
For instance, on Unix (or Linux) the system calls, as seen by the application are primitive or atomic, they either happen or not (sometimes, they got interrupted and give an EINTR or ERESTART error).
And inside an interpreter, or even in the formal specification, of a language, the primitive are those operations which you cannot define, and which the interpreter deals with specially. Very often, cons is a primitive operation for Lisp dialects.

这里提到了其他的一些visual tasks中的注意力的工作:

相对于现有的方法, 这里要提出的结构不依赖于对应的(counterparts)完全卷积模型的预训练, 而是整个网络都使用了self-attention mechanism. 另外multi-head attention的使用使得模型同时关注空间子空间和特征子空间. (多头注意力就是将特征划沿着通道划分为不同的组, 不同组内进行单独的变换, 可以获得更加多样化的特征表达)

另外, 为了增强图像上的自注意力的表达能力, 这里扩展[Selfattention with relative position representations,  Music transformer]中的相对自注意力到二维形式, 这使得可以以有原则(in a principled way)地模拟平移等变性(translation equivariance).

这样的结构可以直接产生额外的特征图, 而不是通过加法(可能是乘法)[Non-local neural networks,  Self-attention generative adversarial networks]或门控[Squeeze-and-excitation networks, Gather-excite: Exploiting feature context in convolutional neural networks, Bam: bottleneck attention module, Cbam: Convolutional block attention module]重新校准卷积特征. 这一特性允许灵活地调整注意力通道的比例, 考虑从完全卷积到完全注意模型的一系列架构(a spectrum of architectures, ranging from fully convolutional to fully attentional models).

主要结构

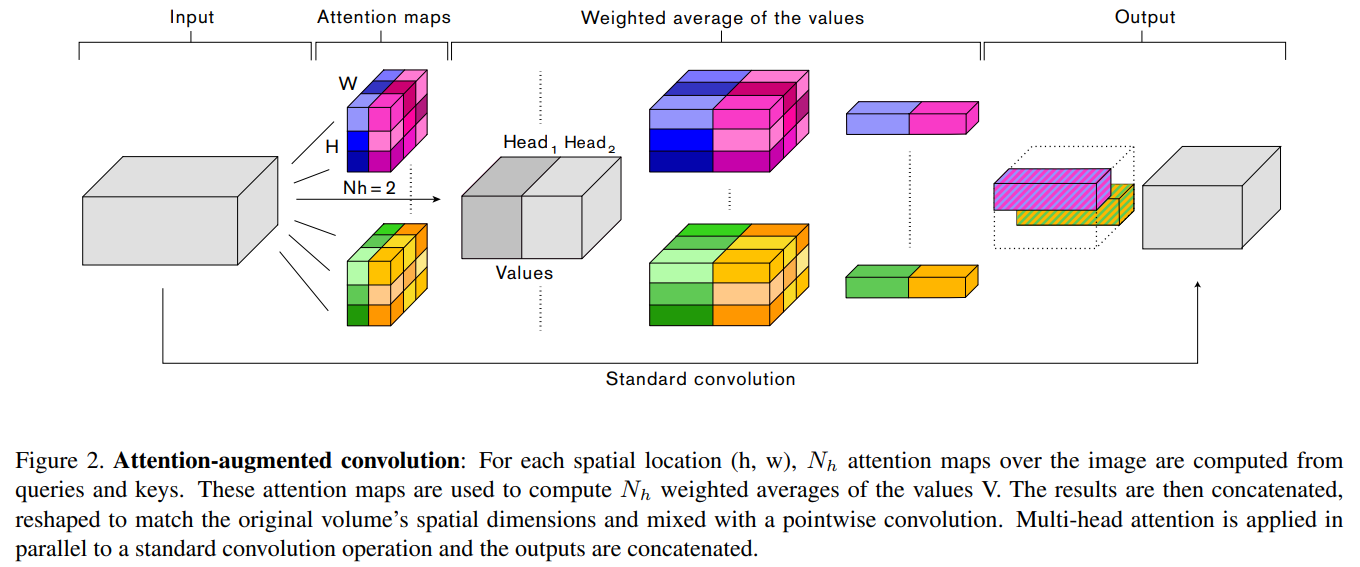
image.png

  • H, W, Fin: 输入特征图的height, weight, 通道数
  • Nh, dv, dk:heads的数量, values的深度(也就是特征图通道数), queries和keys的深度(这几个参数都是MHA, multi-head attention的一些参数), 这里有要求, dv和dk必须可以被Nh整除, 这里使用dhv和dhk来作为每个head中值的深度和查询/键的深度

图像数据多头注意力的计算

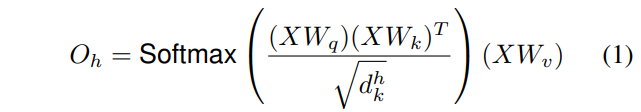
image.png

单头的计算形式

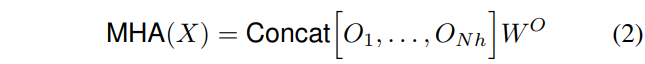
image.png

多头是由单头拼接而成

  1. in_tensor\((H,W,F_{in})\) =(flatten)=> X\((HW,F_{in})\)(We omit the batch dimension for simplicity.)
  2. 按照transformer结构结算多头注意力
    1. 对于head h对应的自注意力结果为式子1所示, 这里的\(W_q\)/\(W_k\)/\(W_v\)分别形状为\((F_{in}, d^h_q)/(F_{in}, d^h_k)/(F_{in}, d^h_v)\), 分别用于映射输入X到查询\(Q=XW_q\) 、键\(K=XW_k\) 和值\(V=XW_v\) , 分别的形状为\((HW, d^h_q)/(HW, d^h_k)/(HW, d^h_v)\)​
    2. 所有head的输出拼接到一起, 然后按照式子2进行处理, 这里的\(W^O \in \mathbb{R}^{d_v \times d_v}\)(可以知道, 这里的\(N_h\)个\(O\)的拼接, 实际上深度为\(d_v\), 也就是\(d_v=N_h \times d^h_v\)), 这里MHA计算后会调整形状为\((H, W, d_v)\)来匹配原始的空间维度
    3. multi-head attention
      1. 计算复杂度：\(O((HW)^2d_k)\)(这里只需要考虑大头\((XW_q)(XW_k)^T\)的计算)
      2. 空间复杂度：\(O((HW)^2N_h)\)(这里包含了Nh个头的结果)

二维位置嵌入Two-dimensional Positional Embeddings

这里的"二维"实际上是相对于原始针对语言的一维信息的结构而言, 这里输入的是二维图像数据.

由于没有显式的位置信息的利用, 所以自注意力满足交换律:\(MHA(\pi(X))=\pi(MHA(X))\), 这里的\(\pi\)表示对于像素位置的任意置换. 这反映出来self-attention具有 permutation equivariant. 这样的性质使得对于模拟高度结构化的数据(例如图像)而言, 不是很有效.

多个使用显式的空间信息来增强激活图的位置编码已经被提出来处理相关的问题:

  1. Image Transformer extends the sinusoidal waves first introduced in the original Transformer to 2 dimensional inputs.
  2. CoordConv concatenates positional channels to an activation map.

在文章的实验中发现, 在图像分类和目标检测上, 这些编码方法并不好用, 作者们将其归因于虽然这些策略可以打破置换等变性, 但是却不能保证图像任务需要的平移等变性(permutation equivariant(置换等变性), translation equivariance(平移等变性)). 为此, 这里扩展了现有的相对位置编码[Self attention with relative position representations]到二维上, 并且基于Music Transformer提出一个内存有效的实现.

相对位置嵌入Relative positional embeddings

Introduced in [Self attention with relative position representations] for the purpose of language modeling, relative self-attention augments self-attention with relative position encodings and enables translation equivariance while preventing permutation equivariance.

这里通过独立添加相对的宽和相对的高的信息, 来实现二维相对自注意力.
对于像素\(i=(i_x, i_y)\)关于像素\(j=(j_x, j_y)\)的attention logit计算方式如下(The attention logit for how much pixel i attends to pixel j is computed as):

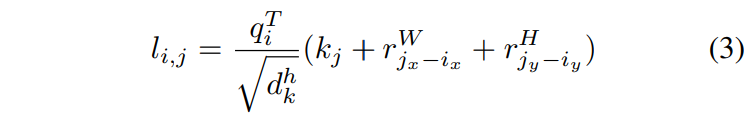
image.png

  • \(q_i\)表示 位置为\(i\) 的query vector, 也就是Q中的一个长为\(d^h_k\)的矢量元素.
  • \(k_j\)表示 位置为\(j\) 的key vector, 也就是K中的一个长为\(d^h_k\)的矢量元素.
  • \(r^W_{j_x-i_x}\)和\(r^H_{j_y-i_y}\)表示对于相对宽度\(j_x-i_x\)和相对高度\(j_y-i_y\)学习到的嵌入表示, 各自均为dhk长度的矢量.
  • \(r\)对应的相对位置参数矩阵\(r^W\)和\(r^H\)分别是\((2W-1, d^h_k)\)和\((2H-1, d^h_k)\)大小的.

单个头h的输出变成了:

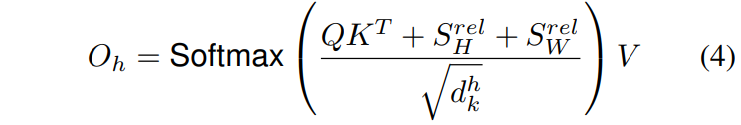
image.png

这里的两个\(S\)都是\(HW \times HW\)的矩阵, 表示沿着宽高维度的相对位置logits

  • image.png
  • image.png

因为考虑相对宽高信息, 所以满足\(S^{rel}_W[i, j]=S^{rel}_W[i, j+W]\),\(S^{rel}_H[i, j]=S^{rel}_H[i, j+H]\). 这样就不需要为所有的(i, j)对计算logits了, 这里可以按照这样来理解(这是我自己的理解): 对于二维矩阵, 按照沿着行为W方向(横向), 也即是x方向, 沿着列为H方向(纵向)即y向, 对于任意一点\(j\)和固定的点\(i\):

  • SW中有\((j_x-i_x)\%W=[(j+nW)_x-i_x]\%W\), 即按照行主序向后移动个位置, 仍位于同一列;
  • SH中有\((j_y-i_y)\%H=[(j+nH)_y-i_x]\%H\), 即按照列主序向后移动\(nH\)个位置, 依然在同一行.

这里的相对注意力的形式实际上不同于原始参考论文Self attention with relative position representations中具有内存占用为\(O((HW)^2d^h_k)\)(相对嵌入\(r_{ij} \in \mathbb{R}^{HW \times HW \times d^h_k}\))的设计, 而是基于MUSIC TRANSFORMER中提出的memory efficient relative masked attention algorithm的一种2D扩展, 扩展为了unmasked relative self-attention over 2 dimensional inputs上, 从而存储消耗变成了\(O(HWd^h_k)\)(相对位置嵌入\(r_{ij}\)被拆分成两个部分, 即\(r^H \in \mathbb{R}^{(2H-1) \times d^h_k}, r^W \in \mathbb{R}^{(2W-1 )\times d^h_k}\), 并且跨头不跨层的形式进行共享). 对于每层, 实际上只需要添加额外的\((2(H + W) − 2)d^h_k\)个参数来建模沿着高和宽的相对距离即可.

Attention Augmented Convolution

文章提出的使用注意力增强的卷积主要的优势:

  1. use an attention mechanism that can attend jointly to spatial and feature subspaces (each head corresponding to a feature subspace)
  2. introduce additional feature maps rather than refining them

AAConv的主要过程:

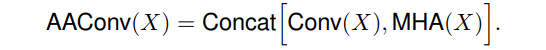
image.png

Similarly to the convolution, the proposed attention augmented convolution

  1. is equivariant to translation
  2. can readily operate on inputs of different spatial dimensions

接下来对标一般的卷积\((F_{out}, F_{in}, k, k)\)分析了AAConv的参数量:

  • 设置\(v=\frac{d_v}{F_{out}}\)作为MHA部分的总输出通道数与总的AAConv输出通道数的比值;
  • 设置\(\kappa = \frac{d_k}{F_{out}}\)作为MHA中Key的深度与总的AAConv输出通道数的比值.
  • 使用\(1 \times 1\)卷积来线性变换得到Q\K\V, 所以有参数量\((d_v+d_k+d_q)F_{in} = (2d_k+d_v)F_{in}=(v+2\kappa)F_{out}F_{in}\)
  • 使用一个额外的\(1\times1\)卷积用于混合多个头的贡献(mix the contribution of different heads), 这部分参数量为\(d_vd_v=(vF_{out})^2\);
  • 除了注意力部分, 还有一部分标准卷积, 即前面式子中的Conv, 其参数量为:\(k^2(F_{out} - d_v)F_{in} = k^2(1 - v)F_{out}F_{in}\);
  • 所以, 忽略了相对位置嵌入和卷积偏置之后, 整体的结构的参数量约为:\(F_{in}F_{out}(2\kappa+v+v^2\frac{F_{out}}{F_{in}}+k^2-k^2v)=F_{in}F_{out}(2\kappa+v(1-k^2)+k^2+v^2\frac{F_{out}}{F_{in}})\)
  • 整体相对于卷积的参数的变化量为\(\Delta_{params}\sim F_{in}F_{out}(2\kappa+v(1-k^2)+v^2\frac{F_{out}}{F_{in}})\), 所以替换3x3卷积时, 会轻微减少参数量, 而替换1x1卷积时, 则会带来轻微的增加.

Attention Augmented Convolutional Architectures

  • 所有实验中, AAConv后都会跟着BN来放缩卷积层和注意力层特征图的共享.
  • 每个残差块使用一次AAConv.
  • 由于QK的结果具有较大的内存占用, 所以是按照从深到浅的顺序使用, 直到达到内存上限.
  • To reduce the memory footprint of augmented networks, we typically resort to a smaller batch size and sometimes additionally downsample the inputs to self-attention in the layers with the largest spatial dimensions where it is applied(这里指的应该是在注意力计算前后分别下采样和上采样). Downsampling is performed by applying 3x3 average pooling with stride 2 while the following upsampling (requiredfor the concatenation) is obtained via bilinear interpolation.

实验结果

位置编码

image.png

image.png

  • the position-unaware version of self-attention (referred to as None),
  • a two-dimensional implementation of the sinusoidal positional waves (referred to as 2d Sine) as used in [32],
  • CoordConv [29] for which we concatenate (x, y, r) coordinate channels to the inputs of the attention function,
  • our proposed two-dimensional relative position encodings (referred to as Relative).

未来的探索

  • Several open questions from this work remain. In future work, we will focus on the fully attentional regime and explore how different attention mechanisms trade off computational efficiency versus representational power. For instance, identifying a local attention mechanism may result in an efficient and scalable computational mechanism that could prevent the need for downsampling with average pooling [Stand-aloneself-attention in vision models].
  • Additionally, it is plausible that architectural design choices that are well suited when exclusively relying on convolutions are suboptimal when using self-attention mechanisms. As such, it would be interesting to see if using Attention Augmentation as a primitive in automated architecture search procedures proves useful to find even better models than those previously found in image classification [55], object detection [12], image segmentation [6] and other domains [5, 1, 35, 8].
  • Finally, one can ask to which degree fully attentional models can replace convolutional networks for visual tasks.

代码示例

参照作者论文中的tensorflow实现, 我使用pytorch改了下.

import torch
from einops import rearrange
from torch import nn

def rel_to_abs(x):
    """
    Converts tensor from relative to aboslute indexing.
    Details can be found at: https://www.yuque.com/lart/ugkv9f/oazsec

    :param x: B Nh L 2L-1
    :return: B Nh L L
    """
    B, Nh, L, _ = x.shape

    # Pad to shift from relative to absolute indexing.
    col_pad = torch.zeros(B, Nh, L, 1)
    x = torch.cat([x, col_pad], dim=3)

    flat_x = x.reshape(B, Nh, L * 2 * L)

    flat_pad = torch.zeros(B, Nh, L - 1)
    flat_x = torch.cat([flat_x, flat_pad], dim=2)

    # Reshape and slice out the padded elements.
    final_x = flat_x.reshape(B, Nh, L + 1, 2 * L - 1)
    final_x = final_x[:, :, :L, L - 1:]
    return final_x

def relative_logits_1d(x, rel_k):
    """
    Compute relative logits along one dimenion.

    :param x: B Nh Hd L
    :param rel_k: 2L-1 Hd
    """
    rel_logits = torch.einsum("bndl, rd -> bnlr", x, rel_k)
    rel_logits = rel_to_abs(rel_logits)  # B Nh L 2L-1 -> B Nh L L
    return rel_logits

class RelativePosEmbedding(nn.Module):
    """
    Compute relative_logits.

    For ease, we 1) transpose height and width, 2) repeat the above steps and 3) transpose to eventually
    put the logits in their right positions.
    """

    def __init__(self, h, w, dim):
        super(RelativePosEmbedding, self).__init__()
        self.h = h
        self.w = w
        self.rel_emb_w = torch.randn(2 * w - 1, dim)
        nn.init.normal_(self.rel_emb_w, dim ** -0.5)
        self.rel_emb_h = torch.randn(2 * h - 1, dim)
        nn.init.normal_(self.rel_emb_h, dim ** -0.5)

    def forward(self, x):
        """
        :param x: B Nh Hd HW
        :return: B Nh HW HW
        """
        Nh = x.shape[1]
        # Relative logits in width dimension first.
        rel_logits_w = relative_logits_1d(
            rearrange(x, "b nh hd (h w) -> b (nh h) hd w", h=self.h, w=self.w), self.rel_emb_w
        )
        rel_logits_w = rearrange(rel_logits_w, "b (nh h) w0 w1 -> b nh h () w0 w1", nh=Nh)
        # Relative logits in height dimension next.
        rel_logits_h = relative_logits_1d(
            rearrange(x, "b nh hd (h w) -> b (nh w) hd h", h=self.h, w=self.w), self.rel_emb_h
        )
        rel_logits_h = rearrange(rel_logits_h, "b (nh w) h0 h1 -> b nh h0 h1 w ()", nh=Nh)
        return rearrange(rel_logits_h + rel_logits_w, "b nh h0 h1 w0 w1 -> b nh (h0 w0) (h1 w1)")

class AbsolutePosEmbedding(nn.Module):
    """
    Given query q of shape [batch heads tokens dim] we multiply
    q by all the flattened absolute differences between tokens.
    Learned embedding representations are shared across heads
    """

    def __init__(self, h, w, dim):
        super().__init__()
        scale = dim ** -0.5
        self.abs_pos_emb = nn.Parameter(torch.randn(h * w, dim) * scale)
        nn.init.normal_(self.abs_pos_emb, scale)

    def forward(self, x):
        """
        :param x: B Nh Hd HW
        :return: B Nh HW HW
        """
        return torch.einsum("bndx, yd -> bhxy", x, self.abs_pos_emb)

class SelfAttention2D(nn.Module):
    def __init__(self, in_dim, key_dim, value_dim, nh, hw, pos_mode="relative"):
        super(SelfAttention2D, self).__init__()
        self.dkh = key_dim // nh
        self.dvh = value_dim // nh
        self.nh = nh
        self.key_dim = key_dim
        self.value_dim = value_dim
        self.kqv_proj = nn.Conv2d(in_dim, 2 * key_dim + value_dim, 1)
        self.out_proj = nn.Conv2d(value_dim, value_dim, 1)
        if pos_mode == "relative":
            self.position_embedding = RelativePosEmbedding(h=hw[0], w=hw[1], dim=self.dkh)
        elif pos_mode == "absolute":
            self.position_embedding = AbsolutePosEmbedding(h=hw[0], w=hw[1], dim=self.dkh)
        else:
            self.position_embedding = nn.Identity()

    def split_heads_and_flatten(self, _x):
        return rearrange(_x, "b (nh hd) h w -> b nh hd (h w)", nh=self.nh)

    def forward(self, x):
        """
        :param x: B C H W
        """

        # Compute q, k, v
        k, q, v = self.kqv_proj(x).split([self.key_dim, self.key_dim, self.value_dim], dim=1)
        q = q * self.dkh ** -0.5  # scaled dot-product

        # After splitting, shape is [B, Nh, dkh or dvh, HW]
        q, k, v = map(self.split_heads_and_flatten, (q, k, v))

        # [B, Nh, HW, HW]
        logits = torch.einsum("bndx, bndy -> bnxy", q, k)
        logits += self.position_embedding(q)
        weights = logits.softmax(-1)
        attn_out = torch.einsum("bnxy, bndy -> bndx", weights, v)
        attn_out = rearrange(attn_out, "b nd hd (h w) -> b (nd hd) h w", h=x.shape[2], w=x.shape[3])

        # Project heads
        attn_out = self.out_proj(attn_out)
        return attn_out

class AugmentedConv2d(nn.Module):
    def __init__(self, in_dim, out_dim, kernel_size, key_dim, value_dim, num_heads, hw, pos_mode):
        super(AugmentedConv2d, self).__init__()
        self.std_conv = nn.Conv2d(in_dim, out_dim - value_dim, kernel_size, padding=kernel_size // 2)
        self.attention = SelfAttention2D(
            in_dim, key_dim=key_dim, value_dim=value_dim, nh=num_heads, hw=hw, pos_mode=pos_mode
        )

    def forward(self, x):
        conv_out = self.std_conv(x)
        attn_out = self.attention(x)
        return torch.cat([conv_out, attn_out], dim=1)

if __name__ == "__main__":
    m = AugmentedConv2d(
        in_dim=4, out_dim=64, kernel_size=3, key_dim=32, value_dim=48, num_heads=2, hw=(10, 10), pos_mode="relative"
    )
    print(m(torch.randn(4, 4, 10, 10)).shape)

一些疑惑

  • permutation equivariance(置换等变性), translation equivariance(平移等变性)二者的差异是什么?

补充知识

对于self-attention包含三个输入, query Q/key K/value V, 三者具体表示的含义是什么呢? 以下内容摘自https://www.cnblogs.com/rosyYY/p/10115424.html:

  1. Q、K、V中包含的都是原始数据的嵌入表示
  2. Q为什么叫query？
    1. 是因为每次需要拿一个嵌入表示去"查询"其和任意的嵌入表示之间的match程度, 也就是attention大小
  3. K和V表示键值, 关于这里的解释, 各处都语焉不详, 在 从Seq2seq到Attention模型到Self Attention(二) - 量化投资机器学习的文章 - 知乎 https://zhuanlan.zhihu.com/p/47470866 中有处提到:"key、value的起源论文 Key-Value Memory Networks for Directly Reading Documents. 在NLP的领域中, Key, Value通常就是指向同一个文字隐向量(word embedding vector)". 暂且做过多解释.

相关链接

posted @ 2021-06-07 17:24  lart  阅读(841)  评论(0)  编辑  收藏  举报