Top Tree 相关

本文只是个人学习笔记，没怎么考虑可读性，不适合学习使用。

如需学习，建议参考这篇文章。我的就是借鉴（抄袭）他的。

介绍

Top Tree 是处理一些树上（特殊图）问题的有利工具，但 Top Tree 应用场景比较少显得不是很有用，甚至一些可以用 Top Tree 解决的问题 Top Tree 相比其它解决方式常数会大很多且码量巨大，但是一些特定场景还是得用 Top Tree。

Top Tree 有静态 Top Tree 还有动态 Top Tree。

静态 Top Tree

簇是 Top Tree 的基础，一个簇可以用 \((u,v,S)\) 表示， \(u,v\) 为该簇的两个界点，\(S\) 为该簇的结点集合。

一个簇可以由两个簇合并而成，合并方式有 \(\text{compress}\) 和 \(\text{rake}\)：

• \(\text{compress}\)，是将两个簇 \((u,v,S_1)\) 和 \((v,w,S_2)\) 合并成 \((u,w,S_1 \cup S_2)\)。
• \(\text{rake}\)，是将两个簇 \((u,v,S_1)\) 和 \((v,w,S_2)\) 合并成 \((u,v,S_1 \cup S_2)\)。

除了被合并成的簇还有基簇，基簇代表一条边 \((u,v)\)，用 \((u,v,\{u,v\})\) 表示。簇中的 \(u,v\) 表示界点。两个簇合并之后会有一个界点被去掉，这个界点叫做中心点。

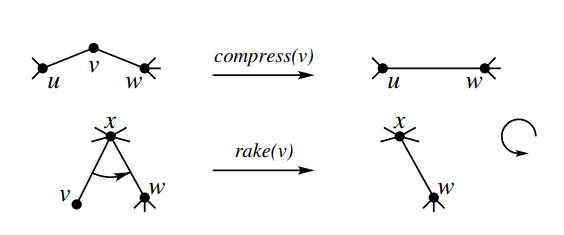
通过 \(\text{compress}\) 和 \(\text{rake}\) 操作可以将整个树的边合并成一个二叉树。

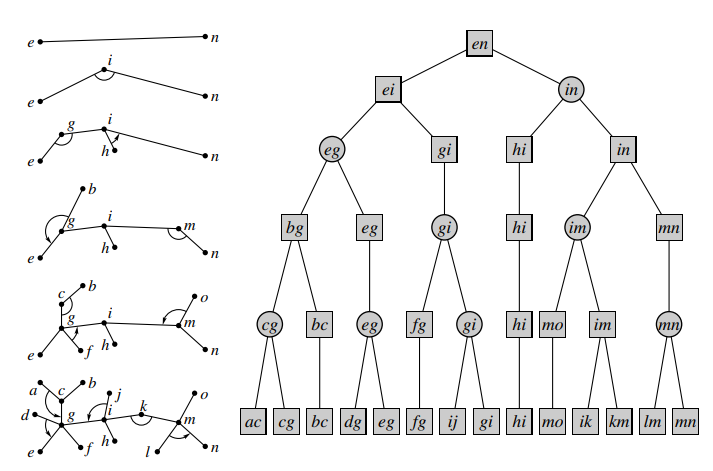
树链剖分构造方式

首先进行树练剖分，对于亲边的子树先建出它的 Top Tree，再将一个点的所有轻边的子树按照二叉树的方式合并起来，然后将一条重链上的点也按照线段树的方式合并起来。树高为 \(O(log^2n)\)。

全局平衡二叉树

全局平衡二叉树相当于树链剖分的进化版？树链剖分是对每个重链建一颗线段树，但是这个线段树不优秀，因为轻儿子的线段树会挂在当前重链线段树的叶子上，可以先挂在叶子上，然后按照重量平衡找到一个位置把左右分开成两个区间。这样树高就是 \(O(\log n)\) 的了。

静态 Top Tree 构造方式也类似。

一些操作

链上的操作：考虑一个簇只关心界点路径上的边，直接在每个重链上的线段树二分出对应线段即可。

子树的边的操作：考虑 \(u\) 所在的重链的线段树，直接在这颗线段树找到对应后缀即可。

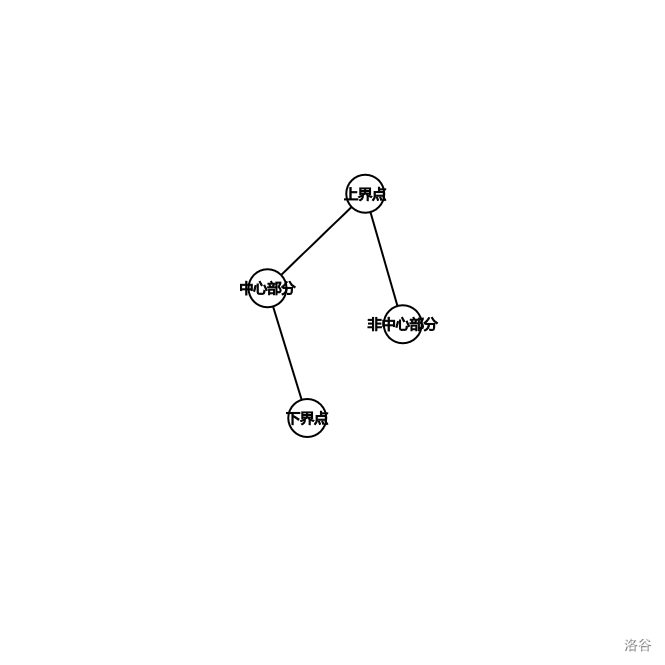
距离相关的操作：通过上文的合并方式，可以发现一个簇包含的边中连接下界点的边只有一个，而上界点就有多个，通常一个簇需要考虑三个值：簇内点和下界点距离关系，中心部分的点和上界点的距离关系，非中心部分和上界点的距离关系。中心部分：

树分块

dfs 维护栈，如果满足一下情况就把当前节点设置成界点：

• 当前子树在栈中点数量大于 \(B\)。
• 当前点至少有两个子树里面有界点。
• 根节点。

结果会导致界点数量为 \(O(B)\)。只保留界点就会建出一个收缩树。维护距离只用考虑界点即可，通过这样操作，每个点最多有两个界点与之相关。

广义串并联图上的 Top Tree

广义串并联图可以用去一度点，缩二度点，删重边的方式将图缩成一个点。去一度点和缩二度点都可以用 \(\text{compress}\) 和 \(\text{rake}\) 进行操作。但删重边就需要一个新的操作 \(\text{twist}\)，其实就是把 \((u,v,S_1)\) 和 \((u,v,S_2)\) 合并成 \((u, v, S_1\cup S_2)\)。

但是建出来的 Top Tree 明显无法保证树高。

Top Tree 的 Top Tree

在广义串并联图上 DDP，如果直接在 Top Tree 复杂度无法保证，但可以在 Top Tree 上 DDP，也就是说建出 Top Tree 的 Top Tree 或全局平衡二叉树。