傅里叶变换学习笔记

多项式乘法与卷积

在小学的时候，我们学习过两个整数如何计算他们的乘积。上了初中以后，我们又学习了如何计算两个多项式相乘。现在，让我们回顾一下这个过程，设有两个多项式 \(F_1(x) = 3 + 5x + 6x^2\)、\(F_2(x) = 9 + 7x + 11x^2 + 114514 x^3\)，则乘积的结果 \(F_3(x)\)：

\[\begin{aligned} F_3(x) = (F_1 \cdot F_2)(x)&=(3 + 5x + 6x^2) \times (9 + 7x + 11x^2 + 114514 x^3)\\ &= 27+21x+33x^2+343542x^3+45x+35x^2+55x^3+572570x^4+54x^2+42x^3+66x^4+687084x^5\\ &= 27 + 66x + 122x^2 +343639x^3+572636x^4+687084x^5 \end{aligned} \]

好，现在让我们换一个视角来看待这个问题，让我们将 \(F_1(x)\) 、\(F_2(x)\) 和 \(F_3(x)\) 系数提取出来，并记为 \(\vec c_{F_1}\)、\(\vec c_{F_2}\) 和 \(\vec c_{F_3}\)，则：

\[\begin{aligned} &\vec c_{F_1} = [3\quad5\quad6]\\ &\vec c_{F_2} = [9\quad7\quad11\quad114514]\\ &\vec c_{F_3} = [27\quad66\quad122\quad343639\quad572636\quad687084] \end{aligned} \]

现在，不妨让我们用 \(0\) 补齐 \(\vec c_{F_1}\)，则得到：

\[\begin{aligned} &\vec c_{F_1} = [3\quad5\quad6\quad0]\\ &\vec c_{F_2} = [9\quad7\quad11\quad114514]\\ &\vec c_{F_3} = [27\quad66\quad122\quad343639\quad572636\quad687084] \end{aligned} \]

让我们运用 \(\color{black}{\mathbf{O}}\color{red}{\text{Ier}}\) 的智慧来观察 \(\vec c_{F_1}\)、\(\vec c_{F_2}\) 和 \(\vec c_{F_3}\) 的规律，发现 \(\vec c_{F_3}\) 本质上就是 \(\vec c_{F_2}\) 翻转，然后以一个类似于滑动窗口的方式与 \(\vec c_{F_1}\) 相乘，然后将得到的结果去 \(0\)。可能这么说比较抽象，我们不妨用一个更加形式化的方法来描述这一过程：

\[\vec c_{F_3}\,[n] = \sum_{i=0}^{\operatorname{size}(\vec c_{F_1})} \vec c_{F_1}\,[i] \cdot \vec c_{F_2}\,[n-i] \]

好，让我们现在给这一个美妙的操作起一个比较高大上的名字，叫做「卷积（Convolution）」，我们发现，任意两个多项式相乘的本质上都是对其系数进行卷积操作后得到的结果。

当然，目前所讲的卷积属于离散卷积，其标准定义为：给定两个离散信号 \(f(x)\) 和 \(g(x)\)，然后定义 \(s(x) = (f \cdot g)(x)\) 为：

\[s(x) = (f\cdot g) (x) = \sum_{i=-\infty} ^ {\infty} f(i) \cdot g(x - i) \]

通过离散卷积的标准定义，我们也不难发现，离散卷积本质上就是定义了两个离散函数应当如何实现「乘法」这一操作。

我们不难发现，如果让我们直接计算两个多项式的卷积的话，我们将会得到一个 \(\mathcal O(n^2)\) 复杂度的算法，现在我们有没有什么更加优秀的算法让我们能进一步优化复杂度呢？这就需要聊聊：

傅里叶变换

现在让我们运用一下初中学到的知识，考虑我们想要在平面直角坐标系上确定一条直线，应该需要至少几个点？显然，根据初中几何告诉我们的一条定理「两点确定一条直线」可以知道我们至少需要两个点才能确定一条直线。

我们不妨用解析几何的语言来重新描述一下上方命题，即「给定两个 \(x\) 值不同的点，能且仅能确定一个一次函数」。当然，我们也可以将上述命题扩展一下，即得到命题「给定 \(N\) 个待求 \(N-1\) 次函数上的 \(x\) 值不同的点，能且仅能确定一个 \(N-1\) 次函数」。证明如下：

本质上来说，我们用 \(N\) 个 \(x\) 值互不相同的点来确定 \(N-1\) 次函数的过程本质上就是用一个 \(N\) 项的线性方程组来确定 \(N-1\) 次函数每一项的系数，得到的形式如下：

\[\begin{cases} c_0+c_1x_0+c_2x^2_0+c_3x_0^3+ \cdots +c_{n-2}x_0^{n-2}+c_{n-1}x_0^{n-1} = F(x_0)\\ c_0+c_1x_1+c_2x_1^2+c_3x_1^3+ \cdots +c_{n-2}x_1^{n-2}+c_{n-1}x_1^{n-1} = F(x_1)\\ c_0+c_1x_2+c_2x_2^2+c_3x_2^3+ \cdots +c_{n-2}x_2^{n-2}+c_{n-1}x_2^{n-1} = F(x_2)\\ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ \vdots\\ c_0+c_1x_n+c_2x_n^2+c_3x_n^3+ \cdots +c_{n-2}x_n^{n-2}+c_{n-1}x_n^{n-1} = F(x_n)\\ \end{cases} \]

首先证明方程组不会出现无解的情况，这一点是根据我们的命题得出的。故可以得出此时方程组必然存在至少一个解，即对于任意两个方程 \(A\)、\(B\) 之间，我们都有 \(c_{Ai} = c_{Bi}\) 相等。
然后，对于这个线性方程组，我们可以证明上述方程有且仅有一个解，证明如下：
现有待拟合 \(n-1\) 次多项式，则显然有 \(c_{n-1} \not= 0\)，假设 \(A = pB\quad(p\in \mathbb{R})\)，则有 \(c_{An-1}x_A^n = pc_{Bn-1}x_B^n\)，因为 \(A\)、\(B\) 两式出自同一多项式，故有 \(c_{An-1} = c_{Bn-1}\)，于是可以得到 \(x_A^n = px_B^n\)，即 \(x_A = \sqrt[n]{p}x_B\)，则有下述两种情况：

1. 多项式含有低于 \(n\) 次的项：
   则我们还有 \(c_{Am}x_A^m = pc_{Bm}x_B^m \quad(m\lt n)\)，因为 \(c_{Am} = c_{Bm}\)，则有 \(x_A^m = px_B^m\) 则 \(x_A = \sqrt[m]{p}x_B\)，则显然此时 \(x_A = x_B = 0\)，但是我们有条件「\(x\) 值互不相同」即「\(x_A \not= x_B\)」，故舍去该条件。
2. 多项式不含有低于 \(n\) 次的项：
   则此时方程组只有一个未知量，可以得出方程的解为 \(c_{n-1} = \dfrac{F(x_A)}{x_A}\)。

实际上，上述内容就是数学中的一个比较重要的概念：「插值」。

于是，我们对于求两个 \(n\) 次多项式 \(F_1(x)\) 和 \(F_2(x)\) 相乘就有了一个新的思路：

• 分别在 \(F_1(x)\) 和 \(F_2(x)\) 中 “随机” 取得相同位置 \(2n\) 个点，分别归入点集 \(A\) 和 \(B\)。
• 将点集 \(A\) 和 \(B\) 之间的纵坐标相乘，得到新的点集 \(C\)。
• 对点集 \(C\) 带入上述的方程组，求得相乘出来的多项式的系数。

看起来这个算法似乎应该是 \(\mathcal O(n^3)\) 的，因为高斯消元求解线性方程组是 \(O(n^3)\) 的，但是本质上上述内容是在进行插值，故我们可以使用拉格朗日插值法来插出原多项式，故时间复杂度还是 \(\mathcal O(n^2)\)。

但是目前和傅里叶变换好像似乎……没啥关系，确实，到目前为止我们还没有引入傅里叶变换，因为在这之前，我们需要了解一个名叫：

单位根

我相信在座的各位肯定都学过复数了。当然，没学过也不要紧，复数的出现本质上就是为了解决一元三次方程通项公式中关于「负数的平方根」这一问题的，现在让我们设 \(\text{i}^2= -1\)，并规定 \(\text{i}\) 为虚数单位，称类似于 \(a+b\text{i}\; (a,b\in \mathbb{R})\) 为复数，并定义了一下 \(\mathbb{C}\) 为复数域，然后用几何表明了复数的意义，并且规定由实轴和虚轴张成的空间叫做复平面。

根据代数基本定理，我们可以知道，\(n\) 次方程必定有且只有 \(n\) 个根（证明去问高斯）。于是对于方程 \(x^n = 1\) 我们就有了 \(n\) 个根，我们称这 \(n\) 个根为 \(n\) 次单位根。观察复平面上 \(n\) 单位根，我们会发现其将一个圆心为原点，半径为 \(1\) 的单位圆均等分为 \(n\) 了，例如下面的 \(8\) 次单位根：

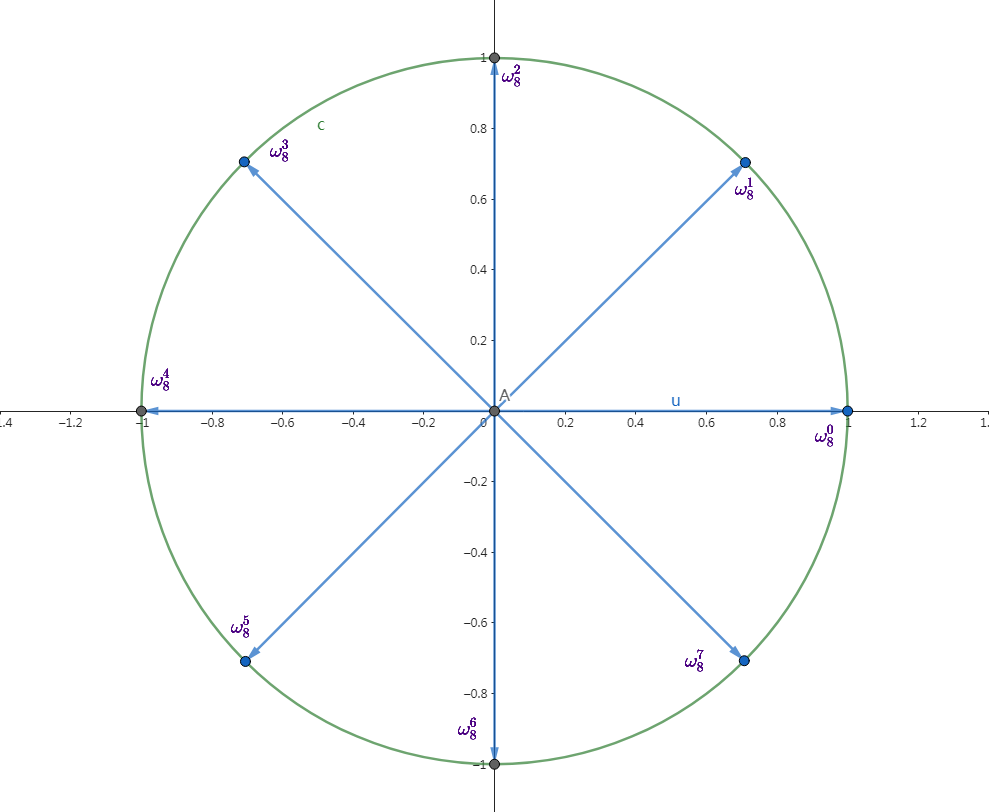
于是我们可以十分轻易的将 \(a+b\text{i}\) 形式转化为三角形式，即：

\[\omega_n^k = \cos \dfrac{2k\pi}{n} + \text{i}\sin \dfrac{2k\pi}{n} \]

再通过我们伟大的欧拉公式，能将其转化为复变函数形式：

\[\omega_n^k = e^{\text{i}\frac{2\pi}{n}k} \]

下面给出三条与单位根有关的引理：

1. 消去引理：对于任意正整数 \(n,k,d\gt 0\)，我们有 \(\omega_{dn}^{dk} = \omega_n^{k}\)

2. 折半引理：若有整数 \(n\gt 0\) 为偶数，则 \(n\) 个 \(n\) 次单位根的平方的集合是两个 \(\dfrac{n}{2}\) 个 \(\dfrac{n}{2}\) 次单位根的集合，即 \((\omega_n^k)^2 = (\omega_n^{k+\frac{n}{2}})^2 = \omega_{\frac{n}{2}}^k\)

3. 求和引理：对于任意正整数 \(n\ge 1\) 和不能被 \(n\) 整除的非负整数 \(k\)，有 \(\sum_{j=0}^{n-1} (\omega^k_n)^j = 0\)

现在，我们已经知道了单位根和求多项式乘法的另一个算法了，现在我们就开始讲：

离散傅里叶变换（DFT）

现有有限数列 \(\{c_n\}_{n=0}^{N-1}\)，则定义其「离散傅里叶变换（DFT）」为：

\[\hat c_k = \sum_{i=0}^{N-1} c_i \cdot (\omega_{N}^{k})^i \]

注：在很多 CS 的文献中，经常把 DFT 的式子写成：

\[\hat c_k = \sum_{i=0}^{N-1} c_i \cdot e^{-\text{i}\frac{2\pi}{N}ki} \]

实际上，这两者产生的效果是一样的，唯一的区别仅仅是在单位根是顺时针标号还是逆时针标号而已，不过在工程数学上，我们一般逆时针取单位根。

我们可以发现，DFT 本质上是将原先对 \(x\) 的取值从实数域 \(\mathbb{R}\) 上转移到了 \(n\) 次单位根上了，所以不难看出 \(\hat c\) 本质上就是对原多项式在 \(n\) 次单位根上的结果。

则其「逆离散傅里叶变换（IDFT）」为：

\[c_k = \frac{1}{N}\sum_{i=0}^{N-1} \hat c_i \cdot (\omega_{N}^{k})^{-i} \]