【树】二叉树的应用 II

1.【树】二叉树的应用 II2024-01-25

2.【树】二叉树的应用 I2024-01-27

1. 题目
2. 应用

1. 题目

二叉树相关的题目：

序号	题目	难度
1	124. 二叉树中的最大路径和	困难
2	100. 相同的树	简单
3	105. 从前序与中序遍历序列构造二叉树	中等
4	106. 从中序与后序遍历序列构造二叉树	中等
5	889. 根据前序和后序遍历构造二叉树	中等
6	654. 最大二叉树	中等
7	108. 将有序数组转换为二叉搜索树	简单
8	109. 有序链表转换二叉搜索树	中等

2. 应用

2.1. Leetcode 124. 二叉树中的最大路径和

2.1.1. 题目

124. 二叉树中的最大路径和

2.1.2. 解题思路

根据题意，最大路径和一定是当前节点与左右子树的对路径的贡献之和。

由于求最大路径和的时候，需要离开当前节点的时候才能得到当前节点对当前路径的贡献。因此，这里，我们需要使用后序遍历的方式求解。

我们定义一个递归函数：int dfs(TreeNode root)，用于返回当前节点对最大路径的贡献，在遍历每一个节点后，同时，更新最大路径和即可。

注意，由于节点有负值，因此，当某一个节点的贡献为负值时，需要将其去掉，即它对路径和的贡献为 $0$ 。

2.1.3. 代码实现

 class Solution {
    private int result = Integer.MIN_VALUE;
    public int maxPathSum(TreeNode root) {
        result = Integer.MIN_VALUE;
        dfs(root);
        return result;
    }
 
    private int dfs(TreeNode root) {
        if (root == null) {
            return 0;
        }
 
        int left = Math.max(dfs(root.left), 0);
        int right = Math.max(dfs(root.right), 0);
        result = Math.max(result, root.val + left + right);
        return root.val + Math.max(left, right);
    }
}

2.2. Leetcode 100. 相同的树

2.2.1. 题目

100. 相同的树

给你两棵二叉树的根节点 p 和 q ，编写一个函数来检验这两棵树是否相同。如果两个树在结构上相同，并且节点具有相同的值，则认为它们是相同的。

示例 1：

输入：p = [1,2,3], q = [1,2,3]
输出：true

2.2.2. 解题思路

同时遍历两个二叉树，在前序的位置判断节点是否相同即可。

2.2.3. 代码实现

 class Solution {
    public boolean isSameTree(TreeNode p, TreeNode q) {
        return dfs(p, q);
    }
 
    private boolean dfs(TreeNode p, TreeNode q) {
        if ((p == null && q != null) || (p != null && q == null)) {
            return false;
        }
 
        if (p == null && q == null) {
            return true;
        }
 
        if (p.val != q.val) {
            return false;
        }
 
        return dfs(p.left, q.left) && dfs(p.right, q.right);
    }
}

2.3. Leetcode 105. 从前序与中序遍历序列构造二叉树

2.3.1. 题目

105. 从前序与中序遍历序列构造二叉树

给定两个整数数组 preorder 和 inorder ，其中 preorder 是二叉树的先序遍历， inorder 是同一棵树的中序遍历，请构造二叉树并返回其根节点。

示例 1：

输入: preorder = [3,9,20,15,7], inorder = [9,3,15,20,7]
输出: [3,9,20,null,null,15,7]

2.3.2. 解题思路

2.3.2.1. 找到根节点

前序遍历有一个很重要的性质：前序遍历数组中的第一个节点就是根节点。

2.3.2.2. 找到左子树和右子树

利用前序数组找到根节点后，我们可以通过这个节点，在中序数组中，将其划分为两个子数组，这样，就得到了左右子树的长度，这样，即可将前序数组分成两部分，继续递归建树。

这里，我们利用了分治的思想，根节点两侧的每一个子树都满足：前序遍历数组中的第一个元素是根节点，该节点在中序遍历数组中的左侧所有元素都是该节点的左子树，它的右侧所有元素都是它的右子树。

所以，可以将前序遍历数组拆分为左右子树，分别递归计算当前节点的左右子树。

2.3.3. 代码实现

 class Solution {
    public TreeNode buildTree(int[] preorder, int[] inorder) {
        int n = preorder.length;
        Map<Integer, Integer> index = new HashMap<>();
        for (int i = 0; i < inorder.length; i++) {
            index.put(inorder[i], i);
        }
        return dfs(preorder, index, 0, n - 1, 0, n - 1);
    }
 
    private TreeNode dfs(int[] preorder, Map<Integer, Integer> index, 
                         int preorderLeft, int preorderRight, int inorderLeft, int inorderRight) {
        if (preorderLeft > preorderRight) {
            return null;
        }
        int pivot = preorder[preorderLeft];
        int pivotIndex = index.get(pivot);
        TreeNode root = new TreeNode(pivot);
        // 左子树的长度
        int leftSubtreeSize = pivotIndex - inorderLeft;
        root.left = dfs(preorder, index, preorderLeft + 1, preorderLeft + leftSubtreeSize, inorderLeft, pivotIndex - 1);
        root.right = dfs(preorder, index, preorderLeft + leftSubtreeSize + 1, preorderRight, pivotIndex + 1, inorderRight);
        return root;
    }
}

类似的题目有：

1008. 前序遍历构造二叉搜索树

2.4. Leetcode 106. 从中序与后序遍历序列构造二叉树

2.4.1. 题目

106. 从中序与后序遍历序列构造二叉树

给定两个整数数组 inorder 和 postorder ，其中 inorder 是二叉树的中序遍历， postorder 是同一棵树的后序遍历，请你构造并返回这颗二叉树。

示例 1：

输入：inorder = [9,3,15,20,7], postorder = [9,15,7,20,3]
输出：[3,9,20,null,null,15,7]

2.4.2. 解题思路

2.4.2.1. 找到根节点

后序遍历有一个很重要的性质：后序遍历数组中的最后一个节点就是根节点。

2.4.2.2. 找到左子树和右子树

利用后序数组找到根节点后，我们可以通过这个节点，在中序数组中，将其划分为两个子数组，这样，就得到了左右子树的长度，这样，即可将后序数组分成两部分，继续递归建树。

这里，我们利用了分治的思想，根节点两侧的每一个子树都满足：后序遍历数组中的第一个元素是根节点，该节点在中序遍历数组中的左侧所有元素都是该节点的左子树，它的右侧所有元素都是它的右子树。

所以，可以将后序遍历数组拆分为左右子树，分别递归计算当前节点的左右子树。

2.4.3. 代码实现

 class Solution {
    public TreeNode buildTree(int[] inorder, int[] postorder) {
        Map<Integer, Integer> index = new HashMap<>();
        int n = inorder.length;
        for (int i = 0; i < n; i++) {
            index.put(inorder[i], i);
        }
        return dfs(postorder, index, 0, n - 1, 0, n - 1);
    }
 
    private TreeNode dfs(int[] postorder, Map<Integer, Integer> index, int inLeft, int inRight, int postLeft, int postRight) {
        if (postLeft > postRight) {
            return null;
        }
 
        int pivot = postorder[postRight];
        int pivotIndex = index.get(pivot);
 
        TreeNode root = new TreeNode(pivot);
 
        int leftSubtreeSize = pivotIndex - inLeft;
        root.left = dfs(postorder, index, inLeft, pivotIndex - 1, postLeft, postLeft + leftSubtreeSize - 1);
        root.right = dfs(postorder, index, pivotIndex + 1, inRight, postLeft + leftSubtreeSize, postRight - 1);
        return root;
    }
}

2.5. Leetcode 889. 根据前序和后序遍历构造二叉树

2.5.1. 题目

889. 根据前序和后序遍历构造二叉树

给定两个整数数组，preorder 和 postorder ，其中 preorder 是一个具有无重复值的二叉树的前序遍历，postorder 是同一棵树的后序遍历，重构并返回二叉树。
如果存在多个答案，您可以返回其中任何一个。

示例 1：

输入：preorder = [1,2,4,5,3,6,7], postorder = [4,5,2,6,7,3,1]
输出：[1,2,3,4,5,6,7]

2.5.2. 解题思路

解题思路：

将前序遍历数组的第一个元素作为根节点；
把前序遍历数组中的第二元素作为左子树的根节点；
在后序遍历数组中，找到左子树的根节点的位置，这样就可以确定左子树的长度，进而就确定了右子树的长度，然后，递归建树即可；

注意：这里，我们假设前序遍历的数组最少有两个节点，如果它只有一个节点时，需要特殊处理，因此，这种情况下，我们直接返回一个新的二叉树节点即可。

2.5.3. 代码实现

 class Solution {
    public TreeNode constructFromPrePost(int[] preorder, int[] postorder) {
        Map<Integer, Integer> index = new HashMap<>();
        int n = postorder.length;
        for (int i = 0; i < n; i++) {
            index.put(postorder[i], i);
        }
 
        return dfs(preorder, postorder, index, 0, n - 1, 0, n - 1);
    }
 
    private TreeNode dfs(int[] preorder, int[] postorder, Map<Integer, Integer> index, 
                         int preLeft, int preRight, int postLeft, int postRight) {
        if (preLeft > preRight) {
            return null;
        }
        // 当区间长度为 1 时，直接返回一个新节点
        if (preLeft == preRight) {
            return new TreeNode(preorder[preLeft]);
        }
        // 当前的根节点
        int pivot = preorder[preLeft];
        TreeNode root = new TreeNode(pivot);
        // 左子树的根节点
        int leftSubRoot = preorder[preLeft + 1];
        int leftRootIndex = index.get(leftSubRoot);
        int leftSubtreeSize = leftRootIndex - postLeft + 1;
 
        root.left = dfs(preorder, postorder, index,
                preLeft + 1, preLeft + leftSubtreeSize, postLeft, leftRootIndex);
        root.right = dfs(preorder, postorder, index, 
                preLeft + leftSubtreeSize + 1, preRight, leftRootIndex + 1, postRight - 1);
        return root;
    }
}

2.6. Leetcode 654. 最大二叉树

2.6.1. 题目

654. 最大二叉树

给定一个不重复的整数数组 nums 。 最大二叉树 可以用下面的算法从 nums 递归地构建:

创建一个根节点，其值为 nums 中的最大值。

递归地在最大值左边的 子数组前缀上 构建左子树。

递归地在最大值右边的 子数组后缀上 构建右子树。

返回 nums 构建的 最大二叉树 。

示例 1：

输入：nums = [3,2,1,6,0,5]
输出：[6,3,5,null,2,0,null,null,1]
解释：递归调用如下所示：

[3,2,1,6,0,5] 中的最大值是 6 ，左边部分是 [3,2,1] ，右边部分是 [0,5] 。

[3,2,1] 中的最大值是 3 ，左边部分是 [] ，右边部分是 [2,1] 。

空数组，无子节点。

[2,1] 中的最大值是 2 ，左边部分是 [] ，右边部分是 [1] 。

空数组，无子节点。

只有一个元素，所以子节点是一个值为 1 的节点。

[0,5] 中的最大值是 5 ，左边部分是 [0] ，右边部分是 [] 。

只有一个元素，所以子节点是一个值为 0 的节点。

空数组，无子节点。

提示：

1 <= nums.length <= 1000

0 <= nums[i] <= 1000

nums 中的所有整数互不相同

2.6.2. 解题思路

题目的要求是建树，这里我们定义一个递归函数，用于返回当前节点的子树。

算法思路：

在前序的位置创建节点，构造节点前，先从子数组中找到最大的元素，作为当前节点的值；
在后序的位置连接当前节点的左右子树。

2.6.3. 代码实现

 class Solution {
    public TreeNode constructMaximumBinaryTree(int[] nums) {
        return dfs(nums, 0, nums.length - 1);
    }
 
    private TreeNode dfs(int [] nums, int left, int right) {
        if (left > right) {
            return null;
        }
 
        int i = maxIndex(nums, left, right);
        TreeNode root = new TreeNode(nums[i]);
        root.left = dfs(nums, left, i -1);
        root.right = dfs(nums, i + 1, right);
        return root;
    }
 
    private int maxIndex(int [] nums, int left, int right) {
        int result = left;
        for (int i = left + 1; i <= right; i++) {
            if (nums[result] < nums[i]) {
                result = i;
            }
        }
        return result;
    }
}

2.7. Leetcode 108. 将有序数组转换为二叉搜索树

2.7.1. 题目

108. 将有序数组转换为二叉搜索树

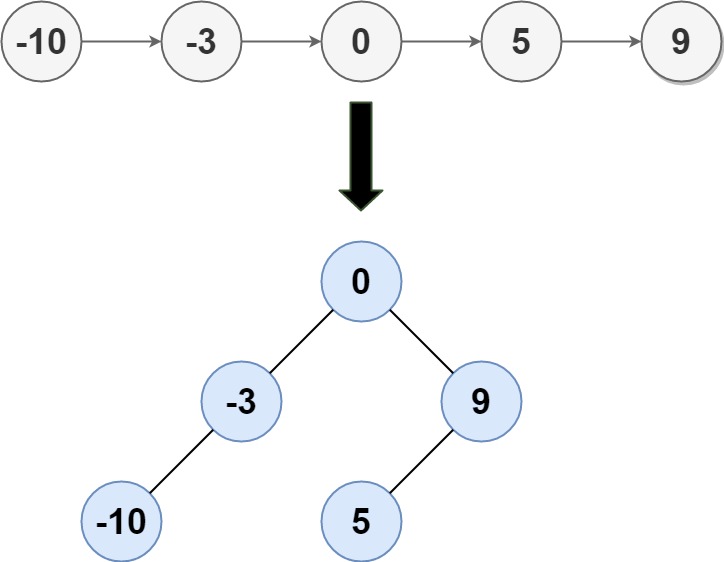
给你一个整数数组 nums ，其中元素已经按升序排列，请你将其转换为一棵平衡二叉搜索树。

示例 1：

输入：nums = [-10,-3,0,5,9]
输出：[0,-3,9,-10,null,5]
解释：[0,-10,5,null,-3,null,9] 也将被视为正确答案：

提示：

$1 <= n u m s . l e n g t h <= 10^{4}$

$- 10^{4} <= n u m s [i] <= 10^{4}$

nums 按 严格递增 顺序排列

2.7.2. 解题思路

二叉搜索树：对任意一个节点，左子树上所有节点的值均小于它的根节点，右子树上所有节点的值均大于它的根节点的值。

这样，二叉搜索树的中序遍历一定是升序序列。

为了简单起见，每次创建节点时，均选择数组子区间的中点作为根节点，递归创建即可。

2.7.3. 代码实现

 class Solution {
    public TreeNode sortedArrayToBST(int[] nums) {
        return dfs(nums, 0, nums.length - 1);
    }
 
    private TreeNode dfs(int [] nums, int left, int right) {
        if (left > right) {
            return null;
        }
        int mid = left + (right - left) / 2;
        TreeNode root = new TreeNode(nums[mid]);
        root.left = dfs(nums, left, mid - 1);
        root.right = dfs(nums, mid + 1, right);
        return root;
    }
}

2.8. Leetcode 109. 有序链表转换二叉搜索树

2.8.1. 题目

109. 有序链表转换二叉搜索树

给定一个单链表的头节点 head ，其中的元素按升序排序，将其转换为平衡二叉搜索树。

示例 1：

输入: head = [-10,-3,0,5,9]
输出: [0,-3,9,-10,null,5]
解释: 一个可能的答案是 [0，-3,9，-10,null,5]，它表示所示的高度平衡的二叉搜索树。

提示：

head 中的节点数在 $[0, 2 * 10^{4}]$ 范围内

$- 10^{5} <= N o d e . v a l <= 10^{5}$

2.8.2. 解题思路

2.8.2.1. 方法一：分治

题目要求，平衡二叉树的左右子树的高度之差不超过 1，比较直观的做法是：让左右子树的节点个数尽可能相等。

那么，我们就可以通过分治的思想，每次取链表的中位数，作为根节点，递归建树即可。

求链表的中位数，可以采用快慢指针的方法，即每次快指针移动两步，慢指针移动一步。

2.8.2.2. 方法二：分治 + 中序遍历

BST 的中序遍历，就是一个升序序列，所以，可以利用中序遍历的性质建树，即：一边中序遍历的方式建树，同时，顺序遍历链表。

由于 BST 的左右子树高度差不超过 $1$ ，所以，每次搜索的时候，直接以数组元素下标的区间作为递归条件。

起始的搜索区间是一个闭区间: $[0, n - 1]$ ， $l e f t$ 最多取到 $n - 1$ ，不可能大于 $n - 1$ ，所以递归的结束条件是： $l e f t > r i g h t$ 。

2.8.3. 代码实现

2.8.4.1. 方法一

 class Solution {
    public TreeNode sortedListToBST(ListNode head) {
        return dfs(head, null);
    }
 
    private TreeNode dfs(ListNode left, ListNode right) {
        if (left == right) {
            return null;
        }
        // 在前序的位置创建节点，在后序的位置连接左右子树
        ListNode midNode = getMidNode(left, right);
        TreeNode root = new TreeNode(midNode.val);
        root.left = dfs(left, midNode);
        root.right = dfs(midNode.next, right);
        return root;
    }
 
    private ListNode getMidNode(ListNode left, ListNode right) {
        ListNode slow = left, fast = left;
        while (fast != right && fast.next != right) {
            slow = slow.next;
            fast = fast.next.next;
        }
        return slow;
    }
}

复杂度：

时间复杂度： $O (n l o g_{2} n)$

遍历完链表中的 $n$ 个节点，需要的时间复杂度为 $O (n)$ 。

同时，对于链表的每一个子区间计算中点的过程，都是折半查找的过程，设查找的次数为 $k$ ，则 $1 = \frac{n}{2^{k}}$ ，因此，查找的次数 $k = l o g_{2} n$ 。

因此，总的时间复杂度为 $O (n l o g_{2} n)$ 。
空间复杂度： $O (l o g_{2} n)$

空间复杂度为栈的最大深度，即二叉树的最大高度，平衡二叉树的最大高度不超过 $O (l o g_{2} n)$ 。

2.8.4.2. 方法二

 class Solution {
    // 为了保证进入某个节点和离开某个节点时，访问的是链表中的同一个元素
    private ListNode p;
 
    public TreeNode sortedListToBST(ListNode head) {
        int n = getListLength(head);
        p = head;
        return dfs(0, n - 1);
    }
 
    private TreeNode dfs(int left, int right) {
        if (left > right) {
            return null;
        }
        // 在前序位置创建一个新节点
        int mid = left + (right - left) / 2;
        TreeNode root = new TreeNode();
        root.left = dfs(left, mid - 1);
        // 在中序位置赋值，并遍历链表
        root.val = p.val;
        p = p.next;
        root.right = dfs(mid + 1, right);
        return root;
    }
 
    private int getListLength(ListNode head) {
        int length = 0;
        while (head != null) {
            length++;
            head = head.next;
        }
        return length;
    }
}

复杂度：

时间复杂度： $O (n)$
空间复杂度： $O (l o g_{2} n)$

参考：

东哥手把手带你刷二叉树（构造篇）

本文作者：LARRY1024

本文链接：https://www.cnblogs.com/larry1024/p/17988000

posted @ 2024-01-25 19:41 LARRY1024 阅读(18) 评论(0) 编辑收藏举报

刷新页面返回顶部

登录后才能查看或发表评论，立即登录或者逛逛博客园首页

公告

昵称：LARRY1024 园龄：11年9个月粉丝：16 关注：3

昵称： LARRY1024
园龄： 11年9个月
粉丝： 16
关注： 3

+加关注

Talk is cheap, show|

2025年3月

日

一

二

三

四

五

六

	class Solution {
	private int result = Integer.MIN_VALUE;
	public int maxPathSum(TreeNode root) {
	result = Integer.MIN_VALUE;
	dfs(root);
	return result;
	}

	private int dfs(TreeNode root) {
	if (root == null) {
	return 0;
	}

	int left = Math.max(dfs(root.left), 0);
	int right = Math.max(dfs(root.right), 0);
	result = Math.max(result, root.val + left + right);
	return root.val + Math.max(left, right);
	}
	}

	class Solution {
	public boolean isSameTree(TreeNode p, TreeNode q) {
	return dfs(p, q);
	}

	private boolean dfs(TreeNode p, TreeNode q) {
	if ((p == null && q != null) \|\| (p != null && q == null)) {
	return false;
	}

	if (p == null && q == null) {
	return true;
	}

	if (p.val != q.val) {
	return false;
	}

	return dfs(p.left, q.left) && dfs(p.right, q.right);
	}
	}

	class Solution {
	public TreeNode buildTree(int[] preorder, int[] inorder) {
	int n = preorder.length;
	Map<Integer, Integer> index = new HashMap<>();
	for (int i = 0; i < inorder.length; i++) {
	index.put(inorder[i], i);
	}
	return dfs(preorder, index, 0, n - 1, 0, n - 1);
	}

	private TreeNode dfs(int[] preorder, Map<Integer, Integer> index,
	int preorderLeft, int preorderRight, int inorderLeft, int inorderRight) {
	if (preorderLeft > preorderRight) {
	return null;
	}
	int pivot = preorder[preorderLeft];
	int pivotIndex = index.get(pivot);
	TreeNode root = new TreeNode(pivot);
	// 左子树的长度
	int leftSubtreeSize = pivotIndex - inorderLeft;
	root.left = dfs(preorder, index, preorderLeft + 1, preorderLeft + leftSubtreeSize, inorderLeft, pivotIndex - 1);
	root.right = dfs(preorder, index, preorderLeft + leftSubtreeSize + 1, preorderRight, pivotIndex + 1, inorderRight);
	return root;
	}
	}

	class Solution {
	public TreeNode buildTree(int[] inorder, int[] postorder) {
	Map<Integer, Integer> index = new HashMap<>();
	int n = inorder.length;
	for (int i = 0; i < n; i++) {
	index.put(inorder[i], i);
	}
	return dfs(postorder, index, 0, n - 1, 0, n - 1);
	}

	private TreeNode dfs(int[] postorder, Map<Integer, Integer> index, int inLeft, int inRight, int postLeft, int postRight) {
	if (postLeft > postRight) {
	return null;
	}

	int pivot = postorder[postRight];
	int pivotIndex = index.get(pivot);

	TreeNode root = new TreeNode(pivot);

	int leftSubtreeSize = pivotIndex - inLeft;
	root.left = dfs(postorder, index, inLeft, pivotIndex - 1, postLeft, postLeft + leftSubtreeSize - 1);
	root.right = dfs(postorder, index, pivotIndex + 1, inRight, postLeft + leftSubtreeSize, postRight - 1);
	return root;
	}
	}

	class Solution {
	public TreeNode constructFromPrePost(int[] preorder, int[] postorder) {
	Map<Integer, Integer> index = new HashMap<>();
	int n = postorder.length;
	for (int i = 0; i < n; i++) {
	index.put(postorder[i], i);
	}

	return dfs(preorder, postorder, index, 0, n - 1, 0, n - 1);
	}

	private TreeNode dfs(int[] preorder, int[] postorder, Map<Integer, Integer> index,
	int preLeft, int preRight, int postLeft, int postRight) {
	if (preLeft > preRight) {
	return null;
	}
	// 当区间长度为 1 时，直接返回一个新节点
	if (preLeft == preRight) {
	return new TreeNode(preorder[preLeft]);
	}
	// 当前的根节点
	int pivot = preorder[preLeft];
	TreeNode root = new TreeNode(pivot);
	// 左子树的根节点
	int leftSubRoot = preorder[preLeft + 1];
	int leftRootIndex = index.get(leftSubRoot);
	int leftSubtreeSize = leftRootIndex - postLeft + 1;

	root.left = dfs(preorder, postorder, index,
	preLeft + 1, preLeft + leftSubtreeSize, postLeft, leftRootIndex);
	root.right = dfs(preorder, postorder, index,
	preLeft + leftSubtreeSize + 1, preRight, leftRootIndex + 1, postRight - 1);
	return root;
	}
	}

	class Solution {
	public TreeNode constructMaximumBinaryTree(int[] nums) {
	return dfs(nums, 0, nums.length - 1);
	}

	private TreeNode dfs(int [] nums, int left, int right) {
	if (left > right) {
	return null;
	}

	int i = maxIndex(nums, left, right);
	TreeNode root = new TreeNode(nums[i]);
	root.left = dfs(nums, left, i -1);
	root.right = dfs(nums, i + 1, right);
	return root;
	}

	private int maxIndex(int [] nums, int left, int right) {
	int result = left;
	for (int i = left + 1; i <= right; i++) {
	if (nums[result] < nums[i]) {
	result = i;
	}
	}
	return result;
	}
	}

	class Solution {
	public TreeNode sortedArrayToBST(int[] nums) {
	return dfs(nums, 0, nums.length - 1);
	}

	private TreeNode dfs(int [] nums, int left, int right) {
	if (left > right) {
	return null;
	}
	int mid = left + (right - left) / 2;
	TreeNode root = new TreeNode(nums[mid]);
	root.left = dfs(nums, left, mid - 1);
	root.right = dfs(nums, mid + 1, right);
	return root;
	}
	}

	class Solution {
	public TreeNode sortedListToBST(ListNode head) {
	return dfs(head, null);
	}

	private TreeNode dfs(ListNode left, ListNode right) {
	if (left == right) {
	return null;
	}
	// 在前序的位置创建节点，在后序的位置连接左右子树
	ListNode midNode = getMidNode(left, right);
	TreeNode root = new TreeNode(midNode.val);
	root.left = dfs(left, midNode);
	root.right = dfs(midNode.next, right);
	return root;
	}

	private ListNode getMidNode(ListNode left, ListNode right) {
	ListNode slow = left, fast = left;
	while (fast != right && fast.next != right) {
	slow = slow.next;
	fast = fast.next.next;
	}
	return slow;
	}
	}

	class Solution {
	// 为了保证进入某个节点和离开某个节点时，访问的是链表中的同一个元素
	private ListNode p;

	public TreeNode sortedListToBST(ListNode head) {
	int n = getListLength(head);
	p = head;
	return dfs(0, n - 1);
	}

	private TreeNode dfs(int left, int right) {
	if (left > right) {
	return null;
	}
	// 在前序位置创建一个新节点
	int mid = left + (right - left) / 2;
	TreeNode root = new TreeNode();
	root.left = dfs(left, mid - 1);
	// 在中序位置赋值，并遍历链表
	root.val = p.val;
	p = p.next;
	root.right = dfs(mid + 1, right);
	return root;
	}

	private int getListLength(ListNode head) {
	int length = 0;
	while (head != null) {
	length++;
	head = head.next;
	}
	return length;
	}
	}

LARRY1024

【树】二叉树的应用 II

1. 题目

2. 应用

2.1. Leetcode 124. 二叉树中的最大路径和

2.1.1. 题目

2.1.2. 解题思路

2.1.3. 代码实现

2.2. Leetcode 100. 相同的树

2.2.1. 题目

2.2.2. 解题思路

2.2.3. 代码实现

2.3. Leetcode 105. 从前序与中序遍历序列构造二叉树

2.3.1. 题目

2.3.2. 解题思路

2.3.2.1. 找到根节点

2.3.2.2. 找到左子树和右子树

2.3.3. 代码实现

2.4. Leetcode 106. 从中序与后序遍历序列构造二叉树

2.4.1. 题目

2.4.2. 解题思路

2.4.2.1. 找到根节点

2.4.2.2. 找到左子树和右子树

2.4.3. 代码实现

2.5. Leetcode 889. 根据前序和后序遍历构造二叉树

2.5.1. 题目

2.5.2. 解题思路

2.5.3. 代码实现

2.6. Leetcode 654. 最大二叉树

2.6.1. 题目

2.6.2. 解题思路

2.6.3. 代码实现

2.7. Leetcode 108. 将有序数组转换为二叉搜索树

2.7.1. 题目

2.7.2. 解题思路

2.7.3. 代码实现

2.8. Leetcode 109. 有序链表转换二叉搜索树

2.8.1. 题目

2.8.2. 解题思路

2.8.2.1. 方法一：分治

2.8.2.2. 方法二：分治 + 中序遍历

2.8.3. 代码实现

2.8.4.1. 方法一

2.8.4.2. 方法二

公告

搜索

常用链接

最新随笔

我的标签

积分与排名

合集 (8)

随笔分类 (155)

随笔档案 (139)

阅读排行榜

评论排行榜

推荐排行榜

最新评论