扫描线算法
扫描线
扫描线:假设有一条竖直的直线,从平面的最左端扫描到最右端,在扫描的过程中,直线上的一些线段会被给定的矩形覆盖。如果我们将这些覆盖的线段长度进行积分,就可以得到矩形的面积之和。
如图所示,我们可以把整个矩形分成如图各个颜色不同的小矩形,那么这个小矩形的高就是我们扫过的距离,那么剩下了一个变量,那就是矩形的长一直在变化。
我们的线段树就是为了维护矩形的长,我们给每一个矩形的上下边进行标记:
-
下面的边标记为 \(1\);
-
上面的边标记为 \(-1\)。
每遇到一个矩形时,我们知道了标记为 \(1\) 的边,我们就加进来这一条矩形的长,等到扫描到 \(-1\) 时,证明这一条边需要删除,那么我们就删除这条边,利用 \(1\) 和 \(-1\) 可以轻松得到这种状态。
还要注意这里的线段树指的并不是线段的一个端点,而指的是一个区间,所以我们要计算的是 \(r+1\) 和 \(r-1\)。
注意,需要 离散化。
应用
应用1:Leetcode 253. 会议室 II
题目
给你一个会议时间安排的数组 intervals ,每个会议时间都会包括开始和结束的时间 intervals[i] = [starti, endi] ,返回 所需会议室的最小数量 。
示例 1:
输入:intervals = [[0,30],[5,10],[15,20]]
输出:2
解题思路
标准扫描线算法,把每个会议的起始时间标记为 \(+1\),结束时间标记为 \(-1\),然后将每个时间节点排序,排序时,如果时间相同 \(flag = 1\) 的节点排在 \(flag = -1\) 的节点前面。
然后,依次遍历所有的节点,统计每个节点的最大会议室数目即可。
代码实现
from typing import List
class Node(object):
def __init__(self, _time: int, flag: int):
self.time = _time
self.flag = flag
def __lt__(self, other):
if self.time == other.time:
return self.flag < other.flag
else:
return self.time < other.time
class Solution:
def minMeetingRooms(self, intervals: List[List[int]]) -> int:
if not intervals:
return 0
nodes = list()
for interval in intervals:
nodes.append(Node(interval[0], 1))
nodes.append(Node(interval[1], -1))
nodes.sort()
count = 0
max_count = 0
for node in nodes:
if node.flag == 1:
count += 1
else:
count -= 1
max_count = max(max_count, count)
return max_count
类似的题目
应用2:Lintcode 821. Time Intersection
题目
- Time Intersection
Give two users' ordered online time series, and each section records the user's login time point x and offline time point y. Find out the time periods when both users are online at the same time, and output in ascending order.
Example 1:
Input: seqA = [(1,2),(5,100)], seqB = [(1,6)]
Output: [(1,2),(5,6)]
Explanation: In these two time periods (1,2), (5,6), both users are online at the same time.
Example 2:
Input: seqA = [(1,2),(10,15)], seqB = [(3,5),(7,9)]
Output: []
Explanation: There is no time period, both users are online at the same time.
解题思路
扫描线算法,把起点和终点分别记录为\(1\) 和 \(0\),表示上线 和下线,然后按照 \(time\) 排序。
注意,需要从 \(count = 2\) 时,开始记录起始时刻,\(count\) 从 \(2\) 下降时,则记录结束时刻;
下降的时候,一定要从 \(count = 2\) 的时候开始记录,否则, $1 \to 0 $ 也会被记录进去。
时间复杂度: \((n+m) \times \log_2(n+m)\)
代码实现
/**
* Definition of Interval:
* public classs Interval {
* int start, end;
* Interval(int start, int end) {
* this.start = start;
* this.end = end;
* }
* }
*/
public class Solution {
/**
* @param seqA: the list of intervals
* @param seqB: the list of intervals
* @return: the time periods
*/
private class Node {
public int time;
public int flag;
public Node(int time, int flag) {
this.time = time;
this.flag = flag;
}
}
public List<Interval> timeIntersection(List<Interval> seqA, List<Interval> seqB) {
List<Node> list = new ArrayList<>();
List<Interval> result = new ArrayList<>();
for(Interval interA: seqA) {
list.add(new Node(interA.start, 1));
list.add(new Node(interA.end, -1));
}
for(Interval interB: seqB) {
list.add(new Node(interB.start, 1));
list.add(new Node(interB.end, -1));
}
Collections.sort(list, (a, b) -> (a.time != b.time ? a.time - b.time : a.flag - b.flag));
int count = 0;
int start = -1; int end = -1;
for(Node node: list) {
if(node.flag == 1) {
count++;
if(count == 2) {
start = node.time;
}
}
if(node.flag == -1) {
if(count == 2) {
end = node.time;
result.add(new Interval(start, end));
start = -1;
end = -1;
}
count--;
}
}
return result;
}
}
应用3:Leetcode 218. 天际线问题
题目
解题思路
将所有的建筑物边界排序,排序规则如下:
-
x坐标小的在前面;
-
x坐标相同时,高度较大的在前面;
我们维护一个大根堆,用于在扫描线移动过程中,获取每个位置的最大高度。
代码实现
import heapq
from typing import List
class Solution:
def getSkyline(self, buildings: List[List[int]]) -> List[List[int]]:
result = list()
if not buildings:
return result
boundaries = list()
for building in buildings:
boundaries.append((building[0], building[2]))
boundaries.append((building[1], -building[2]))
# 排序规则:x坐标小的在前面,x坐标相同时,高度较大的在前面
boundaries.sort(key=lambda x: (x[0], -x[1]))
pre_height = 0
# 这里我们需要维护一个大根堆,使较大的高度在堆顶
pq = list()
heapq.heappush(pq, 0)
for boundary in boundaries:
# 如果遇到左侧的边界,就将其加入优先级队列
if boundary[1] > 0:
# 大根堆,所以要取高度的负值
heapq.heappush(pq, -boundary[1])
# 如果遇到右侧的边界,就将右侧的边界出队
else:
# 移除该右侧边界
pq.remove(boundary[1])
heapq.heapify(pq)
# 获取堆顶的元素的高度,注意取负值
current = -pq[0]
if current != pre_height:
result.append([boundary[0], current])
pre_height = current
return result
应用4:Leetcode 759. 员工空闲时间
题目
给定员工的 schedule 列表,表示每个员工的工作时间。每个员工都有一个非重叠的时间段 Intervals 列表,这些时间段已经排好序。
返回表示 所有 员工的 共同,正数长度的空闲时间 的有限时间段的列表,同样需要排好序。
示例 1:
输入:schedule = [[[1,2],[5,6]],[[1,3]],[[4,10]]]
输出:[[3,4]]
解释:
共有 3 个员工,并且所有共同的
空间时间段是 [-inf, 1], [3, 4], [10, inf]。
我们去除所有包含 inf 的时间段,因为它们不是有限的时间段。
解题思路
算法步骤:
-
先将所有的员工的时间段,离散化,将开始时刻标记为 1,结束时刻标记为 -1,并保存在列表 \(event\) 中;
-
对所有时刻,按照起始时间升序排序,如果时刻相同,则按照标志位降序排序,即如果开始和结束时刻相同,则开始时刻在前面;
-
遍历所有的时刻,并记录当前的状态,遇到一个起始时刻,状态变量 \(balance\) 加 1;遇到一个结束时刻,就减 1。
-
当 \(balance\) 为零时,说明该时间段为空闲时段,并将上一个结束时刻作为空闲时段的开始时刻,当前时刻作为空闲时段的结束时刻。
代码实现
class Solution:
def employeeFreeTime(self, schedule: '[[Interval]]') -> '[Interval]':
events = list()
for employee in schedule:
for interval in employee:
events.append((interval.start, 1))
events.append((interval.end, -1))
events.sort(key = lambda x : (x[0], -x[1]))
results = list()
last = None
balance = 0
for _time, state in events:
if balance == 0 and last:
results.append(Interval(last, _time))
if state == 1:
balance += 1
else:
balance -= 1
last = _time
return results
应用5:Leetcode 986. 区间列表的交集
题目
给定两个由一些 闭区间 组成的列表,firstList 和 secondList ,其中 firstList[i] = [starti, endi] 而 secondList[j] = [startj, endj] 。每个区间列表都是成对 不相交 的,并且 已经排序 。
返回这 两个区间列表的交集 。
形式上,闭区间 [a, b](其中 a <= b)表示实数 x 的集合,而 a <= x <= b 。两个闭区间的 交集 是一组实数,要么为空集,要么为闭区间。例如,[1, 3] 和 [2, 4] 的交集为 [2, 3] 。
示例 1:
输入:firstList = [[0,2],[5,10],[13,23],[24,25]], secondList = [[1,5],[8,12],[15,24],[25,26]]
输出:[[1,2],[5,5],[8,10],[15,23],[24,24],[25,25]]
解题思路
算法步骤:
-
先将两个列表的时间段,离散化,将开始时刻标记为 1,结束时刻标记为 -1,并保存在列表 \(event\) 中;
-
对所有时刻,按照起始时间升序排序,如果时刻相同,则按照标志位降序排序,即如果开始和结束时刻相同,则开始时刻在前面;
-
遍历所有的时刻,并记录当前的状态,遇到一个起始时刻,状态变量 \(balance\) 加 1;遇到一个结束时刻,就减 1。
-
当 $balance = 1 $ 并且上一个时刻 \(balance = 2\) 时,说明上一个时间段为重合时段,并将上一个开始时刻作为重叠时段的开始时刻,当前时刻作为重叠时段的结束时刻。
代码实现
class Solution:
def intervalIntersection(self, firstList: List[List[int]], secondList: List[List[int]]) -> List[List[int]]:
events = list()
for interval in firstList:
events.append((interval[0], 1))
events.append((interval[1], -1))
for interval in secondList:
events.append((interval[0], 1))
events.append((interval[1], -1))
events.sort(key=lambda x: (x[0], -x[1]))
result = list()
balance = 0
last_balance = 0
last_time = None
for event in events:
if event[1] == 1:
balance += 1
else:
balance -= 1
if last_balance == 2 and balance == 1:
result.append([last_time, event[0]])
last_balance = balance
last_time = event[0]
return result
应用6:Leetcode 56. 合并区间
题目
解题思路
方法一:扫描线
算法步骤:
-
先将所有的时间段,离散化,将开始时刻标记为 1,结束时刻标记为 -1,并保存在列表 \(event\) 中;
-
对所有时刻,按照起始时间升序排序,如果时刻相同,则按照标志位降序排序,即如果开始和结束时刻相同,则开始时刻在前面;
-
遍历所有的时刻,并记录当前的状态,遇到一个起始时刻,状态变量 \(balance\) 加 1;遇到一个结束时刻,就减 1。
-
对于每一个 \(event\):
-
当 \(balance\) 从 0 增加到 1 时,记录此时为一个待合并区间的起始时刻,记为 \(t_1\);
-
当 \(balance\) 从 1 减少到 0 时,记录此时为一个待合并区间的结束时刻,记为 \(t_2\);
因此,合并后的区间就是:\([t_1, t_2]\)。
-
方法二:排序
算法步骤:
-
首先,我们将列表中的区间按照左端点升序排序。
-
然后我们将第一个区间加入 \(result\) 数组中,并按顺序依次考虑之后的每个区间:
-
如果当前区间的左端点,在数组 \(result\) 中最后一个区间的右端点之后,则它们不会重合;
我们可以直接将这个区间加入数组 \(result\) 的末尾;
-
如果当前区间的左端点,在数组 \(result\) 中最后一个区间的右端点之前,则它们一定会有重合部分。
我们需要用当前区间的右端点,更新数组 \(result\) 中最后一个区间的右端点,将其置为二者的较大值。
-
代码实现
class Solution:
def merge(self, intervals: List[List[int]]) -> List[List[int]]:
events = list()
for interval in intervals:
events.append((interval[0], 1))
events.append((interval[1], -1))
events.sort(key = lambda x : (x[0], -x[1]))
results = list()
balance = 0
last_balance = 0
last_time = 0
for event in events:
if event[1] == 1:
balance += 1
if balance == 1:
last_time = event[0]
else:
balance -= 1
if last_balance == 1 and balance == 0:
results.append([last_time, event[0]])
last_balance = balance
return results
【方法二】
class Solution:
def merge(self, intervals: List[List[int]]) -> List[List[int]]:
_intervals = sorted(intervals, key=lambda x: (x[0], -x[1]))
# 将第一个区间作为基准
result = [_intervals[0]]
for interval in _intervals[1:]:
# 区间相交,result[-1][1]表示结果中最后一个区间的终点
if interval[0] <= result[-1][1]:
result[-1][1] = max(interval[1], result[-1][1])
# 区间不相交,直接保存当前区间
else:
result.append(interval)
return result
应用7:Leetcode 850. 矩形面积 II
题目
给你一个轴对齐的二维数组 rectangles 。 对于 rectangle[i] = [x1, y1, x2, y2],其中(x1,y1)是矩形 i 左下角的坐标, (xi1, yi1) 是该矩形 左下角 的坐标, (xi2, yi2) 是该矩形 右上角 的坐标。
计算平面中所有 rectangles 所覆盖的 总面积 。任何被两个或多个矩形覆盖的区域应只计算 一次 。返回 总面积 。因为答案可能太大,返回 \(10^9 + 7\) 的 模 。
示例 1:
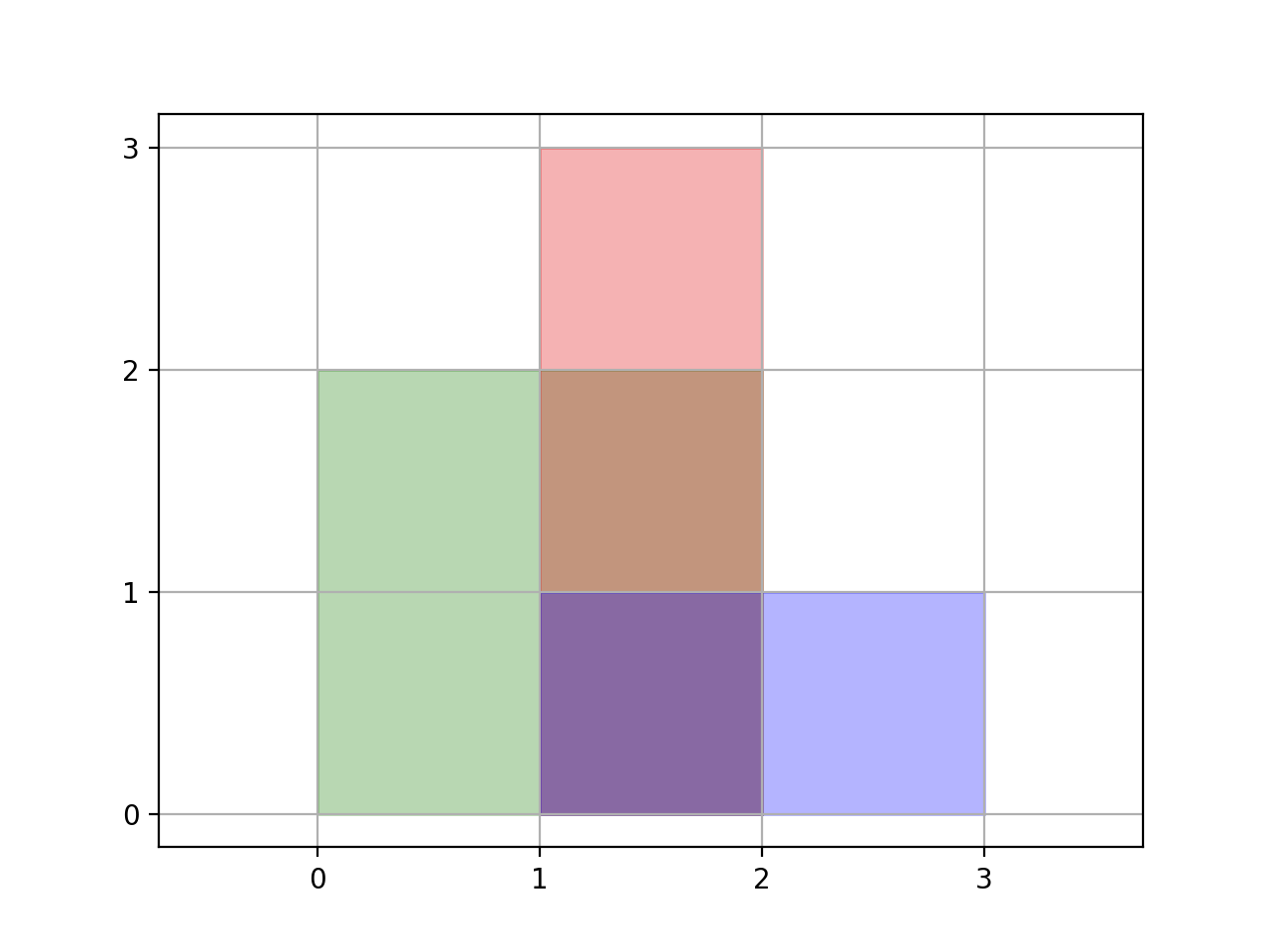
输入:rectangles = [[0,0,2,2],[1,0,2,3],[1,0,3,1]]
输出:6
解释:如图所示,三个矩形覆盖了总面积为 6 的区域。
从(1,1)到(2,2),绿色矩形和红色矩形重叠。
从(1,0)到(2,3),三个矩形都重叠。
解题思路
方法一:扫描线
如下图所示,将所有给定的矩形的左右边界对应的 x 端点提取出来并排序,每个端点可看作是一条竖直的线段(红色),问题转换为求解「由多条竖直线段分割开」的多个矩形的面积总和(黄色):
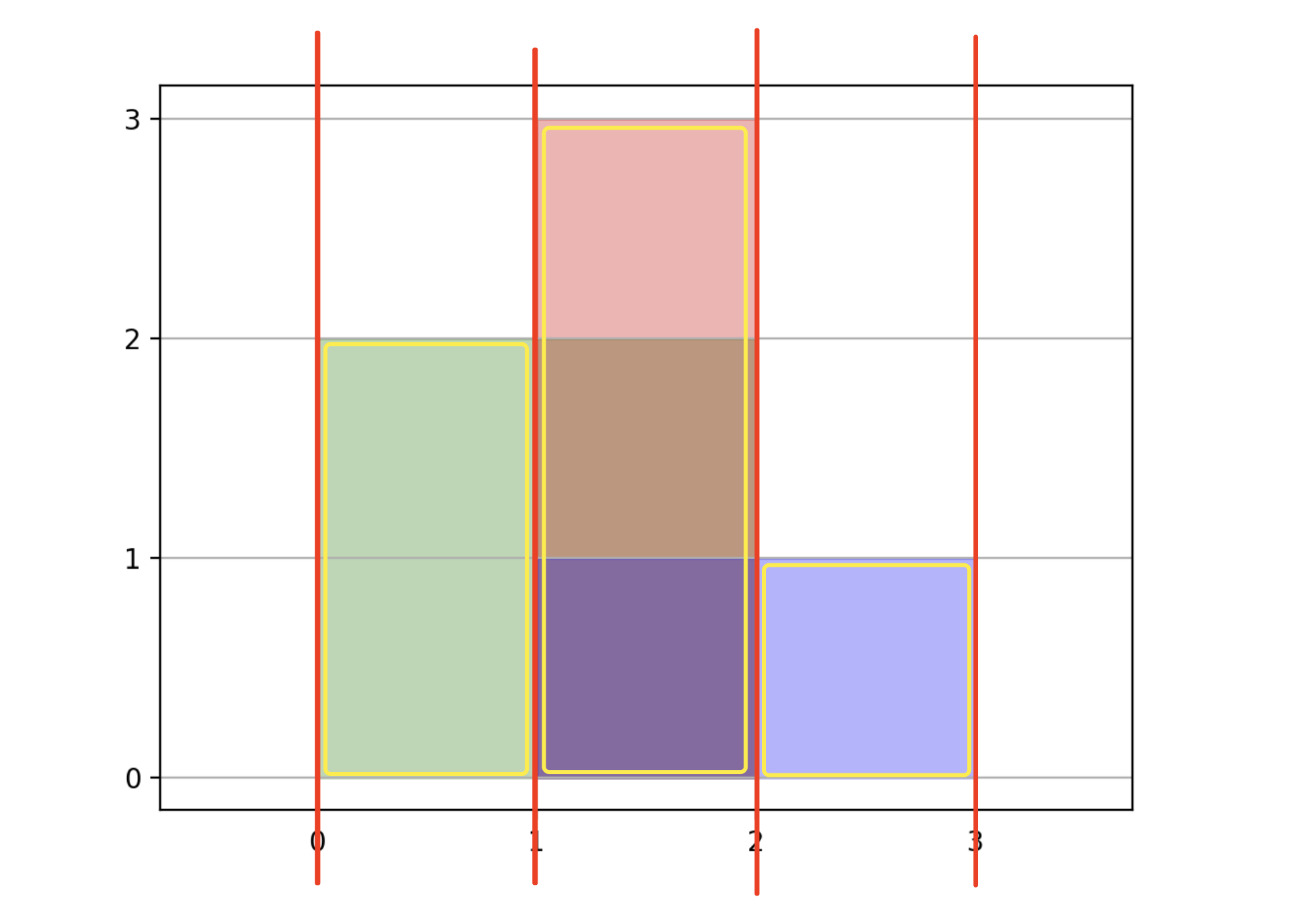
每个相邻线段之间的宽度为单个矩形的「宽度」,可以通过 x 差值直接算得,那么,问题转换为求多个区间内高度的并集,即子矩形的高度,可以使用合并区间的方法求解。
每个区间内的线段总长度就是子矩形的高度,从而就可以得到子矩形的面积了。最后,将所有的区间内的矩形面积相加,即可得到总的覆盖范围了。
方法二:离散化 + 扫描线
思路
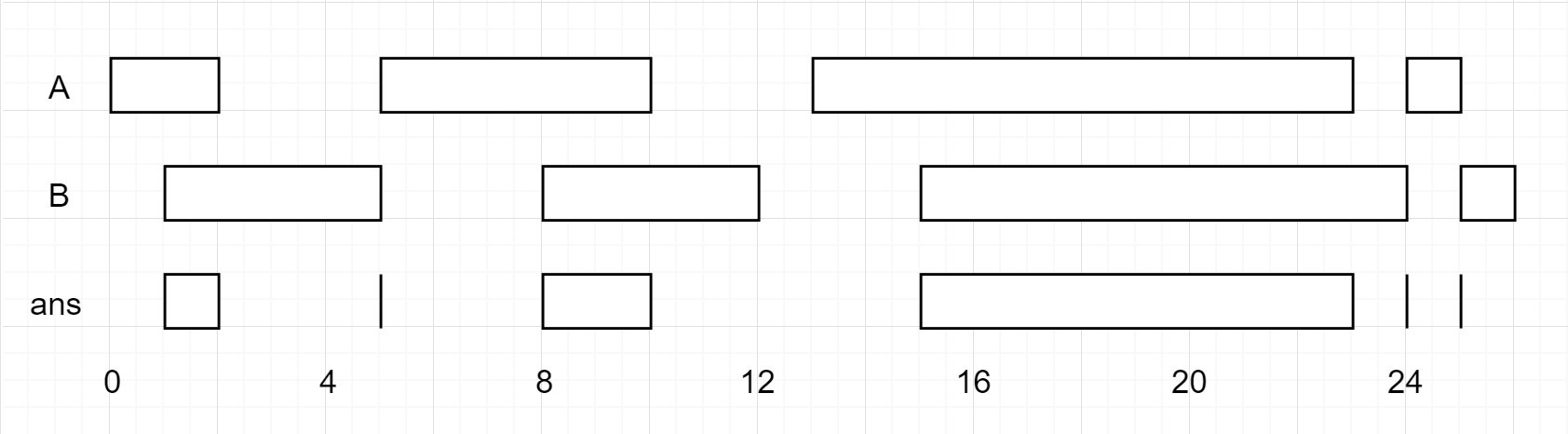
如下图所示,每个矩形都有一个左边界和一个右边界,我们假设有一条竖直的直线从左向右扫描:

假设矩形 \(rectangles\) 的个数为 \(n\) ,那么,矩形的横坐标个数为 \(2n\),因此,扫描线在水平移动过程中,被覆盖的线段长度最多变化 \(2n\) 次,此时,我们就可以将两次变化之间的部分合并起来,一起计算:即这一部分矩形的面积,等于所有被覆盖的线段长度,乘以扫描线在水平方向移动过的距离。
这里会有一个问题,我们如何维护「覆盖的线段长度」呢?
这里同样可以使用到离散化的技巧,扫描线就是一种离散化的技巧,将大范围的连续的坐标转化成 \(2n\) 个离散的坐标。由于矩形的上下边界也是 \(2n\) 个,它们会将 \(y\) 轴分成 \(2n+1\) 个部分,中间的 \(2n−1\) 个部分均为线段,可能会被矩形覆盖。
最外侧的 \(2\) 个部分为射线,不会被矩形覆盖到,并且每一个线段要么完全被覆盖,要么完全不被覆盖。
对于扫描线上的所有线段,我们可以使用一个列表,维护其被覆盖的次数即:
-
当扫描线遇到一个左边界时,我们就将左边界覆盖到的所有线段对应的覆盖次数加 \(1\);
-
当扫描线遇到一个右边界时,我们就将右边界覆盖到的所有线段对应的覆盖次数减 \(1\)。
我们可以从左向右扫描,对于每次处理一部分相同的横坐标,再找到这些横坐标对应的矩形的纵坐标,并记录这条线段的覆盖状态。然后,我们累加扫描线上所有被覆盖的线段长度,就可以得到被覆盖矩形的纵向的高度。
最后,对于这部分相同的横坐标,它们被覆盖的面积为水平宽度乘以纵向的高度。用同样的方式,处理每一个横坐标,并累加面积即可得到答案。
算法步骤
-
我们使用列表 \(verticalBoundaries\) 保存所有矩形的上下边界,再对其去重,并按照从小到大的顺序排序。
注意,由于我们对矩形的上下边界排序了,所以,我们需要引入一个列表 \(coverTimes\) 来记录所有上下边界组成的线段的覆盖状态。
-
同时,使用列表 \(horizonBoundaries\) 记录所有矩形的矩形的左右边界信息:\((x, i, coverFlag)\),其中,\(x\) 为该矩形边界的横坐标,\(i\) 为该矩形的索引,\(coverFlag\) 为覆盖标记:左边界标记为 \(1\),右边界标记为 \(-1\)。
然后,我们对所有 \(horizonBoundaries\) 记录的左右边界信息,并按照横坐标从小到大的顺序排序。
-
遍历所有矩形的左右边界 \(horizonBoundaries[i]\) ,并跳过所有横坐标相同的左右边界,并找到第一个不相同的横坐标的序号 \(j\)。
那么,当前扫描的区间宽度 \(width\) 就是两个横坐标之差。
-
依次遍历这些相同的横坐标,对于每一个横坐标:
-
通过索引找到它们对应的矩形的纵坐标:\(y_1\),\(y_2\),那么,它们能覆盖的纵向范围就是:\([y_1,y_2]\)。
-
遍历 \(verticalBoundaries\) 中的所有纵向线段,如果该线段在 \([y_1,y_2]\) 覆盖范围内,就更新该线段的标记值。
-
-
遍历所有的纵向线段,累加被覆盖的线段,将其作为当前覆盖区域的高度 \(height\)。
-
计算当前覆盖区域的面积:\(S_i = height \times width\)。
注意,累加的面积时候,每次累加完之后,可以进行一次模运算,这样可以加快计算速度。
-
继续遍历其他的横坐标,并重复上述步骤。
方法三:线段树
方法二中对于数组 \(coverTimes\) 的所有操作,都可以使用线段树进行维护。线段树中需要存储:
-
该节点对应的区间被完整覆盖的次数;
-
该节点对应的区间被覆盖的线段长度。
线段树需要支持:
-
区间增加 1;
-
区间减少 1,并且保证每个被增加 1 的区间在之后一定会减少 1;
-
对于所有非 0 的位置,根据它们的权值进行求和。
由于这种方法严重超纲,因此不在这里详细阐述。
代码实现
【方法一】
from typing import List, Tuple
MOD = 1000000007
class Solution:
def rectangleArea(self, rectangles: List[List[int]]) -> int:
# 记录左右边界 [x1, x2]
boundaries = []
for rectangle in rectangles:
boundaries.append(rectangle[0])
boundaries.append(rectangle[2])
boundaries.sort()
result = 0
for i in range(1, len(boundaries)):
x1, x2 = boundaries[i - 1], boundaries[i]
# 子矩形的水平宽度
width = x2 - x1
if width == 0:
continue
# 找到所有覆盖当前子区间的矩形,并记录其上下边界
lines = list()
for rectangle in rectangles:
if rectangle[0] <= x1 and x2 <= rectangle[2]:
lines.append((rectangle[1], rectangle[3]))
height = self.count_length(lines)
result += height * width
return result % MOD
@classmethod
def count_length(cls, intervals: List[Tuple[int, int]]):
""" 计算所有子区间的长度,区间可能重叠
:param intervals:
:return:
"""
intervals.sort()
length, start, end = 0, -1, -1
for interval in intervals:
# 记录新的区间
if interval[0] > end:
# 累加区间长度
length += end - start
# 记录新的区间范围
start, end = interval
# 合并区间
elif interval[1] > end:
end = interval[1]
length += end - start
return length
【方法二】
from typing import List, Tuple
MOD = 1000000007
class Solution:
def rectangleArea(self, rectangles: List[List[int]]) -> int:
# m 个纵坐标最多可以将平行于Y轴的扫描线分成 m - 1 个区间(去掉两端的射线)
vertical_boundaries = set()
for rectangle in rectangles:
vertical_boundaries.add(rectangle[1])
vertical_boundaries.add(rectangle[3])
vertical_boundaries = sorted(vertical_boundaries)
m = len(vertical_boundaries)
horizon_boundaries = list() # 记录所有的横坐标
for i, rectangle in enumerate(rectangles):
horizon_boundaries.append((rectangle[0], i, 1))
horizon_boundaries.append((rectangle[2], i, -1))
# 将矩形的所有左右边界按从小到大的顺序排序
horizon_boundaries.sort()
# 记录Y轴上每一个线段的状态
cover_times = [0] * (m - 1)
result = 0
i = 0
# 扫描线水平从左向右扫描所有的X坐标
while i < len(horizon_boundaries):
j = i + 1
# 找到第一个不相等的横坐标
while j < len(horizon_boundaries) and horizon_boundaries[i][0] == horizon_boundaries[j][0]:
j += 1
if j == len(horizon_boundaries):
break
# 遍历 [i, j - 1] 范围内的 x 坐标,更新它们对应的纵向线段的覆盖状态
for k in range(i, j):
_, index, diff = horizon_boundaries[k]
# 找到这些 x 坐标所对应的上下边界的纵坐标 y1, y2
y1, y2 = rectangles[index][1], rectangles[index][3]
# 遍历所有的纵向线段,线段有两种状态:线段被矩形覆盖;不在矩形覆盖范围内。
for p in range(m - 1):
# 如果该线段在 [y1, y2] 覆盖范围内,就更新其状态
if y1 <= vertical_boundaries[p] and vertical_boundaries[p + 1] <= y2:
cover_times[p] += diff
# 求扫描线上被矩形覆盖的线段之和,也就是高度
height = 0
# 遍历所有的纵向线段
for p in range(m - 1):
# 如果线段它被矩形覆盖,其高度一定是两个相邻线段的差值
if cover_times[p] > 0:
height += (vertical_boundaries[p + 1] - vertical_boundaries[p])
# 计算扫描线经过范围内被覆盖的面积
result += height * (horizon_boundaries[j][0] - horizon_boundaries[i][0])
result %= MOD
i = j
return result
【方法三】
import bisect
from typing import List
class Segtree:
def __init__(self):
self.cover = 0
self.length = 0
self.max_length = 0
@classmethod
def init(cls, tree: List["Segtree"], idx: int, l: int, r: int, hbound: List[int]) -> None:
tree[idx].cover = tree[idx].length = 0
if l == r:
tree[idx].max_length = hbound[l] - hbound[l - 1]
return
mid = (l + r) // 2
cls.init(tree, idx * 2, l, mid, hbound)
cls.init(tree, idx * 2 + 1, mid + 1, r, hbound)
tree[idx].max_length = tree[idx * 2].max_length + tree[idx * 2 + 1].max_length
@classmethod
def update(cls, tree: List["Segtree"], index: int, l: int, r: int, ul: int, ur: int, diff: int) -> None:
if l > ur or r < ul:
return
if ul <= l and r <= ur:
tree[index].cover += diff
cls.pushup(tree, index, l, r)
return
mid = (l + r) // 2
cls.update(tree, index * 2, l, mid, ul, ur, diff)
cls.update(tree, index * 2 + 1, mid + 1, r, ul, ur, diff)
cls.pushup(tree, index, l, r)
@classmethod
def pushup(cls, tree: List["Segtree"], idx: int, l: int, r: int) -> None:
if tree[idx].cover > 0:
tree[idx].length = tree[idx].max_length
elif l == r:
tree[idx].length = 0
else:
tree[idx].length = tree[idx * 2].length + tree[idx * 2 + 1].length
class Solution:
def rectangleArea(self, rectangles: List[List[int]]) -> int:
hbound = set()
for rectangle in rectangles:
# 下边界
hbound.add(rectangle[1])
# 上边界
hbound.add(rectangle[3])
hbound = sorted(hbound)
m = len(hbound)
# 线段树有 m-1 个叶子节点,对应着 m-1 个会被完整覆盖的线段,需要开辟 ~4m 大小的空间
tree = [Segtree() for _ in range(m * 4 + 1)]
Segtree.init(tree, 1, 1, m - 1, hbound)
sweep = list()
for i, rectangle in enumerate(rectangles):
# 左边界
sweep.append((rectangle[0], i, 1))
# 右边界
sweep.append((rectangle[2], i, -1))
sweep.sort()
result = 0
i = 0
while i < len(sweep):
j = i
while j + 1 < len(sweep) and sweep[i][0] == sweep[j + 1][0]:
j += 1
if j + 1 == len(sweep):
break
# 一次性地处理掉一批横坐标相同的左右边界
for k in range(i, j + 1):
_, index, diff = sweep[k]
# 使用二分查找得到完整覆盖的线段的编号范围
left = bisect.bisect_left(hbound, rectangles[index][1]) + 1
right = bisect.bisect_left(hbound, rectangles[index][3])
Segtree.update(tree, 1, 1, m - 1, left, right, diff)
result += tree[1].length * (sweep[j + 1][0] - sweep[j][0])
i = j + 1
return result % (10 ** 9 + 7)
参考:



 浙公网安备 33010602011771号
浙公网安备 33010602011771号