子序列问题
应用
| 序号 | 题目 | 备注 |
|---|---|---|
| 1 | 300. 最长递增子序列 | |
| 2 | 674. 最长连续递增序列 | |
| 3 | 718. 最长重复子数组 | |
| 4 | 1143. 最长公共子序列 | 参考:最长公共子序列 |
| 5 | 1035. 不相交的线 | |
| 6 | 53. 最大子序和 | |
| 7 | 392. 判断子序列 | |
| 8 | 115. 不同的子序列 | |
| 9 | 583. 两个字符串的删除操作 | 参考:最长公共子序列 |
| 10 | 72. 编辑距离 | 参考:编辑距离 |
| 11 | 647. 回文子串 | |
| 12 | 516. 最长回文子序列 |
应用1:Leetcode 300. 最长递增子序列
题目
给你一个整数数组 nums ,找到其中最长严格递增子序列的长度。
子序列 是由数组派生而来的序列,删除(或不删除)数组中的元素而不改变其余元素的顺序。例如,[3,6,2,7] 是数组 [0,3,1,6,2,2,7] 的子序列。
示例 1:
输入:nums = [10,9,2,5,3,7,101,18]
输出:4
解释:最长递增子序列是 [2,3,7,101],因此长度为 4 。
分析
设 \(dp[i]\) 表示以 \(nums[i]\) 结尾的最长递增子序列的长度。
由于,对于以 \(nums[0]\) 结尾,并且,长度为 \(1\) 的子序列,它是一个升序序列,因此:
因此,对于任意一个以 \(num[i]\) 结尾的子序列,我们只需要在 \([0, i - 1]\) 范围内,找到最长的一个递增子序列,进行转移即可。
即我们需要在 \([0, i - 1]\) 范围内,找到一个最大的 \(dp[j]\) 进行状态转移,因此,状态转移方程为:
其中,\(dp[j]\) 表示在 \(nums[0 \cdots i - 1]\) 中,满足条件 \(nums[j] < nums[i]\),并且,它是最大的一个。
代码实现
class Solution:
def lengthOfLIS(self, nums: List[int]) -> int:
dp = [1 for _ in range(len(nums))]
for i in range(len(nums)):
for j in range(0, i):
if nums[i] > nums[j]:
dp[i] = max(dp[i], dp[j] + 1)
result = 0
for i in range(len(dp)):
result = max(result, dp[i])
return result
扩展
这里也可以使用二分插入的思路,进行查找插入位置。
应用2:Leetcode 674. 最长连续递增序列
题目
给定一个未经排序的整数数组,找到最长且 连续递增的子序列,并返回该序列的长度。
连续递增的子序列 可以由两个下标 l 和 r(l < r)确定,如果对于每个 l <= i < r,都有 nums[i] < nums[i + 1] ,那么子序列 [nums[l], nums[l + 1], ..., nums[r - 1], nums[r]] 就是连续递增子序列。
示例 1:
输入:nums = [1,3,5,4,7]
输出:3
解释:最长连续递增序列是 [1,3,5], 长度为3。
尽管 [1,3,5,7] 也是升序的子序列, 但它不是连续的,因为 5 和 7 在原数组里被 4 隔开。
分析
方法一:贪心算法
为了得到最长连续递增序列,可以使用贪心的策略得到尽可能长的连续递增序列。
具体的做法是:
-
从左到右遍历数组;
-
将子序列的起始下标 start 设置为 0;
-
遍历数组的过程中每次比较相邻元素,
-
如果相邻元素递减,则更新起始下标 start 为当前位置;
-
否则,就起始下标就保持不变。
-
-
每遍历一个元素,就记录当前连续递增子序列的长度,同时更新最长的递增子序列长度。
方法二:双指针
维护两个指针 \(i\)、\(j\) 用于记录最长递增子序列的区间,不断移动右指针,遇到递减序列,就将左指针移动到右指针的位置,同时,记录子序列的区间长度。
代码实现
方法一
class Solution:
def findLengthOfLCIS(self, nums: List[int]) -> int:
result = 0
n = len(nums)
start = 0
for i in range(n):
if i > 0 and nums[i] <= nums[i - 1]:
start = i
result = max(result, i - start + 1)
return result
方法二
class Solution:
def findLengthOfLCIS(self, nums: List[int]) -> int:
n = len(nums)
result = 1
i, j = 0, 0
while i < n and j < n:
while j < n and nums[j - 1] < nums[j]:
j += 1
result = max(result, j - i)
i = j
j += 1
return result
应用3:Leetcode 300. 最长递增子序列
题目
给两个整数数组 nums1 和 nums2 ,返回 两个数组中 公共的 、长度最长的子数组的长度 。
示例 1:
输入:nums1 = [1,2,3,2,1], nums2 = [3,2,1,4,7]
输出:3
解释:长度最长的公共子数组是 [3,2,1] 。
分析
设 \(dp[i][j]\) 表示以 \(nums1[i - 1]\) 结尾的子数组与以 \(nums2[j - 1]\) 结尾的子数组的最长公共后缀的长度。
当两个子数组,有任意一个数组长度为 \(0\) 时,两者的公共子序列长度都为 \(0\),因此,有:
对于任意长度的两个子数组,我们可以遍历两个子数组,对于当前元素 \(nums1[i - 1]\) 和 \(nums2[j - 1]\):
-
如果 \(nums2[j - 1] = nums2[j - 1]\),则说明他们可以通过,以 \(nums1[i - 2]\) 和 \(nums2[j - 2]\) 结尾的子数组转移而来,即通过状态 \(dp[i - 1][j - 1]\) 转移过来;
-
如果 \(nums2[j - 1] \ne nums2[j - 1]\),则以 \(nums1[i - 1]\) 和 \(nums2[j - 1]\) 结尾的两个子数组公共长度为 \(0\)。
因此,状态转移方程
代码实现
class Solution:
def findLength(self, nums1: List[int], nums2: List[int]) -> int:
m, n = len(nums1), len(nums2)
dp = [[0 for _ in range(n + 1)] for _ in range(m + 1)]
result = 0
for i in range(1, m + 1):
for j in range(1, n + 1):
if nums1[i - 1] == nums2[j - 1]:
dp[i][j] = dp[i - 1][j - 1] + 1
else:
dp[i][j] = 0
result = max(result, dp[i][j])
return result
应用4:1143. 最长公共子序列
参考:
应用5:1035. 不相交的线
题目
在两条独立的水平线上按给定的顺序写下 nums1 和 nums2 中的整数。
现在,可以绘制一些连接两个数字 nums1[i] 和 nums2[j] 的直线,这些直线需要同时满足满足:
nums1[i] == nums2[j]
且绘制的直线不与任何其他连线(非水平线)相交。
请注意,连线即使在端点也不能相交:每个数字只能属于一条连线。以这种方法绘制线条,并返回可以绘制的最大连线数。
示例 1:
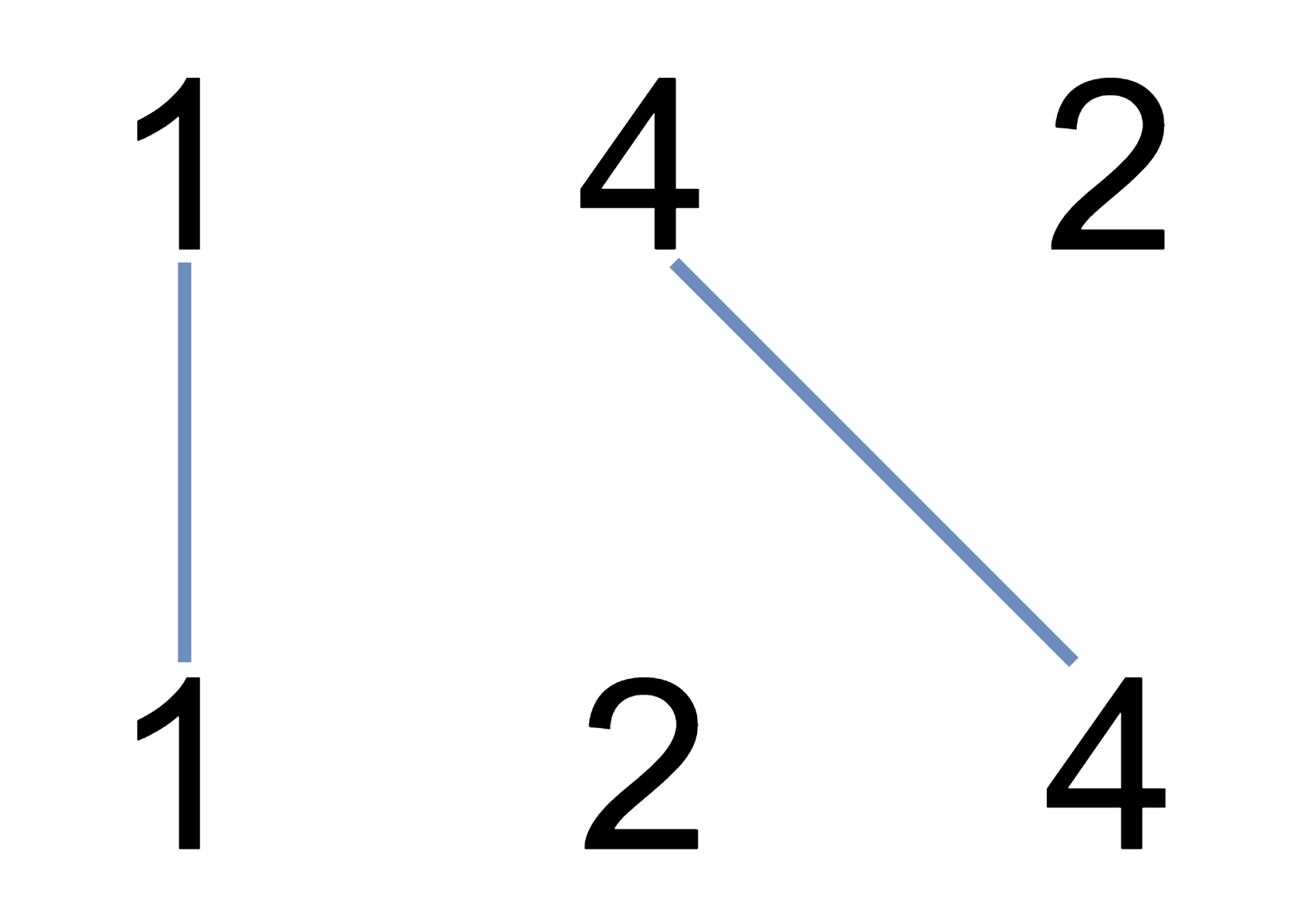
输入:nums1 = [1,4,2], nums2 = [1,2,4]
输出:2
解释:可以画出两条不交叉的线,如上图所示。 但无法画出第三条不相交的直线,因为从 nums1[1]=4 到 nums2[2]=4 的直线将与从 nums1[2]=2 到 nums2[1]=2 的直线相交。
分析
这里,需要注意,题目中的两个子序列连接后不相交,必然满足子序列是两个数组的最长公共子序列,因此,题目就可以转换为求解两个数组的最长公共子序列。
动态规划
设 \(dp[i][j]\) 表示以 \(nums1[i - 1]\) 结尾的子数组与以 \(nums2[j - 1]\) 结尾的子数组的最长公共后缀的长度。
边界条件
当两个子数组,有任意一个数组长度为 \(0\) 时,两者的公共子序列长度都为 \(0\),因此,有:
状态转移
对于任意长度的两个子数组,我们可以遍历两个子数组,对于当前元素 \(nums1[i - 1]\) 和 \(nums2[j - 1]\):
-
如果 \(nums2[j - 1] = nums2[j - 1]\),则说明他们可以通过,以 \(nums1[i - 2]\) 和 \(nums2[j - 2]\) 结尾的子数组转移而来,即通过状态 \(dp[i - 1][j - 1]\) 转移过来;
-
如果 \(nums2[j - 1] \ne nums2[j - 1]\),则以 \(nums1[i - 1]\) 和 \(nums2[j - 1]\) 结尾的两个子数组公共长度为 \(0\)。
因此,状态转移方程
注意,由于 \(dp[i - 1][j - 1] \le dp[i][j - 1]\) 且 \(dp[i - 1][j - 1] \le dp[i - 1][j]\),因此,状态转移方程可以等价于:
代码实现
class Solution:
def maxUncrossedLines(self, nums1: List[int], nums2: List[int]) -> int:
m, n = len(nums1), len(nums2)
dp = [[0 for _ in range(n + 1)] for _ in range(m + 1)]
for i in range(1, m + 1):
for j in range(1, n + 1):
if nums1[i - 1] == nums2[j - 1]:
dp[i][j] = max(dp[i][j], dp[i - 1][j - 1] + 1)
else:
dp[i][j] = max(dp[i][j - 1], dp[i - 1][j])
return dp[m][n]
应用6:Leetcode 53. 最大子序和
题目
给你一个整数数组 nums ,请你找出一个具有最大和的连续子数组(子数组最少包含一个元素),返回其最大和。子数组 是数组中的一个连续部分。
示例 1:
输入:nums = [-2,1,-3,4,-1,2,1,-5,4]
输出:6
解释:连续子数组 [4,-1,2,1] 的和最大,为 6 。
分析
方法一:动态规划
假设 \(dp[i]\) 表示以元素 \(nums[i - 1]\) 结尾的最大连续数组的和,那么,我们要求的和就是每个位置的 \(dp[i]\),然后,返回其中的最大值即可,即:
初始条件
当数组的长度为1时,显然有:
状态转移
遍历数组 \(nums\),对于任意一个元素 \(nums[i]\) ,都有两种选择:
-
当 \(nums[i] < dp[i - 1] + nums[i - 1]\) 时,将元素 \(nums[i]\) 添加到以 \(nums[i - 1]\) 结尾的子数组的末尾;
-
当 \(nums[i] \ge dp[i - 1] + nums[i - 1]\) 时,将元素 \(nums[i]\) 单独作为一个子数组。
因此,状态转移方程为:
方法二:分治
参考:最大子序和
代码实现
方法一
class Solution:
def maxSubArray(self, nums: List[int]) -> int:
n = len(nums)
result = nums[0]
dp = [0 for _ in range(n)]
dp[0] = nums[0]
for i in range(1, n):
if nums[i] + dp[i -1] > nums[i]:
dp[i] = nums[i] + dp[i -1]
else:
dp[i] = nums[i]
result = max(result, dp[i])
return result
【优化后的代码】:
class Solution:
def maxSubArray(self, nums: List[int]) -> int:
n = len(nums)
last = nums[0]
result = nums[0]
for i in range(1, n):
last = max(last + nums[i], nums[i])
result = max(result, last)
return result
应用7:Leetcode 392. 最长递增子序列
题目
给定字符串 s 和 t ,判断 s 是否为 t 的子序列。
字符串的一个子序列是原始字符串删除一些(也可以不删除)字符而不改变剩余字符相对位置形成的新字符串。(例如,"ace"是"abcde"的一个子序列,而"aec"不是)。
示例 1:
输入:s = "abc", t = "ahbgdc"
输出:true
分析
维护两个指针 \(i\)、 \(j\),分别指向字符串 \(s\) 和 \(t\),每次贪心地匹配:
-
如果指针 \(i\)、 \(j\) 指向的字符相等,则同时移动指针 \(i\)、\(j\);
-
如果指针 \(i\)、 \(j\) 指向的字符不相等,则只移动指针 \(j\);
当指针 \(j\) 遍历完字符串 \(t\) 后:
-
若指针 \(i\) 还未到达字符串 \(s\) 的末尾,则 \(s\) 不是 \(t\) 的子序列;
-
若指针 \(i\) 还未到达字符串 \(s\) 的末尾,则 \(s\) 是 \(t\) 的子序列。
代码实现
class Solution:
def isSubsequence(self, s: str, t: str) -> bool:
m, n = len(s), len(t)
i, j = 0, 0
while i < m and j < n:
if s[i] == t[j]:
i += 1
j += 1
return i == m
应用8:Leetcode 115. 不同的子序列
题目
给你两个字符串 s 和 t ,统计并返回在 s 的 子序列 中 t 出现的个数。题目数据保证答案符合 32 位带符号整数范围。
其中,1 <= s.length, t.length <= 1000
示例 1:
输入:s = "rabbbit", t = "rabbit"
输出:3
解释:
如下所示, 有 3 种可以从 s 中得到 "rabbit" 的方案。
ra b bbit
rab b bit
rabb b it
分析
动态规划
假设字符串 \(s\) 和 \(t\) 的长度分别为 \(m\)、\(n\),设 \(dp[i][j]\) 表示在子串 \(s[0 \cdots i - 1]\) 的子序列中,子串 \(t[0 \cdots j - 1]\) 出现的次数。
边界条件
当目标字符串 \(t\) 的长度为 \(0\) 时,即 t 为空串时,它一定是 \(s\) 的子序列。当源字符串 \(s\) 长度为 \(0\) 时,任何非空字符串的都不是它的子序列。
因此,边界条件为:
状态转移
这里,我们以字符串 \(t\) 作为基准字符串,并且,同时遍历源字符串 \(s\) 和基准字符串 \(t\),对于每一对字符 \(s[i - 1]\) 和 \(t[j - 1]\),都有两种情况:
-
如果两者不相等,即 \(s[i - 1] \ne t[j - 1]\)
此时,当前字符 \(s[i - 1]\) 对匹配过程没有参与贡献。
因此,我们只需要考虑子串 \(s[0 \cdots i - 2]\) 中是否包含 \(t[0 \cdots j - 1]\) 即可。
即子串 \(s[0 \cdots i - 1]\) 的子序列中包含子串 \(t[0 \cdots j - 1]\) 的个数,与 \(s[0 \cdots i - 2]\) 的子序列中包含 \(t[0 \cdots j - 1]\) 的个数相同。
因此,当前状态与上一个状态 \(dp[i - 1][j]\) 相同。
-
如果两者相等,即 \(s[i - 1] = t[j - 1]\)
例如,某个时刻,两个子串分别为:\(s[0 \cdots i - 1] = aaabb\),\(t[0 \cdots j - 1] = ab\)。
此时,\(s[4]=t[1]\),而在此之前,\(s[3]\) 已经与 \(t[1]\) 进行匹配了,因此,我们需要同时考虑两种情况:
-
不使用 \(s[4]\) 进行匹配
当前的匹配的次数,就是通过 \(s[0 \cdots i - 2] = aaab\) 中包含 \(t[0 \cdots j - 1] = ab\) 的个数;
-
使用 \(s[4]\) 进行匹配,
当前的匹配的次数,就是通过 \(s[0 \cdots i - 1] = aaabb\) 中包含 \(t[0 \cdots j - 1] = ab\) 的个数。
因此,这种情况下,我们不仅要考虑 \(s\) 中包含当前字符 \(s[i - 1]\) 的子串的贡献,还要考虑去掉当前字符 \(s[i - 1]\) 的子串是否参与贡献。
也就是说,我们需要同时考虑子串 \(s[0 \cdots i - 1]\) 和 \(s[0 \cdots i - 2]\) 中,同时包含的子序列 \(t[j - 1]\) 的个数。
有两种情况:
-
不使用 \(s[i - 1]\) 进行匹配,即字符 \(s[i - 1]\) 没有参与贡献
此时,我们只需要考虑去掉子串 \(s[0 \cdots i - 1]\) 中的 \(s[i - 1]\)即可。
也就是说,当前状态就 \(s[0 \cdots i - 2]\) 的子序列中包含 \(t[0 \cdots j - 1]\) 的个数即可,即匹配的数量与 \(dp[i - 1][j]\) 相同。
-
使用 \(s[i - 1]\) 进行匹配,即字符 \(s[i - 1]\) 参与了贡献
此时,我们只需考虑同时去掉两个子串的最后一个字符 \(s[i - 1]\) 和 \(t[j - 1]\) 即可。
也就是说,当前状态就是 \(s[0 \cdots i - 2]\) 的子序列中包含 \(t[0 \cdots j - 2]\) 的个数,即匹配的数量与 \(dp[i - 1][j - 1]\) 相同。
也就是说,当前状态,可以同时通过上述两种状态转移而来,因此。
-
代码实现
class Solution:
def numDistinct(self, s: str, t: str) -> int:
m, n = len(s), len(t)
dp = [[0 for _ in range(n + 1)] for _ in range(m + 1)]
for i in range(m + 1):
dp[i][0] = 1
for i in range(1, m + 1):
for j in range(1, n + 1):
if s[i - 1] == t[j - 1]:
dp[i][j] = dp[i - 1][j - 1] + dp[i - 1][j]
else:
dp[i][j] = dp[i - 1][j]
return dp[m][n]
应用9:Leetcode 583. 两个字符串的删除操作
参考:最长公共子序列
应用10:Leetcode 72. 编辑距离
参考:编辑距离
应用11:Leetcode 647. 回文子串
题目
给你一个字符串 s ,请你统计并返回这个字符串中 回文子串 的数目。回文字符串 是正着读和倒过来读一样的字符串。
子字符串 是字符串中的由连续字符组成的一个序列。具有不同开始位置或结束位置的子串,即使是由相同的字符组成,也会被视作不同的子串。
示例 1:
输入:s = "abc"
输出:3
解释:三个回文子串: "a", "b", "c"
分析
动态规划
设 \(dp[i][j]\) 表示子串 \(s[i \cdots j]\) 是否是回文子串,若 \(dp[i][j] = True\),则表示子串 \(s[i \cdots j]\) 是回文子串,否则,它就不是回文子串。假设字符串 \(s\) 的长度为 \(n\)。
边界条件
当子串 \(s[i \cdots j]\) 长度为 \(1\) 时,它是一个回文子串,因此边界条件如下:
状态转移
对于字符串 \(s\),我们倒序遍历子串的起始位置 \(i\),同时使用指针 \(j\),从位置 \(i+1\) 开始顺序枚举子串 \(s[i \cdots j]\) 的结束位置。
对于,任意一个子串 \(s[i \cdots j]\) ,存在两种情况,使得它是一个回文串:
-
子串长度为 \(1\),即 \(i = j\);
-
子串长度大于 \(1\),若 \(s[i] = s[j]\),且它的子串 \(s[i + 1 \cdots j - 1]\) 是一个回文串。
这里需要注意,当子串长度为 \(2\) ,即\(j = i + 1\) 时,它的子串 \(s[i + 1 \cdots j - 1]\) 是一个空串
"",需要单独讨论。
否则,它就不是一个回文串。
因此,状态转移方程为:
这里,\(\land\) 表示逻辑与运算,\(\lor\) 表示逻辑或运算。
代码实现
【逆序枚举】
class Solution:
def countSubstrings(self, s: str) -> int:
n = len(s)
dp = [[False] * n for _ in range(n)]
result = 0
for i in range(n - 1, -1, -1):
for j in range(i, n):
if s[i] == s[j] and (j - i <= 1 or dp[i + 1][j - 1]):
result += 1
dp[i][j] = True
return result
【顺序枚举】
顺序遍历的思路也是一样的,都是依次枚举字符串 \(s\) 中的每一个字符,并从小到大枚举每一个子串 \(s[i] \cdots s[j]\)。
这里我们直接给出顺序遍历的示例代码:
class Solution:
def countSubstrings(self, s: str) -> int:
n = len(s)
dp = [[False] * n for _ in range(n)]
result = 0
# 顺序枚举s中的每一个字符
for j in range(n):
# 从小到大,即向左,枚举每一个子串 s[i]...s[j]
for i in range(j, -1, -1):
if s[j] == s[i] and (j - i <= 1 or dp[i + 1][j - 1]):
result += 1
dp[i][j] = True
return result
应用12:Leetcode 516. 最长回文子序列
题目
给你一个字符串 s ,找出其中最长的回文子序列,并返回该序列的长度。
子序列定义为:不改变剩余字符顺序的情况下,删除某些字符或者不删除任何字符形成的一个序列。
示例 1:
输入:s = "bbbab"
输出:4
解释:一个可能的最长回文子序列为 "bbbb" 。
分析
动态规划
假设字符串 \(s\) 的长度为 \(n\),设 \(dp[i][j]\) 表示子串 \(s[i] \cdots s[j]\) 的最长回文子序列的长度,那么,最后要求的答案就是 \(dp[0][n - 1]\)。
显然,当子串中只有一个字符时,它的最长回文子序列的长度为 \(1\),因此,初始条件:
思路:
-
逆序枚举 \(s\) 中的每一个字符 \(s[i]\);
-
同时,顺序枚举子串 \(s[i + 1] \cdots s[n - 1]\) 中的每一个字符 \(s[j]\);
-
对于,字符 \(s[i]\) 和 \(s[j]\),存在有两种情况:
-
\(s[i] = [j]\)
说明当前两个字符,都可以添加到子串 \(s[i + 1] \cdots s[j - 1]\) 的首尾,作为更长的回文子序列,因此,当前状态的最长回文子序列的长度为 \(dp[i + 1][j - 1] + 2\)。
-
\(s[i] \ne [j]\)
说明当前两个字符,同时添加到子串 \(s[i + 1] \cdots s[j - 1]\) 的首尾,不会较上一个状态有变化,因此,当前状态与上一个状态的最大值相同,即要么 \(s[i + 1] \cdots s[j]\) 或者 \(s[i] \cdots s[j - 1]\)。
注:这里我们不需要考虑子串 \(s[i + 1] \cdots s[j - 1]\) 所对应的状态,因为,在子串首部或者尾部添加一个字符,构成的新子串其最长回文序列长度一定不小于原来的长度。
因此,一定会有:\[\begin{aligned} dp[i + 1][j - 1] \le dp[i + 1][j] \\ dp[i + 1][j - 1] \le dp[i][j - 1] \end{aligned} \]
-
因此,状态转移方程为:
代码实现
class Solution:
def longestPalindromeSubseq(self, s: str) -> int:
n = len(s)
dp = [[0 for _ in range(n)] for _ in range(n)]
for i in range(n):
dp[i][i] = 1
for i in range(n - 1, -1, -1):
for j in range(i + 1, n):
if s[i] == s[j]:
dp[i][j] = max(dp[i][j], dp[i + 1][j - 1] + 2)
else:
dp[i][j] = max(dp[i + 1][j], dp[i][j - 1])
return dp[0][n - 1]
参考:


 浙公网安备 33010602011771号
浙公网安备 33010602011771号