欧拉回路

目录

• 欧拉图
  • 定义
  • 性质
  • 判别方法
    • 无向图
    • 有向图
    • 示例
  • 求欧拉回路的方法
    • Fleury 算法
    • Hierholzer 算法
      • 实现
      • 性质
      • 应用
        • 计算机译码
• 应用
  • 应用1：洛谷 P2731 骑马修栅栏
    • 题目
    • 解题思路
    • 代码实现
  • 应用2：Leetcode 753. 破解保险箱
    • 题目
    • 解题思路
      • 题意转换
      • 思路
      • Hierholzer 算法
    • 代码实现
  • 应用3：Leetcode 332. 重新安排行程
    • 题目
    • 分析
      • 题意转换
      • 解题思路
    • 代码实现

欧拉图

定义

• 欧拉回路：通过图中每条边恰好一次的回路
• 欧拉通路：通过图中每条边恰好一次的通路
• 欧拉图：具有欧拉回路的图
• 半欧拉图：具有欧拉通路但不具有欧拉回路的图

性质

欧拉图中所有顶点的度数都是偶数。

若 \(G\) 是欧拉图，则它为若干个环的并，且每条边被包含在奇数个环内。

判别方法

无向图

• 无向图 \(G\) 是欧拉图，当且仅当：

  • 非零度顶点是连通的

  • 顶点的度数都是偶数

• 无向图 \(G\) 是半欧拉图，当且仅当：

  • 非零度顶点是连通的

  • 恰有 0 或 2 个奇度顶点

有向图

• 有向图 \(D\) 是欧拉图，当且仅当：

  • 非零度顶点是强连通的

  • 每个顶点的入度和出度相等

• 有向图 \(D\) 是半欧拉图，当且仅当：

  • 非零度顶点是弱连通的

  • 至多一个顶点的出度与入度之差为 1

  • 至多一个顶点的入度与出度之差为 1

  • 其他顶点的入度和出度相等

示例

以如下有向图为例

从顶点 1 出发，因为顶点 4 和顶点 5 的入度不等于出度，所以，它不存在欧拉通路。

如下有向图都存在欧拉通路：

求欧拉回路的方法

Fleury 算法

也称避桥法，是一个偏暴力的算法。

算法流程为每次选择下一条边的时候优先选择不是桥的边。

Hierholzer 算法

也称逐步插入回路法。

算法流程为从一条回路开始，每次任取一条目前回路中的点，将其替换为一条简单回路，以此寻找到一条欧拉回路。如果从路开始的话，就可以寻找到一条欧拉路。

实现

Hierholzer 算法的暴力实现如下：

\[\begin{array}{ll} 1 & \textbf{Input. } \text{The edges of the graph } e , \text{ where each element in } e \text{ is } (u, v) \\ 2 & \textbf{Output. } \text{The vertex of the Euler Road of the input graph}.\\ 3 & \textbf{Method. } \\ 4 & \textbf{Function } \text{Hierholzer } (v) \\ 5 & \qquad circle \gets \text{Find a Circle in } e \text{ Begin with } v \\ 6 & \qquad \textbf{if } circle=\varnothing \\ 7 & \qquad\qquad \textbf{return } v \\ 8 & \qquad e \gets e-circle \\ 9 & \qquad \textbf{for} \text{ each } v \in circle \\ 10& \qquad\qquad v \gets \text{Hierholzer}(v) \\ 11& \qquad \textbf{return } circle \\ 12& \textbf{Endfunction}\\ 13& \textbf{return } \text{Hierholzer}(\text{any vertex}) \end{array} \]

性质

这个算法的时间复杂度约为 \(O(nm+m^2)\)。实际上还有复杂度更低的实现方法，就是将找回路的 \(DFS\) 和 \(Hierholzer\) 算法的递归合并，边找回路边使用 Hierholzer 算法。

如果需要输出字典序最小的欧拉路或欧拉回路的话，因为需要将边排序，时间复杂度是 \(\Theta(n+m\log m)\)（计数排序或者基数排序可以优化至 \(\Theta(n+m)\)。

如果不需要排序，时间复杂度是 \(\Theta(n+m)\)。

应用

计算机译码

设有 \(m\) 个字母，希望构造一个有 \(m^n\) 个扇形的圆盘，每个圆盘上放一个字母，使得圆盘上每连续 \(n\) 位对应长为 \(n\) 的符号串。转动一周（\(m^n\) 次）后得到由 \(m\) 个字母产生的长度为 \(n\) 的 \(m^n\) 个各不相同的符号串。

构造如下有向欧拉图：

设 \(S = \{a_1, a_2, \cdots, a_m\}\)，构造 \(D=\langle V, E\rangle\)，如下：

\[\begin{aligned} V = & \{a_{i_1}a_{i_2} \cdots a_{i_{n-1}} \ | \ a_i \in S, 1 \leq i \leq n - 1 \} \\ E = & \{a_{j_1}a_{j_2} \cdots a_{j_{n-1}} \ | \ a_j \in S, 1 \leq j \leq n\} \end{aligned} \]

规定 \(D\) 中顶点与边的关联关系如下：

顶点 \(a_{i_1} a_{i_2} \cdots a_{i_{n-1}}\) 引出 \(m\) 条边：

\[a_{i_1}a_{i_2}\cdots a_{i_{n-1}}a_r, \ r=1, 2, \cdots, m \]

边 \(a_{j_1}a_{j_2}\cdots a_{j_{n-1}}\) 引入顶点

\[a_{j_2}a_{j_3}\cdots a_{j_{n}} \]

这样的 \(D\) 是连通的，且每个顶点入度等于出度（均等于 \(m\)），所以 \(D\) 是有向欧拉图。

任求 \(D\) 中一条欧拉回路 \(C\)，取 \(C\) 中各边的最后一个字母，按各边在 \(C\) 中的顺序排成圆形放在圆盘上即可。

应用

应用1：洛谷 P2731 骑马修栅栏

题目

洛谷 P2731 骑马修栅栏

给定一张有 \(500\) 个顶点的无向图，求这张图的一条欧拉路或欧拉回路。如果有多组解，输出最小的那一组。
在本题中，欧拉路或欧拉回路不需要经过所有顶点。
边的数量 \(m\) 满足 \(1\leq m \leq 1024\)。

解题思路

用 Fleury 算法解决本题的时候只需要再贪心就好，不过由于复杂度不对，还是换 Hierholzer 算法吧。

保存答案可以使用 stack，因为如果找的不是回路的话必须将那一部分放在最后。

注意，不能使用邻接矩阵存图，否则时间复杂度会退化为 \(\Theta(nm)\)。由于需要将边排序，建议使用前向星或者 \(vector\) 存图。

代码实现

#include <algorithm>
#include <cstdio>
#include <stack>
#include <vector>
using namespace std;

struct edge {
  int to;
  bool exists;
  int revref;

  bool operator<(const edge& b) const { return to < b.to; }
};

vector<edge> beg[505];
int cnt[505];

const int dn = 500;
stack<int> ans;

void Hierholzer(int x) {  // 关键函数
  for (int& i = cnt[x]; i < (int)beg[x].size();) {
    if (beg[x][i].exists) {
      edge e = beg[x][i];
      beg[x][i].exists = 0;
      beg[e.to][e.revref].exists = 0;
      ++i;
      Hierholzer(e.to);
    } else {
      ++i;
    }
  }
  ans.push(x);
}

int deg[505];
int reftop[505];

int main() {
  for (int i = 1; i <= dn; ++i) {
    beg[i].reserve(1050);  // vector 用 reserve 避免动态分配空间，加快速度
  }

  int m;
  scanf("%d", &m);
  for (int i = 1; i <= m; ++i) {
    int a, b;
    scanf("%d%d", &a, &b);
    beg[a].push_back((edge){b, 1, 0});
    beg[b].push_back((edge){a, 1, 0});
    ++deg[a];
    ++deg[b];
  }

  for (int i = 1; i <= dn; ++i) {
    if (!beg[i].empty()) {
      sort(beg[i].begin(), beg[i].end());  // 为了要按字典序贪心，必须排序
    }
  }

  for (int i = 1; i <= dn; ++i) {
    for (int j = 0; j < (int)beg[i].size(); ++j) {
      beg[i][j].revref = reftop[beg[i][j].to]++;
    }
  }

  int bv = 0;
  for (int i = 1; i <= dn; ++i) {
    if (!deg[bv] && deg[i]) {
      bv = i;
    } else if (!(deg[bv] & 1) && (deg[i] & 1)) {
      bv = i;
    }
  }

  Hierholzer(bv);

  while (!ans.empty()) {
    printf("%d\n", ans.top());
    ans.pop();
  }
}

应用2：Leetcode 753. 破解保险箱

题目

753. 破解保险箱

有一个需要密码才能打开的保险箱。密码是 \(n\) 位数, 密码的每一位都是范围 \([0, k - 1]\) 中的一个数字。
保险箱有一种特殊的密码校验方法，你可以随意输入密码序列，保险箱会自动记住 最后 \(n\) 位输入 ，如果匹配，则能够打开保险箱。
在只知道密码位数 \(n\) 和范围边界 \(k\) 的前提下，请你找出并返回确保在输入的 某个时刻 能够打开保险箱的任一 最短 密码序列。

用例：

输入：n = 2, k = 2
输出："01100"
注意，"01100"、"10011" 和 "11001" 也可以确保打开保险箱。

解题思路

题意转换

求出一个最短的字符串，使其包含从 $0 \sim k^n $ （ \(k\) 进制）中的所有数字。

思路

将所有的 \(n−1\) 位数作为有向图的节点，共有 \(k^{n - 1}\) 个节点，每个节点有 \(k\) 条入边和出边。

如果某个节点对应的数字为 \(a_1a_2 \cdots a_{n-1}\)，那么，它的第 \(x\) 条出边就连向数字 \(a_2 \cdots a_{n-1} x\) 对应的节点。这样，这样我们从一个节点顺着第 \(x\) 条边走到另一个节点，就相当于输入了数字 \(x\)。

我们以用例 \(n=3,k=2\) 为例，其节点为：“\(00\)”，“\(01\)”，“\(10\)”，“\(11\)”，每个节点有 \(2\) 条边，节点上添加数字 \(0∼1\) 可转化到自身或另一个节点，如下图所示。

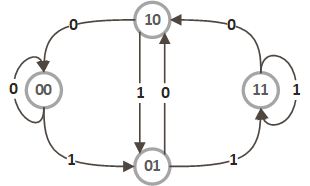
如果我们从任一节点出发，能够找出一条路径，经过图中的所有边且只经过一次，然后把边上的数字写入字符串（还需加入起始节点的数字），那么这个字符串显然符合要求，而且找不出比它更短的字符串了。

Hierholzer 算法

由于这个有向图的每个节点都有 \(k\) 条入边和出边，因此它一定存在一个欧拉回路，即可以从任意一个节点开始，一次性不重复地走完所有的边且回到该节点。

因此，我们可以用 Hierholzer 算法找出这条欧拉回路，这里，我们假设起始节点对应的数为 \(u\)，欧拉回路中每条边的编号为：

\[x_1, x_2, x_3, \cdots \]

那么，最终的字符串为：

\[u x_1 x_2 x_3 \cdots \]

算法的思路如下：

• 从节点 \(u\) 开始，任意地经过还未经过的边，直到我们「无路可走」。

  此时我们一定回到了节点 \(u\)，这是因为所有节点的入度和出度都相等。

  \[u \to \cdots \to v \to \cdots \to u \]

  回到节点 \(u\) 之后，我们得到了一条从 \(u\) 开始到 \(u\) 结束的回路，这条回路上仍然有些节点 \(v\) 有未经过的出边。

• 我们从节点 \(v\) 开始，继续得到一条从 \(v\) 开始到 \(v\) 结束的回路，再嵌入之前的回路中，即

  \[u \to \cdots \to v \to \cdots \to v \to \cdots \to u \]

  以此类推，直到没有节点有未经过的出边，此时我们就找到了一条欧拉回路。

算法步骤：

• 使用深度优先的方式遍历有向图，从起始节点 "\(00\cdots0\)" 出发，遍历它邻近的 \(k\) 个节点；

  假设当前节点为 \(u\)，节点 \(u\) 的出边连接的节点为 \(v\)，那么：

  \[v = u * 10 + x, \{x | 0 \ge x \ge k - 1 \} \]

• 使用 \(path\) 记录访问过的边，已经访问过的节点不再重复访问；

  注意，下一个节点只需要取后 \(n - 1\) 位即可。

• 在路径上添加最后的结束点 \(end\)，结束节点就是起始节点。

这里，我们使用一个集合 \(visited\) 记录访问过的节点，由于会涉及到多次重复访问，使用后序遍历的方式记录访问的路径。

代码实现

class Solution:
    def crackSafe(self, n: int, k: int) -> str:
        visited = set()
        path = list()

        highest = 10 ** (n - 1)
        # 从节点 "00...0"开始遍历
        self.dfs(k, 0, visited, path, highest)
        # 添加结束节点，结束节点就是起点
        path.append("0" * (n - 1))
        return "".join(path)

    def dfs(self, k, node: int, visited, path, highest):
        # 遍历当前节点的邻居节点
        for i in range(k):
            neighboor = node * 10 + i
            if neighboor not in visited:
                visited.add(neighboor)
                # 下一个节点最多取后 n-1 位即可
                self.dfs(k, neighboor % highest, visited, path, highest)
                # 后序遍历记录路径
                path.append(str(i))
        return

class Solution {
    TreeSet<String> visited;
    StringBuilder path;
    public String crackSafe(int n, int k) {
        if(n == 1 && k == 1) {
            return "0";
        }
        visited = new TreeSet<>();
        path = new StringBuilder();
        //  从顶点 00..0 开始
        String start = String.join("", Collections.nCopies(n - 1, "0"));;
        findEuler(start, k);

        path.append(start); // 回路添加最后的 end 顶点，end 就是 start
        return path.toString(); // return new String(path);
    }

    public void findEuler(String curv, int k) {
        for(int i = 0; i < k; i ++) {
            // 往顶点的 k 条出边检查，顶点加一条出边就是一种密码可能
            String nextv = curv + i;
            if(!visited.contains(nextv)) {
                visited.add(nextv);
                findEuler(nextv.substring(1), k);
                path.append(i);
            }
        }
    }
}

应用3：Leetcode 332. 重新安排行程

题目

332. 重新安排行程

分析

题意转换

给定一个 n 个点 m 条边的图，要求从指定的顶点出发，经过所有的边恰好一次（可以理解为给定起点的「一笔画」问题），使得路径的字典序最小。

解题思路

因为本题保证至少存在一种合理的路径，也就告诉了我们，这张图是一个欧拉图或者半欧拉图。我们只需要输出这条欧拉通路的路径即可。

Hierholzer 算法用于在连通图中寻找欧拉路径，其流程如下：

• 从起点出发，进行深度优先搜索。

• 每次沿着某条边从某个顶点移动到另外一个顶点的时候，都需要删除这条边。

• 如果没有可移动的路径，则将所在节点加入到栈中，并返回。

代码实现

class Solution:
    def findItinerary(self, tickets: List[List[str]]) -> List[str]:
        vec = collections.defaultdict(list)
        for depart, arrive in tickets:
            vec[depart].append(arrive)
        for key in vec:
            heapq.heapify(vec[key])

        stack = list()
        self.dfs("JFK", vec, stack)
        return stack[::-1]

    def dfs(self, curr: str, vec, stack):
        while vec[curr]:
            tmp = heapq.heappop(vec[curr])
            self.dfs(tmp, vec, stack)
        stack.append(curr)

---

参考：

• 欧拉通路/欧拉回路

• 欧拉图

• 一步一步推导出 0ms 解法（贪心构造）

• 破解保险箱

• 欧拉路径和Hierholzer算法

• Hierholzer算法