【动态规划】压缩状态
状态压缩动态规划
状态压缩动态规划(BitMask DP),指的是一类使用二进制(也有使用三进制等的情形)数来表示动态规划中的状态的动态规划方法。其时间复杂度一般包含 \(2^N\) 或者 \(3^N\)(如果进行了子集枚举)的项,因此是指数而非多项式时间的算法。
力扣上涉及的题目如下:
| 序号 | 题目 |
|---|---|
| 1 | 465. 最优账单平衡 |
| 2 | 464. 我能赢吗 |
| 3 | 691. 贴纸拼词 |
| 4 | 864. 获取所有钥匙的最短路径 |
应用
应用1:Leetcode.465
题目
给你一个表示交易的数组 transactions ,其中 \(transactions[i] = [from_i, to_i, amount_i]\) 表示 \(ID = from_i\) 的人给 \(ID = to_i\) 的人共计 \(amount_i\) 元钱 。请你计算并返回还清所有债务的最小交易笔数。
示例 1:
输入:transactions = [[0,1,10],[2,0,5]]
输出:2
示例 2:
输入:transactions = [[0,1,10],[1,0,1],[1,2,5],[2,0,5]]
输出:1
解题思路
枚举子集
这道题,需要用到枚举子集的思路,具体的做法,就是用一个整数 \(x\) 的二进制位表示一个集合,其中 \(x\) 的二进制位为 \(1\) 的比特位表示含有对应元素,为 \(0\) 则表示不含有元素,那么,我们可以依次遍历所有的二进制位来枚举 \(x\) 的子集,即:
for (int i = 1; i < (1 << n); ++i) {
for (int j = i; j; j = (j - 1) & i) {
// ...
}
}
其中,j = (j - 1) & i 表示 \(i\) 的 \(LSB\) (最低有效位),注意,这种方式需要采用逆序遍历。
分析
首先将所有的交易数据做一次预处理,记录每一个用户的最终的账单 \(acounts\),账单金额可能是正,也可能是负。
如果最终的账单金额为正,则表示收益,如果最终的账单金额为负,则表示负债。
在交易过程中,有些用户可能最终的账单为 \(0\),表示经过一系列交易之后,即用户不负债也无受益,那么,该用户就可以不用再参与额外的交易就已经完成平账,因此,我们可以首先过滤掉这一部分用户。
对于剩下的账单金额不为零的用户,我们将其账单金额 \(bill[i]\) 定义为一个集合 \(S\) ,我们可以对集合 \(S\) 分组,将其拆分多个成和为零的子集,然后,通过累加所有子集的交易次数,就可以得到账单集合 \(S\) 的最优还债次数。
例如,\(S = \{4, -1, -1, -1, -1, 6, -6\}\),那么:
我们可以将这些用户分为两组:\(S_1 = \{4, -1, -1, -1, -1\}\),\(S_2 = \{6, -6\}\),其中,\(S_1\) 可以通过 \(5 - 1 = 4\) 次交易完成平账,\(S_1\)可以通过 \(2 - 1 = 1\) 次交易完成平账,那么,集合 \(S\) 就可以通过 \(5\) 次交易完成平账。
注意,这里 \(S_1\) 和 \(S_2\) 互为补集。
结论:也就是说,假如一个账单集合 \(S_i\) 的和为零,那么,它最多可以通过 \(i - 1\) 次交易完成平账。
这里,我们用二进制数 \(m\) 表示账单集合 \(S\),即 \(m\) 的二进制位为 1 时,表示选择 \(bill[i]\) 参与当前集合 \(S_i\) 的平账。然后,我们需要计算集合 \(S\) 的每一个的子集 \(S_i\) 对应的交易金额的和 \(sum[i]\)。
对于子集 \(S_i\) 的交易金额之和 \(sum[i]\),一定满足如下关系:
其中,\(\oplus\) 表示异或运算,\(i \oplus (1 << j)\) 表示 \(j\) 的补集。\(i\ \&\ (1 << j)\) 表示集合 \(i\) 的二进制数的LSB。
因此,我们可以从小到大枚举 \(m\) 的子集 \(i\),并计算的所有子集 \(i\) 的交易金额之和。由于我们是从小到大枚举,因此,\(j\) 的补集 \(\complement_ij\) 对应的交易金额之和 \(sum[i \oplus (1 << j)]\) 一定已经计算过了。
动态规划
我们假设 \(i\) 个用户的账单集合为 \(S_i\),其中, \(S_i[k] \ne 0\),同时,假设 \(dp[i]\) 表示的集合 \(S_i\) 所需要的最优还债次数。
边界条件
容易得出,当集合中的元素个数为零时,交易次数为零,因此,边界条件:
状态转移
通过观察,可以总结出以下结论:
-
如果集合 \(S_i\) 中所有元素之和不为零,那么
集合 \(S_i\) 所有用户无法通过交易平账,所以,我们将其置为正无穷,即 \(dp[i] = \infty\);
-
如果集合 \(S_i\) 中所有元素之和为零,那么
集合 \(S_i\) 中所有元素,最多可以通过 \(\operatorname{binCount}(i) - 1\) 次操作,完成平账。因此,我们可以通过枚举集合 \(S_i\) 所有的子集 \(S_j\) 及其对应的补集 \(S_{i-j}\) ,找到它们的交易次数最少的一个组合,就是最优的交易次数,即
\[dp[i] = \min(i - 1, \min^i_{j=0}(dp[S_j] + dp[S_{i-j}])) \]
综上,状态转移方程:
其中, \(\operatorname{binCount}(i)\) 表示 \(i\) 的二进制数中的 \(1\) 的个数。
因此,当集合中的元素个数为 \(n\) 时,平账所需要的次数就是 \(dp[2 ^ n - 1]\)。
代码
class Solution:
def minTransfers(self, transactions: List[List[int]]) -> int:
acounts = defaultdict(int)
for transaction in transactions:
acounts[transaction[0]] += transaction[2]
acounts[transaction[1]] -= transaction[2]
bill = list()
for _, account in acounts.items():
if account:
bill.append(account)
n = len(bill)
m = 1 << n # 总的状态数
_sum = [0] * m
# 枚举所有的状态,计算当前分组的交易金额的总和
for i in range(1, m):
# 枚举状态i的子集j
for j in range(n):
if i & (1 << j):
_sum[i] = _sum[i ^ (1 << j)] + bill[j] # i ^ (1 << j) 表示补集
break
dp = [0] * m
# 枚举所有的状态
for i in range(1, m):
if _sum[i]:
dp[i] = float("INF")
else:
dp[i] = bin(i).count("1") - 1
# 从最低有效位开始枚举所有的子集,找到最少的交易次数
j = (i - 1) & i
while j > 0:
dp[i] = min(dp[i], dp[j] + dp[i ^ j])
j = (j - 1) & i
return dp[m - 1]
应用2:Leetcode.464
题目
在 "100 game" 这个游戏中,两名玩家轮流选择从 1 到 10 的任意整数,累计整数和,先使得累计整数和 达到或超过 100 的玩家,即为胜者。如果我们将游戏规则改为 “玩家 不能 重复使用整数” 呢?
例如,两个玩家可以轮流从公共整数池中抽取从 1 到 15 的整数(不放回),直到累计整数和 >= 100。
给定两个整数 maxChoosableInteger (整数池中可选择的最大数)和 desiredTotal(累计和),若先出手的玩家能稳赢则返回 true ,否则返回 false 。假设两位玩家游戏时都表现 最佳 。
示例 1:
输入:maxChoosableInteger = 10, desiredTotal = 11
输出:false
解释:
无论第一个玩家选择哪个整数,他都会失败。
第一个玩家可以选择从 1 到 10 的整数。
如果第一个玩家选择 1,那么第二个玩家只能选择从 2 到 10 的整数。
第二个玩家可以通过选择整数 10(那么累积和为 11 >= desiredTotal),从而取得胜利.
同样地,第一个玩家选择任意其他整数,第二个玩家都会赢。
示例 2:
输入:maxChoosableInteger = 10, desiredTotal = 0
输出:true
解题思路
注意,题目中的累计整数和表示两位选手选择的数字之和,所以,我们只需要枚举所有的选择顺序。
状态压缩
假设最大可选择的数字为 \(n\),我们考虑边界条件,当所有的数字都选择之后,其和 \(S\) 都小于 \(desiredTotal\),那么,先手一定不能获胜,即
由于 \(n\) 最大值为 \(20\),因此,我们可以用一个 \(4\) 字节(\(20 \le 32\))的整数 \(state\) 记录所有的状态。
我们假设 \(state\) 中的第 \(i\) 个二进制位为 \(1\) 则表示这个数字已经使用过了,为 \(0\) 则表示没有使用过。使用过一个二进制数之后,将该位置为 \(1\)。
我们采用自顶向下的方式枚举所有的状态,这里,我们定义一个函数:
boolean dfs(int n, int state, int desiredTotal, int currentTotal)
用于表示从未选择的数字中,选择一个数字,如果能获胜,则返回 \(true\),否则返回 \(false\),其中,\(state\) 用于记录所有的状态,\(currentTotal\) 表示当前的选择的数字之和。
算法的思路:
- 枚举所有先手玩家可能选择的数字,并用 \(state\) 记录每一个已经选择过的数字;
- 对于每一个没有选择过的数字,判断对于当前玩家选择最优解是否能获胜,若选择的数字与当前的累计整数和相加大于\(desiredTotal\),则当前玩家一定能获胜;
- 否则,继续判断对手从剩余数字中选择,选择一个数字,判断对手是否有最优解,如果对手不能赢,则先手玩家一定获胜;
由于遍历过程中,会存在很多重复状态,这里通过一个备忘录 \(memory\) 记录已经计算过的状态结果。
代码
- Java实现
class Solution {
private Map<Integer, Boolean> memory = new HashMap<>();
public boolean canIWin(int maxChoosableInteger, int desiredTotal) {
if ((1 + maxChoosableInteger) * maxChoosableInteger / 2 < desiredTotal) {
return false;
}
return dfs(maxChoosableInteger, 0, desiredTotal, 0);
}
private boolean dfs(int n, int state, int desiredTotal, int currentTotal) {
if (!memory.containsKey(state)) {
boolean result = false;
// 枚举先手所有可能选择的数字
for (int i = 0; i < n; i++) {
// 选择一个没有使用过的数字
if (((state >> i) & 1 ) == 0 ) {
// 对于当前选手他会选择的最优解,如果累计和已经大于目标值,则当前选手能获胜
if (i + 1 + currentTotal >= desiredTotal) {
result = true;
break;
}
// 对手从选择剩余的数字中选择,是否会赢,如果对手不能赢,则返回先手获胜
if (!dfs(n, state | (1 << i), desiredTotal, currentTotal + i + 1)) {
result = true;
break;
}
}
}
memory.put(state, result);
}
return memory.get(state);
}
}
- Python实现
from functools import cache
class Solution:
def canIWin(self, maxChoosableInteger: int, desiredTotal: int) -> bool:
@cache
def dfs(usedNumbers: int, currentTotal: int) -> bool:
for i in range(maxChoosableInteger):
if (usedNumbers >> i) & 1 == 0:
if currentTotal + i + 1 >= desiredTotal or not dfs(usedNumbers | (1 << i), currentTotal + i + 1):
return True
return False
return (1 + maxChoosableInteger) * maxChoosableInteger // 2 >= desiredTotal and dfs(0, 0)
应用3:Leetcode.691
题目
解题思路
假设目标字符串 \(target\) 的长度为 \(m\),对于字符串的每一个位置都选择和不选择两种策略,那么,它共有 \(2^m\) 个子序列 \(S_i\)。
我们可以将目标字符串将其分解为子问题,即,拼凑出某个子序列 \(S_i\) 所需要的最少贴纸数,又可以由 \(S_i\) 的子序列来递归计算。
这里,我们定义一个函数:
int dp(String [] stickers, String target, int[] memory, int state)
用于表示不同状态所需要的最小贴纸数量,其中,\(state\) 表示字符串 \(target\) 某一个子序列。
我们用 \(state\) 的二进制位记录选择的状态,即,如果 \(state\) 的第 \(i\) 个二进制位为 \(1\),则表示选择字符串 \(target\) 的第 \(i\) 个字符,如果为 \(0\),则表示不选择。
在计算过程中,我们需要选择最优的单词 \(sticker\),让它贡献部分字符,未被 \(sticker\) 覆盖的剩余字符,需要通过递归调用继续求解子问题。
我们假设初始状态为 \(state = (1 << m) - 1 = 111\cdots111\),即表示所有的字符都选择了。
对于贴纸上的每一个单词:
- 我们首先计算该单词 \(sticker\) 中每个字符出现的次数;
- 遍历目标子序列中未使用过的字符,如果该字符在单词 \(sticker\) 中出现次数大于零,则将出现次数减一,并将当前状态 \(left\) 求补集;
- 如果该单词 \(sticker\) 对目标子序列有贡献,则继续求解子问题;
代码实现
class Solution {
public int minStickers(String[] stickers, String target) {
int m = target.length();
int [] memory = new int[1 << m];
Arrays.fill(memory, -1);
// 空字符串所需贴纸的数量为零
memory[0] = 0;
int result = dp(stickers, target, memory, (1 << m) - 1);
return result <= m ? result : -1;
}
private int dp(String [] stickers, String target, int[] memory, int state) {
int m = target.length();
// 没有计算过的状态
if (memory[state] < 0){
int result = m + 1;
for (String sticker : stickers) {
int left = state;
int[] count = new int[26];
for (int i = 0; i < sticker.length(); i++) {
count[sticker.charAt(i) - 'a']++;
}
for (int i = 0; i < target.length(); i++) {
char currentChar = target.charAt(i);
if (((state >> i) & 1) == 1 && count[currentChar - 'a'] > 0) {
count[currentChar - 'a']--;
// 计算left的补集
left = left ^ (1 << i);
}
}
// 如果left对目标子序列有贡献,则继续求解剩余的子序列
if (left < state) {
result = Math.min(result, dp(stickers, target, memory, left) + 1);
}
}
memory[state] = result;
}
return memory[state];
}
}
应用3:Leetcode.864
题目
解题思路
我们使用一个整数 \(mask\) 记录获取到钥匙的状态,即,整数 \(mask\) 的每一个二进制位表示获取钥匙的状态:
- 如果整数 \(mask\) 的第 \(i\) 位为 \(1\),则表示获取到第 \(i\) 把钥匙;
- 如果整数 \(mask\) 的第 \(i\) 位为 \(0\),则表示未获取到第 \(i\) 把钥匙;
对于所有的钥匙序号,我们可以对矩阵中的数据做一个预处理,用一个 \(hash\) 表 \(status\) 记录所有的每一个位置的钥匙及其对应的序号。
代码实现
from collections import deque
from typing import List
START = "@"
EMPTY_ROOM = "."
WALL = "#"
DIRECTIONS = [(-1, 0), (1, 0), (0, -1), (0, 1)]
class Solution:
def shortestPathAllKeys(self, grid: List[str]) -> int:
m, n = len(grid), len(grid[0])
start_x = start_y = 0
# 记录每一把钥匙的状态位
status = dict()
count = 0
for i in range(m):
for j in range(n):
# 记录起点的位置
if grid[i][j] == START:
start_x, start_y = i, j
# 如果这个位置是钥匙,并且没有被访问过
elif grid[i][j].islower() and grid[i][j] not in status:
status[grid[i][j]] = count # 记录该钥匙的状态位
count += 1
# 通过广度优先遍历,查找所有钥匙的最短路径,队列中保存每个位置及其状态,起始状态没有钥匙用0表示
q = deque([(start_x, start_y, 0)])
visit = dict() # 记录每个点的步数
visit[(start_x, start_y, 0)] = 0
while q:
_x, _y, mask = q.popleft()
for direction in DIRECTIONS:
# 从起点开始遍历邻近的节点
x, y = _x + direction[0], _y + direction[1]
# 只要下一个点在网格内,并且不是墙,就可以移动
if 0 <= x < m and 0 <= y < n and grid[x][y] != WALL:
# 如果当前位置是空房间或者起点
if grid[x][y] == EMPTY_ROOM or grid[x][y] == START:
# 并且未被访问过,就将这个位置的步数加1,并将其加入队列中
if (x, y, mask) not in visit:
visit[(x, y, mask)] = visit[(_x, _y, mask)] + 1
q.append((x, y, mask))
# 如果当前位置是钥匙
elif grid[x][y].islower():
# 钥匙对应的状态位就是index
index = status[grid[x][y]]
if (x, y, mask | (1 << index)) not in visit:
visit[(x, y, mask | (1 << index))] = visit[(_x, _y, mask)] + 1
# 当所有的二进制位都为1时,表示钥匙收集齐了
if (mask | (1 << index)) == (1 << len(status)) - 1:
return visit[(x, y, mask | (1 << index))]
q.append((x, y, mask | (1 << index)))
# 如果当前位置是锁,对应的锁就是grid[x][y].lower()
else:
# 不可能出现的场景:两次经过了某个房间,并且这两次我们拥有钥匙的情况是完全一致的
if (x, y, mask) in visit:
continue
# 钥匙对应的状态位就是index
index = status[grid[x][y].lower()]
# 该状态位必须是1,即遍历的路径上已经拾取了对应的钥匙,才能通过该位置
if mask & (1 << index):
# 将该位置新的状态对应的步数加1,并将其放入队列
visit[(x, y, mask)] = visit[(_x, _y, mask)] + 1
q.append((x, y, mask))
return -1
应用4:Leetcode.1494
题目
给你一个整数 n 表示某所大学里课程的数目,编号为 1 到 n ,数组 relations 中, relations[i] = [xi, yi] 表示一个先修课的关系,也就是课程 xi 必须在课程 yi 之前上。同时你还有一个整数 k 。
在一个学期中,你 最多 可以同时上 k 门课,前提是这些课的先修课在之前的学期里已经上过了。请你返回上完所有课最少需要多少个学期。题目保证一定存在一种上完所有课的方式。
示例 1:
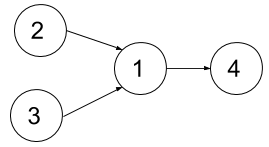
输入:n = 4, relations = [[2,1],[3,1],[1,4]], k = 2
输出:3
解释:上图展示了题目输入的图。在第一个学期中,我们可以上课程 2 和课程 3 。然后第二个学期上课程 1 ,第三个学期上课程 4 。
解题思路
注意,题目中的条件,在上过某些课程的前提下,选出满足约束条件的课程,在本学期可以上的课程需要满足:
-
课程之前没上过;
-
课程的先修课已经全部都上完了。
以题目中的用例为例,假设有 5 门课程,编号为:\(1,2,3,4,5\)。假如第一学期上了课程 \(2\) 和课程 \(3\)(它们没有先修课),那么问题就变成「上完课程 \(1,4,5\) 最少需要多少个学期」,这是一个和原问题相似的子问题,因此我们可以用动态规划求解。
我们用一个整数 \(S\) 来表示当前还需要学习的课程集合,即 \(S\) 的二进制数从低位到高位,第 \(i\) 位为 \(1\) 则表示课程 \(i\) 还需要进行学习,否则表示课程 \(i\) 已经完成学习。
设全集 \(S = \{0, 1, 2, \cdots, n - 1\}\),设 \(prerequisite[i]\) 表示集合 \(i\) 中所有课程的先修课程的并集,特别地,如果没有先修课程,则 \(prerequisite[i] = \emptyset\)。
同时,假设 \(dp[i]\) 表示上完集合 \(i\) 中的课程,最少需要多少个学期。
这里,为了方便状态表示,我们重新对课程进行编号,从 \(0\) 开始编号,即原来编号为 \(x\) 的课程现在为 \(x−1\)。
边界条件
需要上的课程数为零时,不需要任何学期就可以完成,所以,边界条件为:
状态转移
对于每一个课程及其先修课程,我们使用一个二进制的比特位来记录其状态,因此,其状态转移方程为:
其中,\(\oplus\) 表示异或运算,\(i \oplus j\) 表示从集合 \(i\) 中移除 \(j\) 的操作,即 \(i \oplus j = \complement_ij\)。
对于状态 \(i\) 的任意一个子集 \(j\),\(prerequisite[i]\) 表示:子集 \(j\) 的先修课程与子集 \(j\) 的补集 \(\complement_ij\) 的先修课程的并集。
为了方便计算,我们可以从 \(i\) 的 LSB 开始枚举子集 \(j\),即 \(j = i\ \&\ (-i)\),此时,\(i \oplus j = i\ \&\ (i - 1)\)。
此时,状态转移方程 1 等价于:
状态转移过程:
-
我们考虑从小到大枚举集合 \(i\) 的非空子集 \(j\),作为一个学期内要学完的课程;
注意,集合 \(j\) 中的课程数不能超过每学期最多可以上的课程数 \(k\) ,即这里 \(j\) 中的所有元素的先修课程必须都在 \(i\) 的补集 \(\complement_Si\) 中,表示前面学期已经学完了 \(j\) 中的所有课程的先修课,即 \(prerequisite[i] \subseteq \complement_Si\)。
-
当 \(j\) 满足如下条件时,我们就可以学习课程 \(j\):
-
\(j\) 的大小不能超过每学期最多可以上的课程数 \(k\);
-
剩下课程集合 \(i\oplus j\) 为可以在有限的学期内完成学习;
即 \(dp[i \oplus j] \ne +\infty\)。
-
剩下课程集合 \(i\oplus j\) 中不存在 \(j\) 的先修课程。
即 \(prerequisite[j]\ \&\ i \oplus j = prerequisite[j]\)。
-
-
否则,\(dp[i]\) 仍然为 \(+\infty\)。
因此,我们可以从小到大枚举每一个状态 \(i\) 的 \(prerequisite[i]\) 和 \(dp[i]\),最后完成 \(n\) 门课程需要的最少学期数就为 \(dp[2^n -1]\)。
代码实现
from typing import List
class Solution:
def minNumberOfSemesters(self, n: int, relations: List[List[int]], k: int) -> int:
max_state = (1 << n)
dp = [float("INF")] * max_state
# prerequisite[1] = 0110 表示1的先修课为2和3
prerequisite = [0] * max_state
for relation in relations:
prerequisite[(1 << (relation[1] - 1))] |= 1 << (relation[0] - 1)
dp[0] = 0
# taken表示已经上过的课,假设taken = 0111,表示课程1 2 3已经上过了
for taken in range(1, max_state):
prerequisite[taken] = prerequisite[taken & (taken - 1)] | prerequisite[taken & (-taken)]
# taken 中有任意一门课程的前置课程没有完成学习
if (prerequisite[taken] | taken) != taken:
continue
# 当前学期可以进行学习的课程集合
current = taken ^ prerequisite[taken]
# 如果个数小于 k,则可以全部学习,不再枚举子集
if current.bit_count() <= k:
dp[taken] = min(dp[taken], dp[taken ^ current] + 1)
else:
# 枚举子集
sub_mask = current
while sub_mask:
if sub_mask.bit_count() <= k:
dp[taken] = min(dp[taken], dp[taken ^ sub_mask] + 1)
sub_mask = (sub_mask - 1) & current
return int(dp[-1])
参考:


 浙公网安备 33010602011771号
浙公网安备 33010602011771号