【动态规划】矩阵

矩阵

矩阵相关的典型应用如下：

序号	题目
1	174. 地下城游戏
2	562. 矩阵中最长的连续1线段

应用

应用1：Leetcode.174

题目

174. 地下城游戏

分析

省略。

代码实现

class Solution:
    def uniquePaths(self, m: int, n: int) -> int:
        dp = [[0 for _ in range(n)] for _ in range(m)]

        for i in range(m):
            dp[i][0] = 1

        for i in range(n):
            dp[0][i] = 1

        for i in range(1, m):
            for j in range(1, n):
                dp[i][j] = dp[i - 1][j] + dp[i][j - 1]
        return dp[m - 1][n - 1]

应用2：Leetcode.562

题目

562. 矩阵中最长的连续1线段

解题思路

动态规划

假设 \(dp[i][j][k]\) 表示以位置 \((i-1,\ j-1)\) 结尾的某个方向上最长的连续 \(1\) 的个数，其中，\(k = 0,1,2,3\)，分别表示向右、向右下、向下、向左下方向，即：

• \(dp[i][j][0]\)：以 \((i, j)\) 结尾的水平线段最长 \(1\) 的线段长度；
• \(dp[i][j][1]\)：以 \((i, j)\) 结尾的主对角线段最长 \(1\) 的线段长度；
• \(dp[i][j][2]\)：以 \((i, j)\) 结尾的垂直线段最长 \(1\) 的线段长度；
• \(dp[i][j][3]\)：以 \((i, j)\) 结尾的反对角线段最长 \(1\) 的线段长度；

注意，状态 \(dp[i][j][k]\) 对应的位置为 \(mat[i - 1][j - 1]\)。

边界条件

当矩形大小为零时，最长 \(1\) 的线段长度为零，即

\[\begin{aligned} dp[0][j][k] = 0, \ k \in \{0,1,2,3\} \\ dp[i][0][k] = 0, \ k \in \{0,1,2,3\} \end{aligned} \]

状态转移

考虑从左上往右下遍历矩阵，对于 \(dp[i][j][k]\) ，它可以通过前面已经计算出得状态转移而来，\(dp\) 矩阵如下图所示：

因此，对于 \(dp[i][j][k]\)，存在两种情况：

• 如果当前位置 \(mat[i - 1][j - 1]\) 的值为 \(1\)，那么，存在如下状态转移过程：

\[\begin{aligned} dp[i][j][0] &= dp[i][j - 1][0] + 1 \\ dp[i][j][1] &= dp[i - 1][j - 1][1] + 1 \\ dp[i][j][2] &= dp[i - 1][j][2] + 1 \\ dp[i][j][3] &= dp[i - 1][j + 1][3] + 1 \\ \end{aligned} \]

• 如果当前位置 \(mat[i - 1][j - 1]\) 的值为 \(0\)，那么，以\(mat[i - 1][j - 1]\) 结尾的线段长度都是 \(0\)，即

\[dp[i][j][k] = 0, \ k \in \{0,1,2,3\} \]

假设矩阵的大小为 \(m \times n\)，为了避免讨论边界条件，我们将 \(dp\) 数组的大小设置为 \((m + 2) \times (n + 2)\)。

我们以下面的矩阵为例，介绍转移过程：

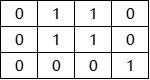
其状态转移过程如下：

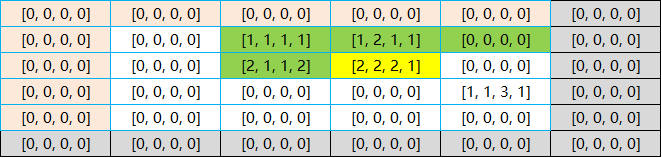
因为我们是从左上向右下遍历矩阵，因此，图中的 \(dp[2][3]\) 的状态，就可以由 \(dp[1][2]\)、\(dp[1][3]\)、\(dp[1][4]\) 和 \(dp[2][2]\) 转移而来。

代码

class Solution:
    def longestLine(self, mat: List[List[int]]) -> int:
        m, n = len(mat), len(mat[0])
        dp = [[ [0] * 4 for _ in range(n + 2)] for _ in range(m + 2)]

        result = 0
        for i in range(1, m + 1):
            for j in range(1, n + 1):
                if mat[i - 1][j - 1] == 1:
                    dp[i][j][0] = dp[i][j - 1][0] + 1
                    dp[i][j][1] = dp[i - 1][j - 1][1] + 1
                    dp[i][j][2] = dp[i - 1][j][2] + 1
                    dp[i][j][3] = dp[i - 1][j + 1][3] + 1
                    result = max(result, dp[i][j][0], dp[i][j][1], dp[i][j][2], dp[i][j][3])
        return result