前缀和的应用 I
简介
求区间和,一般的思路都是利用前缀和的思想。
应用
应用1:Leetcode.303
题目
分析
题目就可以转换为已知数组 \(nums\) ,先求前缀和 \(preSum\) ,然后再求区间和:
代码实现
class NumArray {
private int [] prefixSum;
public NumArray(int[] nums) {
prefixSum = new int[nums.length];
prefixSum[0] = nums[0];
for (int i = 1; i < nums.length; i++) {
prefixSum[i] = prefixSum[i - 1] + nums[i];
}
}
public int sumRange(int left, int right) {
int start = 0;
if (left > 0) {
start = prefixSum[left - 1];
}
return prefixSum[right] - start;
}
}
应用2:Leetcode.523
题目
给你一个整数数组 nums 和一个整数 k ,编写一个函数来判断该数组是否含有同时满足下述条件的连续子数组:
子数组大小 至少为 2 ,且子数组元素总和为 k 的倍数。
如果存在,返回 true ;否则,返回 false 。
如果存在一个整数 n ,令整数 x 符合 x = n * k ,则称 x 是 k 的一个倍数。0 始终视为 k 的一个倍数。
示例 2:
输入:nums = [23,2,6,4,7], k = 6
输出:true
解释:[23, 2, 6, 4, 7] 是大小为 5 的子数组,并且和为 42 。 42 是 6 的倍数,因为 42 = 7 * 6 且 7 是一个整数。
分析
设 \(preSum[i]\) 是数组 \(nums\) 的前缀和。
根据题目的条件,就可以转换为,求满足\((preSum[i] - preSum[j])\ \%\ k\ =\ 0\) 的 \((i,\ j)\) 共有多少对。
根据同余定理,若 \((preSum[i] - preSum[j])\ \%\ k\ =\ 0\) ,那么一定有:
因此,只需要计算每个下标对应的前缀和除以 \(k\) 的余数即可,使用哈希表存储每个余数第一次出现的下标。
算法步骤
因为题目中要求 \(0\) 也是 \(k\) 的倍数,因此,我们规定空的前缀和的结束下标为 \(−1\),由于空的前缀和的元素和为 \(0\),所以,提前在哈希表中存入键值对 \((0, −1)\)。
对于 \(0 \le i\),从小到大依次遍历每个 \(i\),计算每个下标对应的前缀和除以 \(k\) 的余数,并维护哈希表:
-
如果当前余数在哈希表中已经存在,则取出该余数在哈希表中对应的下标 \(prevIndex\),\(nums\) 从下标 \(prevIndex + 1\) 到下标 \(i\) 的子数组的长度为 \(i−prevIndex\),该子数组的元素和为 \(k\) 的倍数,如果 \(i−prevIndex \ge 2\),则找到了一个大小至少为 \(2\) 且元素和为 \(k\) 的倍数的子数组,返回 true;
-
如果当前余数在哈希表中不存在,则将当前余数和当前下标 \(i\) 的键值对存入哈希表中。
由于哈希表存储的是每个余数第一次出现的下标,因此当遇到重复的余数时,根据当前下标和哈希表中存储的下标计算得到的子数组长度是以当前下标结尾的子数组中满足元素和为 \(k\) 的倍数的子数组长度中的最大值。只要最大长度至少为 \(2\),即存在符合要求的子数组。
代码实现
【python】
class Solution:
def checkSubarraySum(self, nums: List[int], k: int) -> bool:
n = len(nums)
if n < 2:
return False
pre_sum = [0] * n
pre_sum[0] = nums[0]
for i in range(1, n):
pre_sum[i] = pre_sum[i - 1] + nums[i]
mod_2_index = dict({0: -1})
for i in range(len(pre_sum)):
mod = pre_sum[i] % k
if mod not in mod_2_index:
mod_2_index[mod] = i
else:
if i - mod_2_index.get(mod) >= 2:
return True
return False
【java】
class Solution {
public boolean checkSubarraySum(int[] nums, int k) {
int n = nums.length;
int[] sum = new int[n + 1];
for (int i = 1; i <= n; i++) {
sum[i] = sum[i - 1] + nums[i - 1];
}
Set<Integer> set = new HashSet<>();
for (int i = 2; i <= n; i++) {
set.add(sum[i - 2] % k);
if (set.contains(sum[i] % k)) {
return true;
}
}
return false;
}
}
应用3:Leetcode.304
题目
分析
先求二维矩阵的前缀和
我们定义一个二维矩阵的前缀和 \(sum[i][j]\),表示从原点 \((0,\ 0)\) 至\((i,\ j)\) 的子矩阵的所有数字之和。
任意子矩阵的和
由于我们在遍历矩阵时,按从左向右、从上到下的顺序遍历的,所以,任意子矩阵的前缀和的公式如下:
为了避免讨论边界条件,我们将 \(sum[0][j]\) 和 \(sum[i][0]\) 初始化为 \(0\) 。
以题中的用例为例,原始矩阵如下:
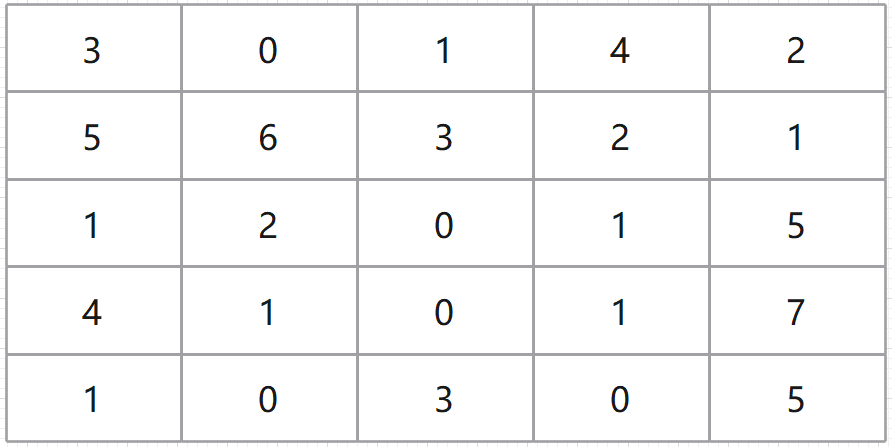
对应地,其前缀和矩阵如下:
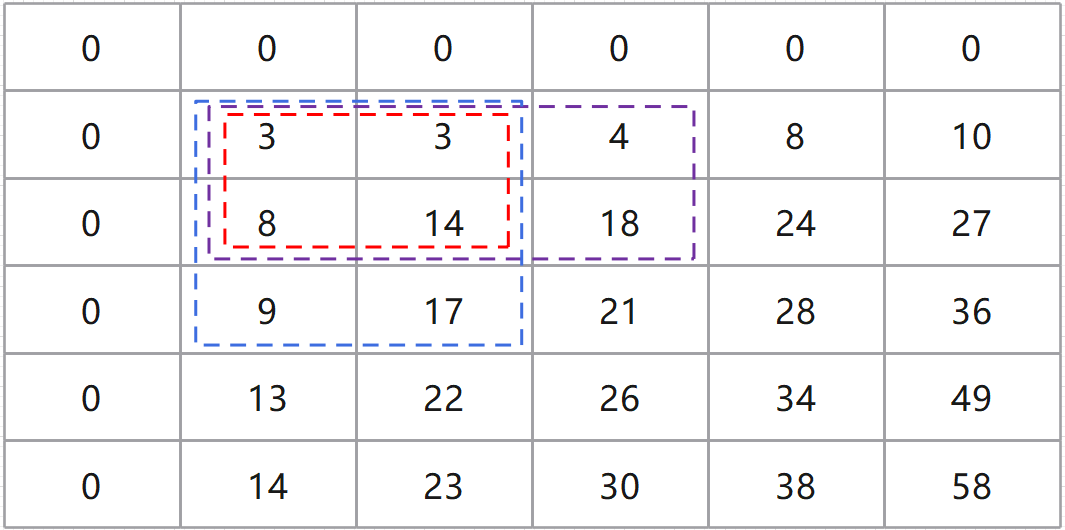
代码实现
class NumMatrix:
def __init__(self, matrix: List[List[int]]):
m, n = len(matrix), (len(matrix[0]) if matrix else 0)
self.sums = [[0] * (n + 1) for _ in range(m + 1)]
for i in range(1, m + 1):
for j in range(1, n + 1):
self.sums[i][j] = self.sums[i - 1][j] + self.sums[i][j - 1] - self.sums[i - 1][j - 1] \
+ matrix[i - 1][j - 1]
def sumRegion(self, row1: int, col1: int, row2: int, col2: int) -> int:
return self.sums[row2 + 1][col2 + 1] - self.sums[row1][col2 + 1] - self.sums[row2 + 1][col1] \
+ self.sums[row1][col1]
应用4:Leetcode.974
题目
分析
方法一
设数组的前 \(n\) 项和为 \(P_n\) ,即:
假设 \(S_{ij}\) 表示任意子数组 \(num[i]\),... ,\(num[j]\) 的和,那么:
如果子数组的和能被 k 整除,那么,就有
根据同模定理,有
因此,对于 \(M\) 有两种情况:
-
如果 \(M = 0\) 时,此时前缀和 \(P_n\) 刚好能被 \(k\) 整除,即使只有一个前缀和能被 \(k\) 整除,也是一种子数组,它不需要与其他的前缀和进行两两组合;
-
如果 \(M \ne 0\) 时,我们就可以求出每一个前缀和对 \(k\) 的模值,并用 \(hash\) 表 \(records\) 记录每个模值出现的次数,利用相同模值的前缀和出现的次数,从而得到两两组合的同模值前缀和的组合数,即题目的答案。
这样,问题就转换为求解所有模值相等的前缀和的两两组合数之和。
例如,前缀和对 \(k\) 模值为 \(i\) 的子数组共 \(n\) 个,那么,两两组合的组合数就是 \(\mathrm C_n^2\),由于
即首项为零的序列的前 \(n\) 项和,所以,可以将组合数转化为对相同模值的前缀和的次数求和。
因此,算法的步骤:
-
遍历数组,记录每个元素的前缀和 \(prefixSum\),并对 \(k\) 取模;
-
累加该模值的出现次数,将其作为答案;
-
更新该模值的出现次数。
注意,对于模值 \(M = 0\) 的场景,即子数组 \(num[0]\),... ,\(num[i]\) 的和能被 \(k\) 整除,此时,它不需要与其他子数组成为子数组对,此时,我们需要将 \(hash\) 表的初始条件设置为 \(records[0] = 1\)。
方法二
这里,也可以将所有的前缀和的模值出现次数都计算完成之后,再利用组合数公式计算答案。
具体算法,参考代码实现。
代码实现
方法一
class Solution:
def subarraysDivByK(self, nums: List[int], k: int) -> int:
# 用hash表记录模值出现的次数
records = dict({0: 1})
prefix_sum = 0
result = 0
for num in nums:
# 求出每个元素对应的的前缀和
prefix_sum += num
# 求出每个元素对K的模
mod = prefix_sum % k
# 模值出现的次数
count = records.get(mod, 0)
# 累加次数
result += count
# 更新hash表中保存的次数
records[mod] = count + 1
return result
方法二
class Solution:
def subarraysDivByK(self, nums: List[int], k: int) -> int:
record = {0: 1}
total = 0
for elem in nums:
total += elem
modulus = total % k
record[modulus] = record.get(modulus, 0) + 1
result = 0
for _modulus, _times in record.items():
result += _times * (_times - 1) // 2
return result


 浙公网安备 33010602011771号
浙公网安备 33010602011771号