【数值优化】基础
“数值”优化:设置算法时,要考虑舍入误差。
数值优化问题分类:
- 无约束优化 VS 约束优化
- 线性规划。目标函数和约束函数都是线性的
- 二次规划。目标函数为二次的,约束函数为线性。
- 凸优化。目标函数为凸的,约束函数为线性的。
局部解 VS 全局解
连续 VS 离散
确定 VS 随机
无约束优化问题基础
解的一阶必要条件: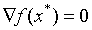
解的二阶必要条件: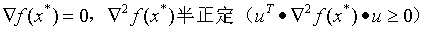
解的二阶充分条件: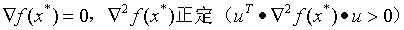
迭代算法(如何构造下一个迭代点)、终止条件
一阶、二阶、直接算法
直接算法无需使用导数,一阶算法需要使用一阶导数,二阶算法需要用到二阶导数。
算法的收敛性:
全局收敛的算法: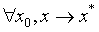
局部收敛的算法: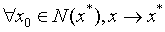
算法收敛速度
线性收敛: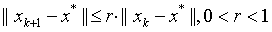
超线性收敛: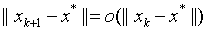
二次收敛: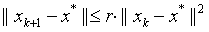
方法概述
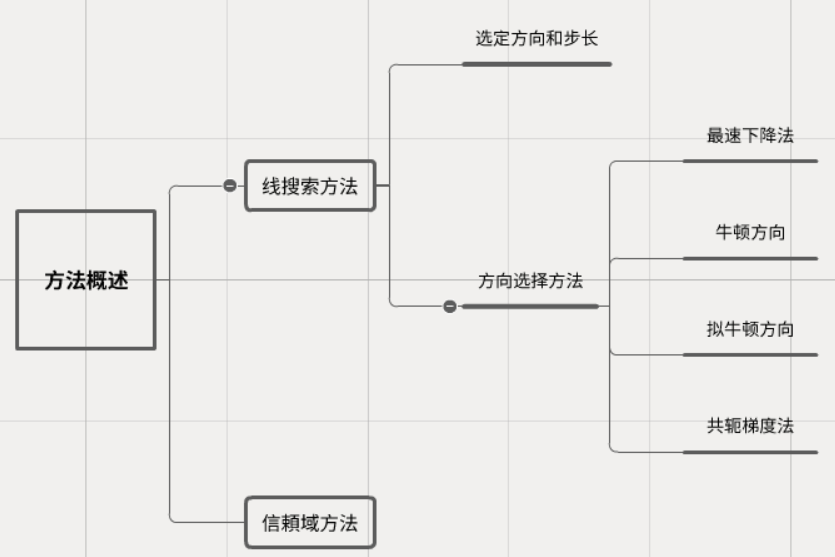

Line Search Method
Line Search Direction
- 最速下降方向(负梯度方向)
- 牛顿方向:二阶近似,要求黑塞矩阵正定
![]()
![]()
- 拟牛顿方向:不需要计算黑塞矩阵,使用一个近似矩阵Bk代替黑塞矩阵
![]()

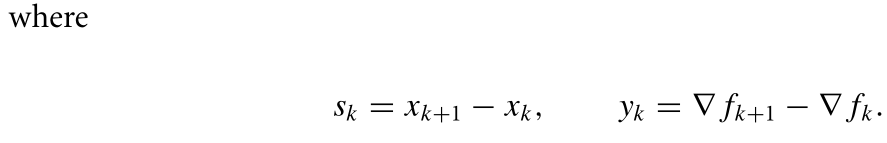
- 共轭梯度方向
![]()
收敛速度
We say that the Q-order of convergence is p if there is a positive constant M such that:

Q-linearly < Q-superlinearly < Q-quadratically <Q-cubic
- Steepest descent method 线性收敛,收敛速度可能很慢
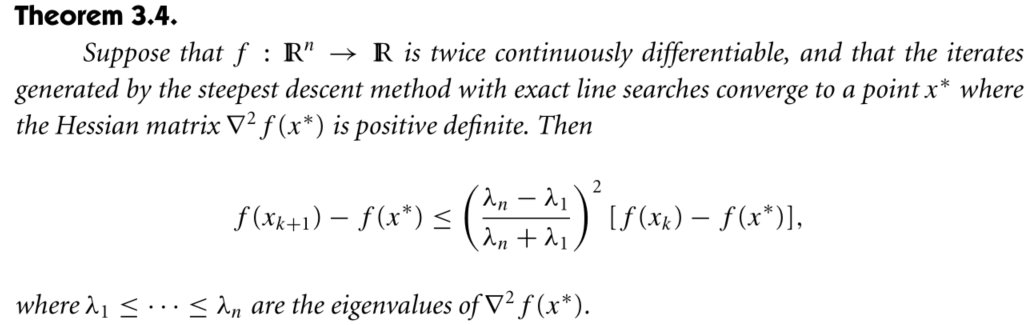
- Quasi-Newton Method 超线性收敛
- Newton Method 二次收敛

步长选择
The step length α should achieves sufficient decrease while preventing α from being too small.
- Wolfe Condition
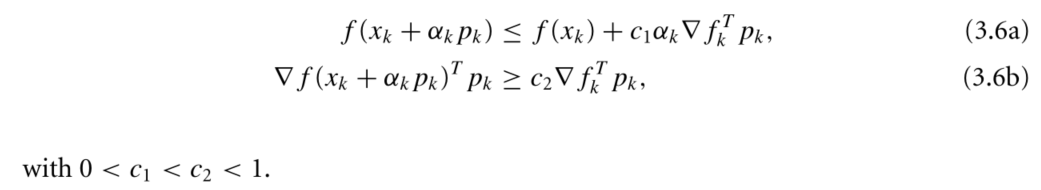
- Strong Wolfe Condition
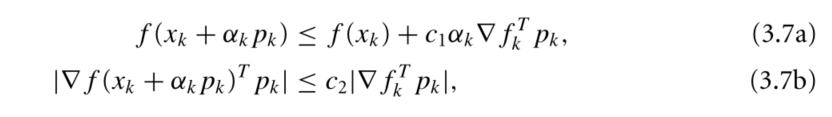
![]()
- Goldstein Condition
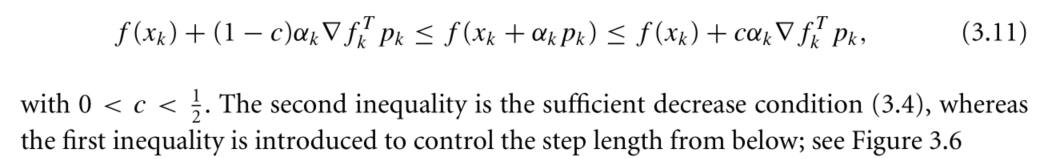
- Backtracking
给定初始步长,按收缩系数逐渐收缩步长,直到满足下降条件:![]()
Trust Region Method
The size of the trust region is crucial to the effectiveness of each step.In practical aogorithms,we choose the size of the region according to the performance of the algorithm during previous iterations.If the model is generally raliable,producing good steps and accurately predicting the behavior of the objective functions,the sie of trust region is increased to allow longer steps to be taken. On the other hand, a fail step indicates the model is an inadequate representation of the objective function over the current region,so we reduce the size of region and try again.
To obtaion each step,we seek a solution of the subproblem:
![]()
We define the ratio:
![]()
If p is close to 1,there is a good agreement between the model mk and the function f over this step,so it is safe to expand the trust region for the next iteration. if p is positive but not close to 1,we do not alter the trust region,but if the p is close to 0 or negative,we shrink the trust region.


Conjugate Gradient Method 共轭梯度法
共轭梯度法是介于最速下降法和牛顿法之间的一个方法,只需要一阶导数信息,但克服了最速下降法收敛慢的缺点,又避免了牛顿法需要存储和计算Hesse矩阵并求逆的缺点,共轭梯度法不仅是解决大型线性方程组最有用的方法之一,也是解大型非线性最优化最有效的算法之一。共轭梯度每一步搜索方向是互相共轭的,搜索方向是负梯度方向和上一步搜索方向的组合,存储量少,计算方便。
The linear conjugate gradient method is an iterative method for solving linear systems with positive definite coefficient matrices. The nonlinear conjugate gradient method is for solving large-scale nonlinear optimization problems,it require no matrix storage and is faster than the steepest descent method.
Linear Conjygate Gradient method

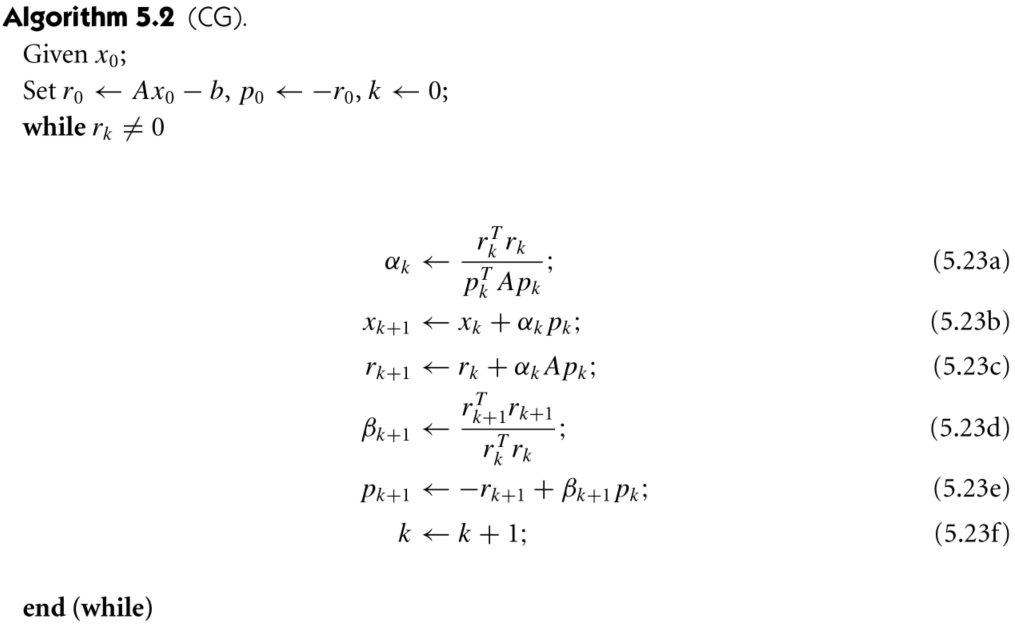
The CG method is recommended only for large problems; otherwise, Gaussian elimination or other factorization algorithms such as the singular value decomposition are to be preferred, since they are less sensitive to rounding errors.
Nonlinear conjugate gradient method
Fletcher-Reeves Method
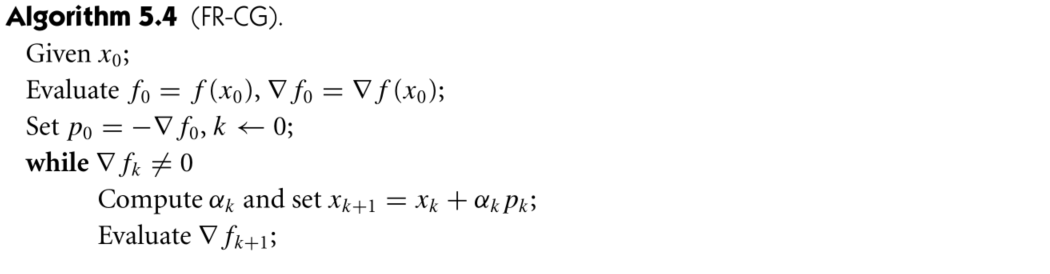
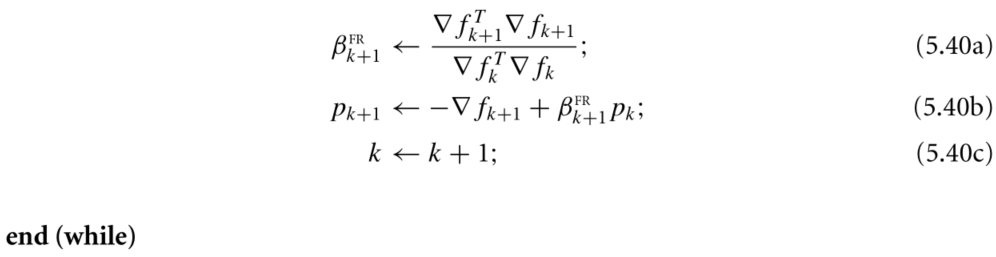
Newton Method
![]()
为保证搜索方向是下降方向,牛顿法要求Hessian矩阵正定,为保证此步长有效,可使用两种方法:1.Newton-CG method,使用共轭梯度法求解步长,遇到负曲率就停止;2.modified Newton Method,修改Hessian矩阵使其变为正定矩阵。
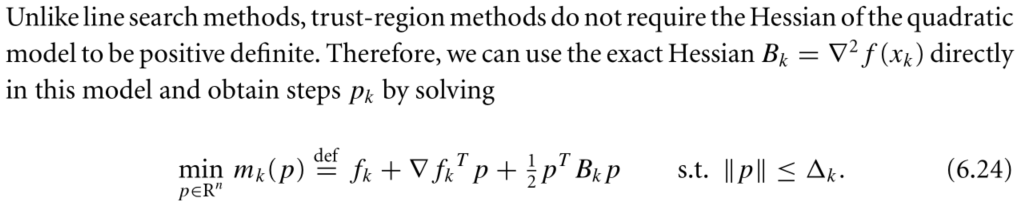
Quasi-Newton Method
拟牛顿法只需要计算一阶导数,不需要计算二阶导数。
BFGS method 秩2更新Bk
![]()
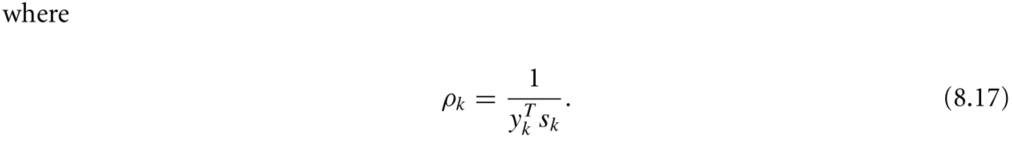

SR1 Method 秩1更新Bk
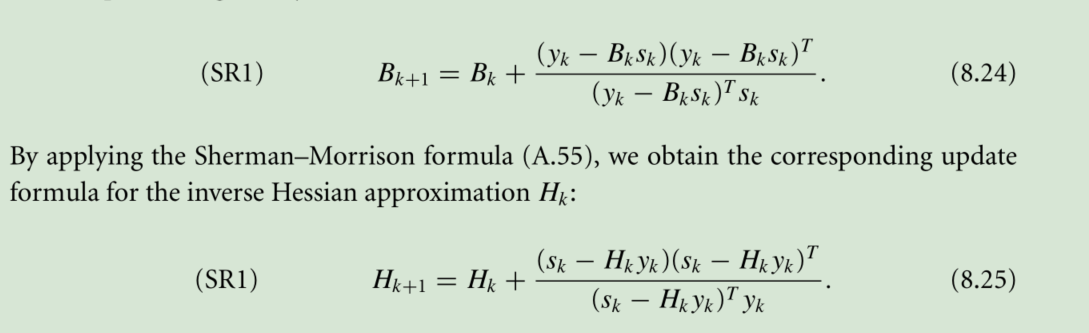
Large Scale Quasi-Newton and Partially Separable Optimization
Limited Memory BFGS
Instead of storing fully dense n × n Hessian matrix approximations, they save just a few vectors of length n that represent the approximations implicitly.
Nonlinear Least-Square Problem
In least square problems,the objective function has the special form:


Gauss-Newton Method
![]()
即解为以下线性最小二乘问题的解:
![]()
即可以使用求解线性最小二乘的方法来求解非线性最小二乘问题的搜索方向,如果使用QR或者SVD算法,则无需显式的计算JTJ
LM Method
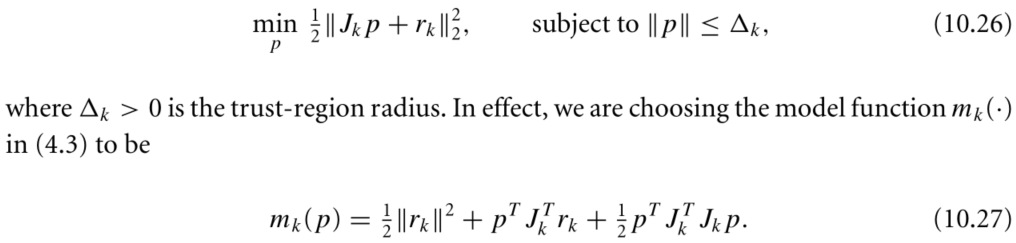

即如果高斯牛顿法的解pGN小于信頼域半径,则pLM=pGN,否则 ||pLM||=信頼域半径。





