径向基函数网络
介绍
径向基函数网络(Radial Basis Function,RBF)是由三层构成的前向网络:第一层为输入层,节点数等于输入的维数;第二层为隐含层,节点个数视问题复杂度而定;第三层为输出层,节点数等于输出数据的维度。RBF的隐含层是非线性的,采用径向基函数作为基函数,从而将输入向量空间转换到隐含层空间,使原来的线性不可分问题变为线性可分,输出层则是线性的。
径向基神经网络可以分为正则化网络和广义网络,在实践中被广泛应用的是广义网络。
正则化网络的隐层节点数等于训练样本数,因此如果训练样本个数N过大,网络的计算量将是惊人的。广义网络隐层选择I个节点,(I<N)
径向基函数
A radial basis function (RBF) is a real-valued function whose value depends only on the distance from the origin, so that


Any function 

由径向基函数的定义可知,函数值仅与自变量的范数有关。范数是对函数、向量和矩阵定义的一种度量形式,只要一种度量形式同时满足以下三个条件,即可成为一种范数:

一个长为n的向量X的p-范数定义为:
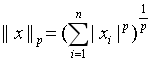
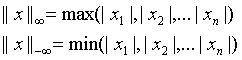
概率神经网络
概率神经网络(Probabilistic Neutral Networks,PNN)可以视为一种径向基神经网络,杂RBF网络的基础上,融合了密度函数估计和贝叶斯决策理论。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号