交叉熵与Softmax

分类问题中，交叉熵常与softmax结合使用，交叉熵能够衡量同一个随机变量中的两个不同概率分布的差异程度，在机器学习中就表示为真实概率分布与预测概率分布之间的差异。交叉熵的值越小，模型预测效果就越好。

交叉熵损失函数Cross Entropy Loss

“信息是用来消除随机不确定性的东西”，信息量大小与信息发生的概率成反比，概率越大，信息量越小；概率越小，信息量越大。

信息量：I(x)=−log(P(x))

信息熵用来表示信息量的期望： 

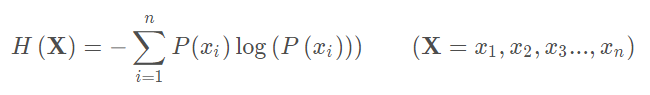
 相对熵（KL散度）

如果对于同一个随机变量X有两个单独的概率分布P(x)和Q(x)，则我们可以使用KL散度来衡量这两个概率分布之间的差异。KL值越小表示两个概率分布更加接近。

 

 交叉熵

 Softmax

Softmax常作为输出层的激励函数，这样输出层的加和为1。

 

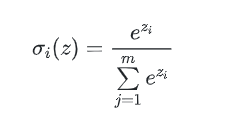
 softmax求导

 

 

 

 即yi-1就是反向更新的梯度。