方差 标准差 协方差
方差
方差用来度量随机变量和其数学期望之间的偏离程度，variance =E[(X-EX)(X-EX)]
标准差和均值的量纲（单位）是一致的，在描述一个波动范围时标准差比方差更方便。
存在一个值为N的分母，其作用为将计算得到的累积偏差进行平均，从而消除数据集大小对计算数据离散程度所产生的影响。不过，使用N所计算得到的方差及标准差只能用来表示该数据集本身(population)的离散程度；如果数据集是某个更大的研究对象的样本(sample)，那么在计算该研究对象的离散程度时，就需要对上述方差公式和标准差公式进行贝塞尔修正，将N替换为N-1：
简单的说，是除以 N 还是 除以 N-1，则要看样本是否全，比如，我要统计全国20岁男性的平均身高，你肯定拿不到全部20岁男性的身高，所以只能随机抽样 500名，这时要除以 N-1，因为只是部分数据（称为整体数据的无偏估计）；但是我们算沪深300在2017年3月份的涨跌幅，我们是可以全部拿到3月份的数据的，所以我们拿到的是全部数据，这时就要除以 N。
协方差
协方差Covariance用于描述2个随机变量偏离其均值的程度，cov(X,Y)=E[(X-EX)(Y-EY)]=E(XY)-E(X)*E(Y)
协方差作为描述X和Y相关程度的方法，在同一物理量纲下有一定的作用。但是两个变量采用不同的量纲时，他们的协方差在数值上会表现出很大的差异。为此引出相关系数的公式（如下），其具有如下特点：
- 相关系数是一个衡量线性独立的无量纲数
- 取值范围是[-1,1]
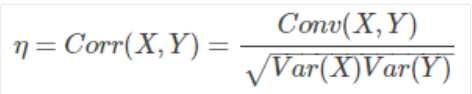
协方差矩阵
协方差矩阵的每个元素是各个向量元素之间的协方差，是从标量随机变量到高维度随机向量的自然推广。协方差矩阵为对称非负定矩阵。
