矩阵分解

QR分解

QR分解（正交三角分解）是将一个矩阵分解为一个正交矩阵Q和上三角矩阵R的乘积 A=QR

解线性方程组 Ax=b

Ax=b-->QRx=b-->x=R\(Q\b)

求特征值

 LU分解

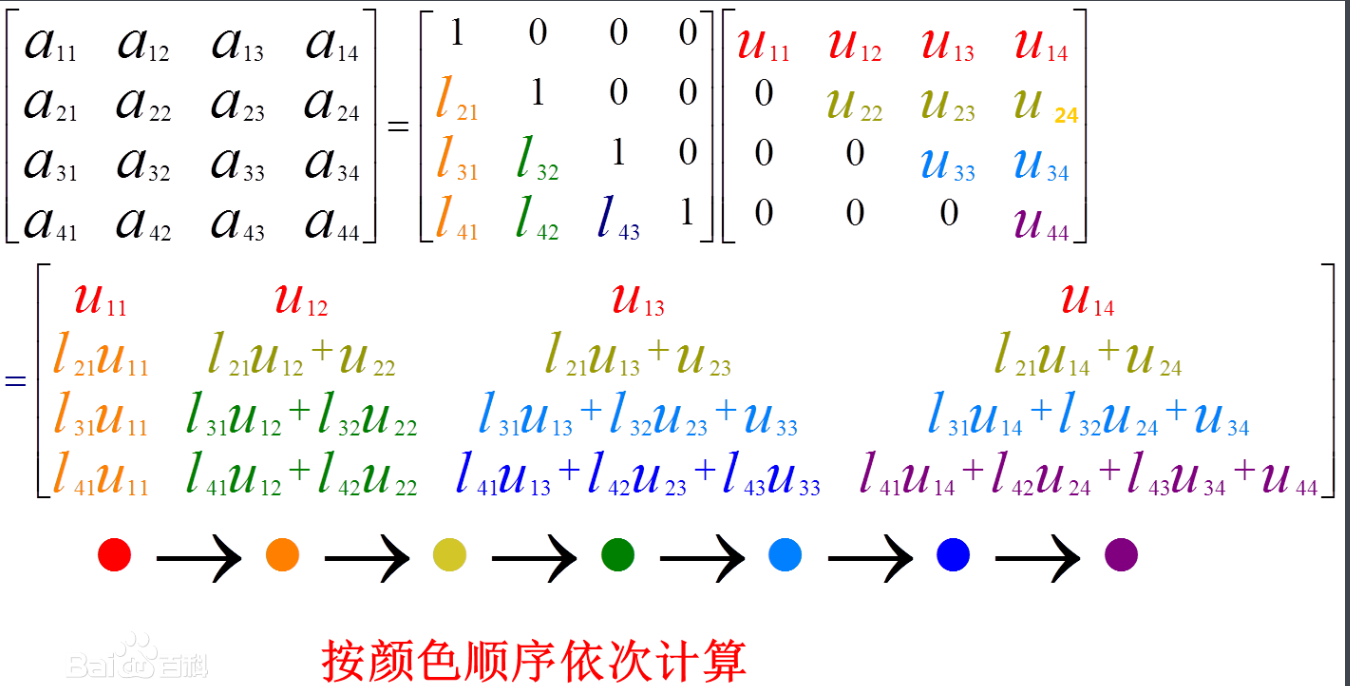
LU分解将一个矩阵分解为一个单位下三角矩阵和一个上三角矩阵的乘积，A=LU

LU分解在本质上是高斯消元法的一种表达形式。实质上是将A通过初等行变换变成一个上三角矩阵，其变换矩阵就是一个单位下三角矩阵。

 SVD分解

参考：

奇异值分解(SVD)原理详解及推导

SVD(Singular Value Decomposition,奇异值）分解，SVD是最可靠的分解法，但是它比QR 分解法要花上近十倍的计算时间。[U,S,V]=svd(A)，其中U和V分别代表两个正交矩阵，而S代表一对角矩阵。 和QR分解法相同， 原矩阵A不必为正方矩阵。使用SVD分解法的用途是解最小平方误差法和数据压缩。

 

 正交矩阵是在欧几里得空间里的叫法，在酉空间里叫酉矩阵，一个正交矩阵对应的变换叫正交变换，正交变换的特点是不改变向量的尺寸和向量间的夹角。

SVD分解：对于任意的M*N矩阵A，找到一组正交基使得经过它变换后还是正交基。A矩阵将n维空间中的向量映射到k维空间中，k=Rank(A)。现在的目标就是：在n维空间中找一组正交基，使得经过A变换后还是正交的。

 Cholesky分解

 Cholesky(乔里斯基)分解把矩阵分解为一个下三角矩阵以及它的共轭转置矩阵的乘积。与一般的矩阵分解求解方程的方法比较，Cholesky分解效率很高。

Cholesky分解条件：

1.Hermitian Matrix:矩阵元素共轭对称。

 2.矩阵正定。

只要矩阵满足以上两个条件，则A=LL* (L*为L的共轭转置矩阵），L唯一确定且L的对角线元素为正数；如果A是半正定的则A也可以分解，只不过这时候L就不唯一了。如果A是实数对称矩阵，那么L的元素肯定也是实数。