视觉里程计VO-特征点法

视觉里程计的主要问题是如何根据图像来估计相机运动，VO的实现方法，按照是否需要提取特征，分为特征点法的前端以及不提取特征的直接法前端。基于特征点法的前端，长久以来被认为是视觉里程计的主流方法，它运行稳定，对光照、动态物体不敏感，是目前较为成熟的解决方案。

计算机视觉邻域的研究者们，设计了许多比角点更加稳定的局部图像特征，比如SIFT,SURF,ORB等。特征点由关键点（Key-point)和描述子（Descriper)两部分组成。SIFT(Scale Invariant Feature Transform 尺度不变特征变换）计算量大，普通 PC 的 CPU还无法实时地计算 SIFT 特征，进行定位与建图。所以在 SLAM 中我们甚少使用这种“奢侈”的图像特征。ORB（Oriented FAST and Rotated BRIEF）特征则是目前看来非常具有代表性的实时图像特征。它改进了 FAST 检测子 不具有方向性的问题，并采用速度极快的二进制描述子BRIEF，使整个图像特征提取的环节大大加速。

根据匹配点对，估计相机运动

1. 当相机为单目时，我们只知道 2D 的像素坐标，因而问题是根据两组 2D 点估计运动。该问题用对极几何来解决。
2. 当相机为双目、RGB-D 时，或者我们通过某种方法得到了距离信息，那问题就是根据两组 3D 点估计运动。该问题通常用 ICP 来解决。
3. 如果我们有 3D 点和它们在相机的投影位置，也能估计相机的运动。该问题通过 PnP求解。

 2D-2D对级几何

 

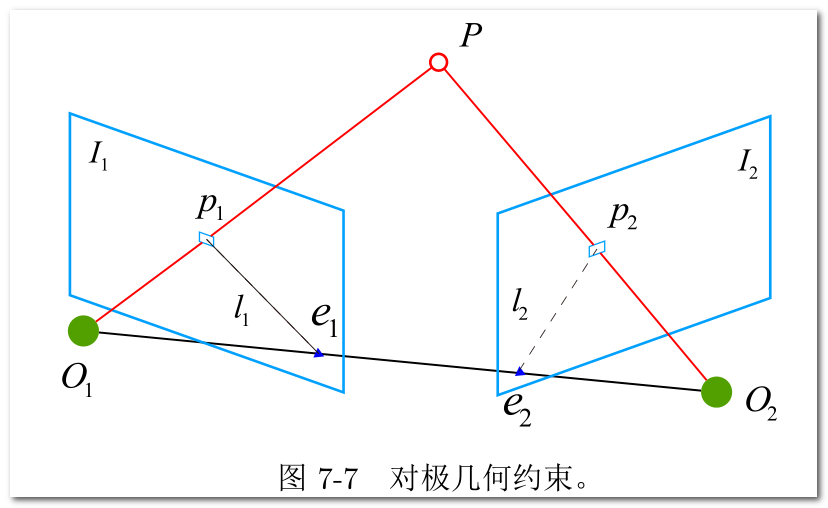
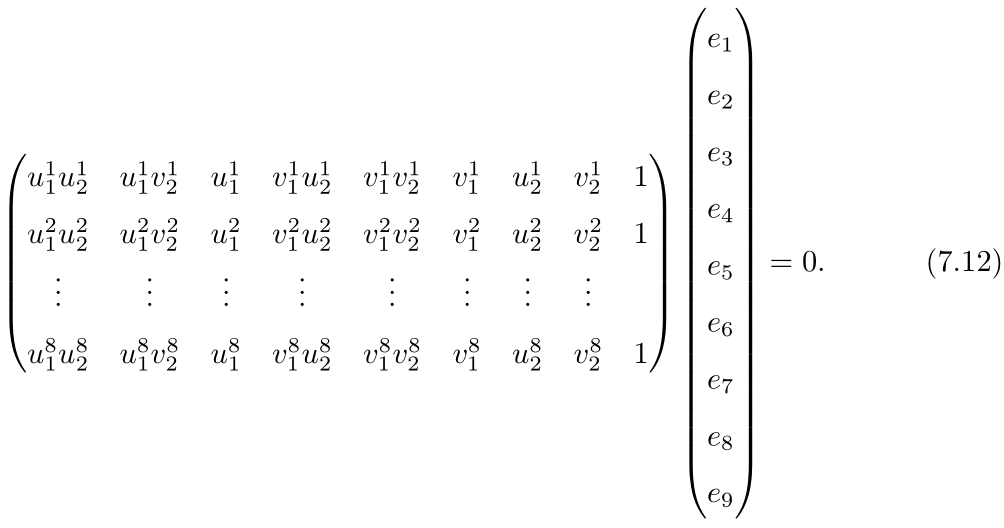
 本质矩阵E由于满足对级约束，所以E满足尺度等价性，矩阵E具有5个自由度，表明我们可以最少使用5对点来计算E矩阵，但是E的内在非线性性质使得求解线性方程时比较麻烦。可使用经典的8点法在线性框架下求解。

 

 

 

 求得E后，根据奇异值分解，恢复相机的R，t

单应矩阵H

单应矩阵描述了两个平面之间的映射关系，如果场景中的特征点都位于同一平面上，则可以通过单应性来进行运动估计。

 openCV相关函数：

findFundamentalMat()　　计算基础矩阵

findEssentialMat（）　　计算本质矩阵

findHomography（）　　计算单应矩阵

recoverPose（）　　从本质矩阵中恢复旋转和平移

triangulatePoints（）　　通过三角化计算空间点位置

3D:2D PnP

PnP(Perspective-n-Point)描述了当我们知道了n个3D空间点以及它们的投影位置时，如何估计相机所在的位姿。PnP不需要使用对极约束，可以在很少的匹配点中获得较好的运动估计，是一种重要的姿态估计方法。

PnP求解有很多求解方法，如仅用三对点估计的P3P，直接线性变换DLT,非线性优化Bundle Adjustment。SLAM中通常的做法是先使用P3P/EPnP等方法估计相机位姿，然后构建最小二乘优化问题对估计值进行调整（Bundle Adjustment）

Bundle Adjustment

Bundle Adjustment是一个最小化重投影误差的问题，同时对位姿和空间点进行优化。

 

  openCV相关函数：

solvePnP()　　Finds an object pose from 3D-2D point correspondences. This function returns the rotation and the translation vectors that transform a 3D point expressed in the object coordinate frame to the camera coordinate frame.

3D-3D ICP

可采用SVD方法以及非线性优化方法