使用Python进行缺角矩形区域的流函数方程求解

 

 [larry-wos原创]

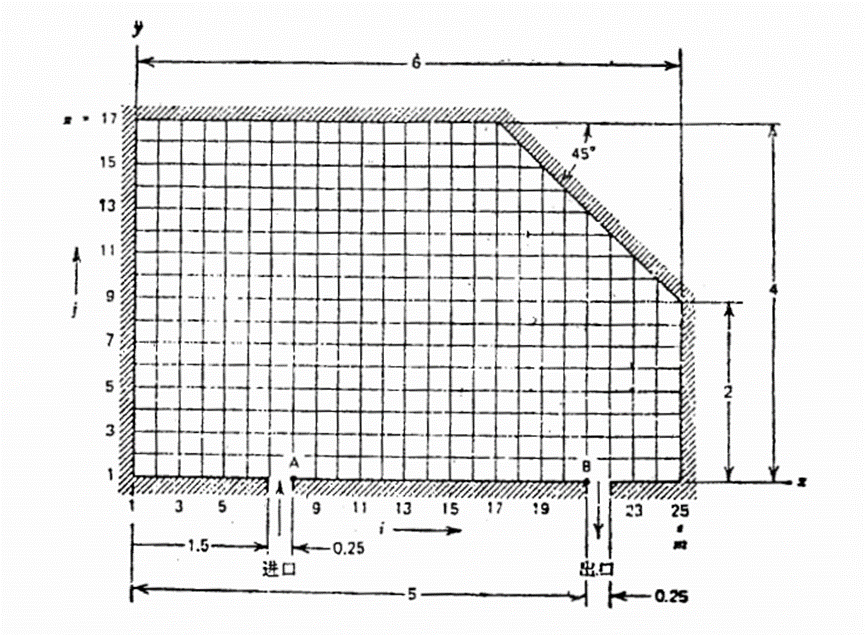该容器为矩形，长度为6，宽度为4，其右上角被一个与轴成45°角的平板所截，位于容器的底壁上有流体的进、出口。流体通过容器流动所形成的流场可近似作为二维流处理。对于容器中的定常流场，其控制方程为：

$$ \frac{{{\partial ^2}\psi }}{{\partial {x^2}}} + \frac{{{\partial ^2}\psi }}{{\partial {y^2}}}{\rm{ }} = 0 $$

对于上述偏微分方程，采用中心差分法来离散方程，得到偏微分方程的离散格式为：

$$\frac{1}{{{{\left( {\Delta {\rm{x}}} \right)}^2}}}\left( {{\psi _{i + 1,j}} - 2{\psi _{i,j}} + {\psi _{i - 1,j}}} \right) + \frac{1}{{{{\left( {\Delta y} \right)}^2}}}\left( {{\psi _{i + 1,j}} - 2{\psi _{i,j}} + {\psi _{i - 1,j}}} \right) = 0$$

由于使用的网格为正方形网格，故上式可变为：

\[{\psi _{i,j}} = \frac{1}{4}\left( {{\psi _{i + 1,j}} + {\psi _{i - 1,j}} + {\psi _{i,j + 1}} + {\psi _{i,j - 1}}} \right)\] 

对上式使用直接法得到的迭代公式为：

\[\psi _{i,j}^{\left( {n + 1} \right)} = \frac{1}{4}\left( {\psi _{i - 1,j}^{\left( n \right)} + \psi _{i + 1,j}^{\left( n \right)} + \psi _{i,j - 1}^{\left( n \right)} + \psi _{i,j + 1}^{\left( n \right)}} \right)\] 

对上式使用逐次超松弛（SOR）方法得到的迭代公式为：

\[\psi _{i,j}^{\left( {n + 1} \right)} = \left( {1 - \omega } \right)\psi _{i,j}^{\left( n \right)} + \frac{\omega }{4}\left( {\psi _{i - 1,j}^{\left( n \right)} + \psi _{i + 1,j}^{\left( n \right)} + \psi _{i,j - 1}^{\left( n \right)} + \psi _{i,j + 1}^{\left( n \right)}} \right)\] 

其中\(\omega\)是松弛因子，\(\omega\)的计算方法如下：

$$\begin{array}{l}
\omega = \frac{{8 - 4\sqrt {4 - {\alpha ^2}} }}{{{\alpha ^2}}}\\
\alpha = \cos \left( {\frac{\pi }{m}} \right) + \cos \left( {\frac{\pi }{n}} \right)
\end{array}$$

\(m,n\)分别表示在划分的网格中垂直线和水平线的总数。本例中，\(m = dx = 25\)，\(n = dy = 17\)。

这是程序中采用的数据插值点的图示：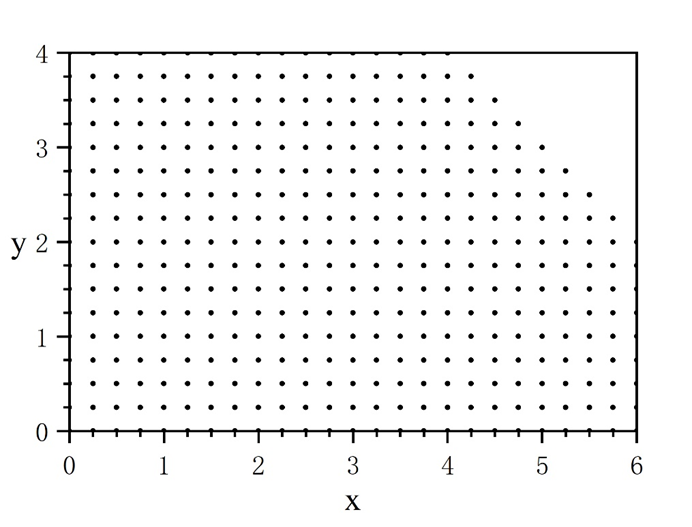

 

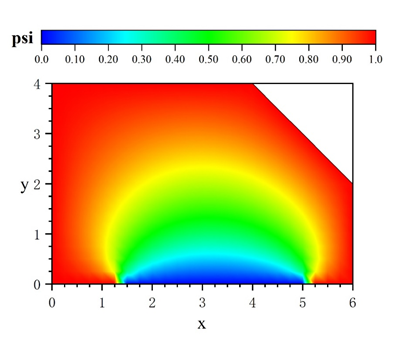
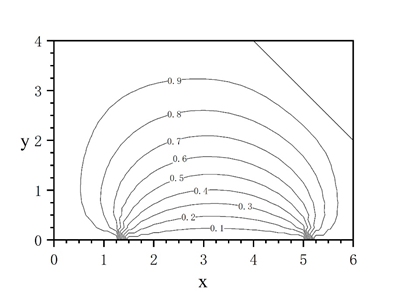
计算所得结果输入到Origin中做势函数云图，势函数云图及势函数等高线图如图所示：

Python所编程序如下，建立插值点及求解过程均包括（对于迭代误差计算的部分不太肯定，但是按照程序所写是可以正常计算的，如有高人，还望指点）。

 

点击查看代码

import numpy
from matplotlib import pyplot
import pandas


nx=25
ny=17
dx=6/(nx-1)
dy=4/(ny-1)
l1norm_target=1e-3
pi=3.1415926535


x= []
y= []
#########
for ylen in numpy.arange(0, 4+dy, dy):
    if ylen<=2:
        xlen=6
        x.append(numpy.linspace(0,xlen,nx))
        y.append(numpy.full((nx),ylen))
    else:
        xlen= 8-ylen
        x.append(numpy.linspace(0,xlen,xlen/dx+1))        #####!!!!!!!!!!
        y.append(numpy.full((int((xlen/dx)+1)),ylen))
##############     


# 所有数据点的x坐标与y坐标

X=[]
for j in range(0,ny):
    if j <= int(2/dx):
        for i in range(0,nx):
            X.append(x[j][i])
    else:
        for i in range(0,int((8-j*dy)/dx+1)):
            X.append(x[j][i])

# print('X = ',X)

Y=[]
for j in range(0,ny):
    if j <= int(2/dx):
        for i in range(0,nx):
            Y.append(y[j][i])
    else:
        for i in range(0,int((8-j*dy)/dx+1)):
            Y.append(y[j][i])

# print('Y = ',Y)


# 定义待求的列表p_larry
p_larry= []

for ylen in numpy.arange(0, 4+dy, dy):
    if ylen<=2:
        xlen=6
        p_larry.append(numpy.zeros(int((xlen/dx)+1)))
    else:
        xlen= 8-ylen
        p_larry.append(numpy.zeros(int((xlen/dx)+1)))
        
# print('p_larry =  ',p_larry)
# print(p_larry[16].shape)


# boundary condition 
for a in range(0,ny):
    p_larry[a][0]= 1
    if a <= int(2/dy):
        p_larry[a][nx-1]= 1
    else:
        p_larry[a][-1]= 1
        
p_larry[ny-1][:]= 1
p_larry[0][0:int(1.5/dx)]= 1
# p_larry[0][int(1.75/dx):int(5/dx)]= 0
p_larry[0][int(5.25/dx):nx]= 1


# 定义alpha以及omega
alpha=numpy.cos(pi/nx)+numpy.cos(pi/ny)
omega=(8-4*((4-alpha**2)**0.5))/(alpha**2)


# 定义计算域的初始场p_larryn
p_larryn=[]
for j in range(0,ny):
    if j <= int(2/dx):
            p_larryn.append(numpy.empty_like(p_larry[j][:]))
    else:
            p_larryn.append(numpy.empty_like(p_larry[j][:]))

# print('p_larry = ',p_larry)
# print('p_larryn = ',p_larryn)    
            

a = 0
b = 0
iteration = 0            


# 使用指定迭代次数的方法
# iteration_target=2000
# while iteration <= iteration_target:

# 使用指定内点上的误差和的方法
residual = 1
residual_target = 1e-3
while residual > residual_target: 
    
    p_larryn = p_larry.copy()
        
    for j in range(1,ny-1):
        for i in range(1,p_larry[j].shape[0]-1):
            p_larry[j][i]=(1-omega)*p_larryn[j][i]+omega*(p_larryn[j][i-1]+p_larryn[j][i+1]+p_larryn[j-1][i]+p_larryn[j+1][i])/4
#             p_larry[j][i] = ((dy**2*(p_larryn[j][i+1]+p_larryn[j][i-1])+dx**2*(p_larryn[j+1][i]+p_larryn[j+1][i]))/(2*(dx**2+dy**2)))
            for a in range(0,ny):
                p_larry[a][0]= 1
                if a <= int(2/dy):
                    p_larry[a][nx-1]= 1
                else:
                    p_larry[a][-1]= 1

            p_larry[ny-1][:]= 1
            p_larry[0][0:int(1.5/dx)]= 1
            p_larry[0][int(1.75/dx):int(5/dx)]= 0
            p_larry[0][int(5.25/dx):nx]= 1
    
# 使用指定内点上的误差和的方法           
        b += numpy.sum(p_larry[j])
        a += numpy.sum(p_larryn[j]) 
    residual = a/(b-a)
    
    
    iteration += 1
    print('number of iteration :', iteration)
    print('residual = ', residual)


# 将计算结果转换到能与数据点的坐标相对应的列表中
P=[]
for j in range(0,ny):
    if j <= int(2/dx):
        for i in range(0,nx):
            P.append(p_larry[j][i])
    else:
        for i in range(0,int((8-j*dy)/dx+1)):
            P.append(p_larry[j][i])

print('P=',P)
print('sum number of iteration :', iteration)
print('the end residual = ', residual)


# 导出计算结果
All = pandas.DataFrame({
    'X': X,
    'Y': Y,
    'P': P
})
All.to_csv("c://users//xxx//Desktop//All.csv", index=False)