Brief Introduction of Bezier Curve and Bspline: B-spline (2)

1.Non-uniform B-spline

上一篇中的B-spline是均匀的uniform，因为每一段Bezier Curve的traverse time都是一样的。那么non-uniform B-spline就是Bezier Curve的traverse time不一样，即表现为knot vector相邻元素之间的差不是1了。例如上一篇中例子的knot vector={0,0,0,0,1,2,3,3,3,3}，如果knot vector变成{0,0,0,0,0.5,2,3,3,3,3}，这就是non-uniform B-spline了。三段Bezier Curve的traverse time分别为[0, 0.5], [0.5, 2], [2, 3]。此时的基函数如下图(右)所示。

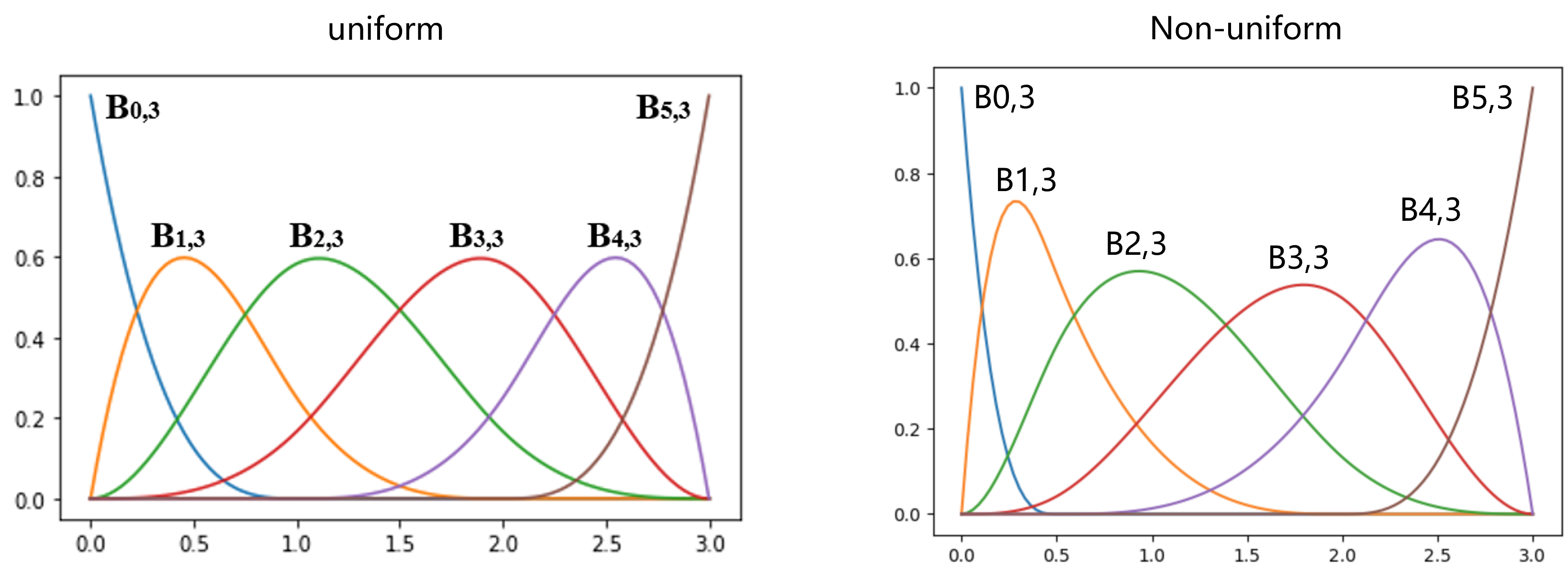
B-spline的对比如下图所示。

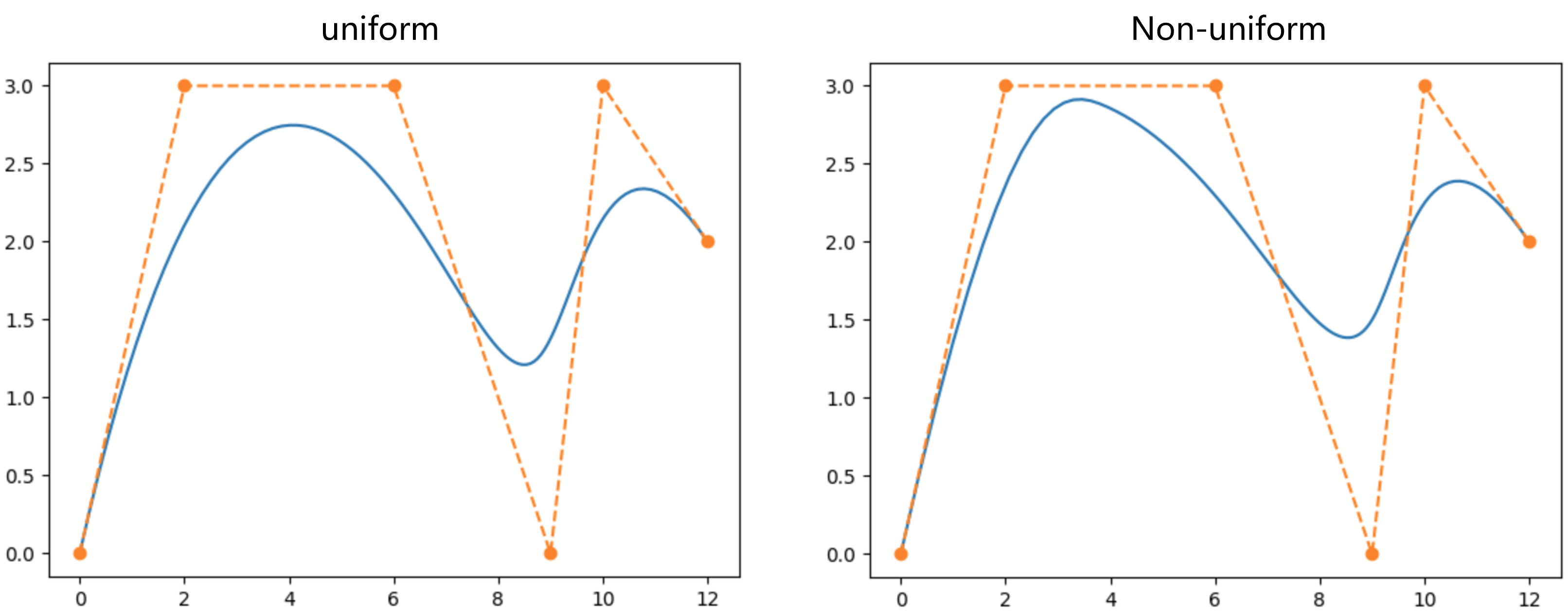
2.B-spline极坐标表达

下图所示为两条Bezier Curve的极坐标表达，第一条$t\in[a,b]$，第二条$t\in[b,c]$。那么两条Bezier Curve达到$C^0$连续的条件为： $$A[b,b,b]=B[b,b,b]\space\space\space(1)$$

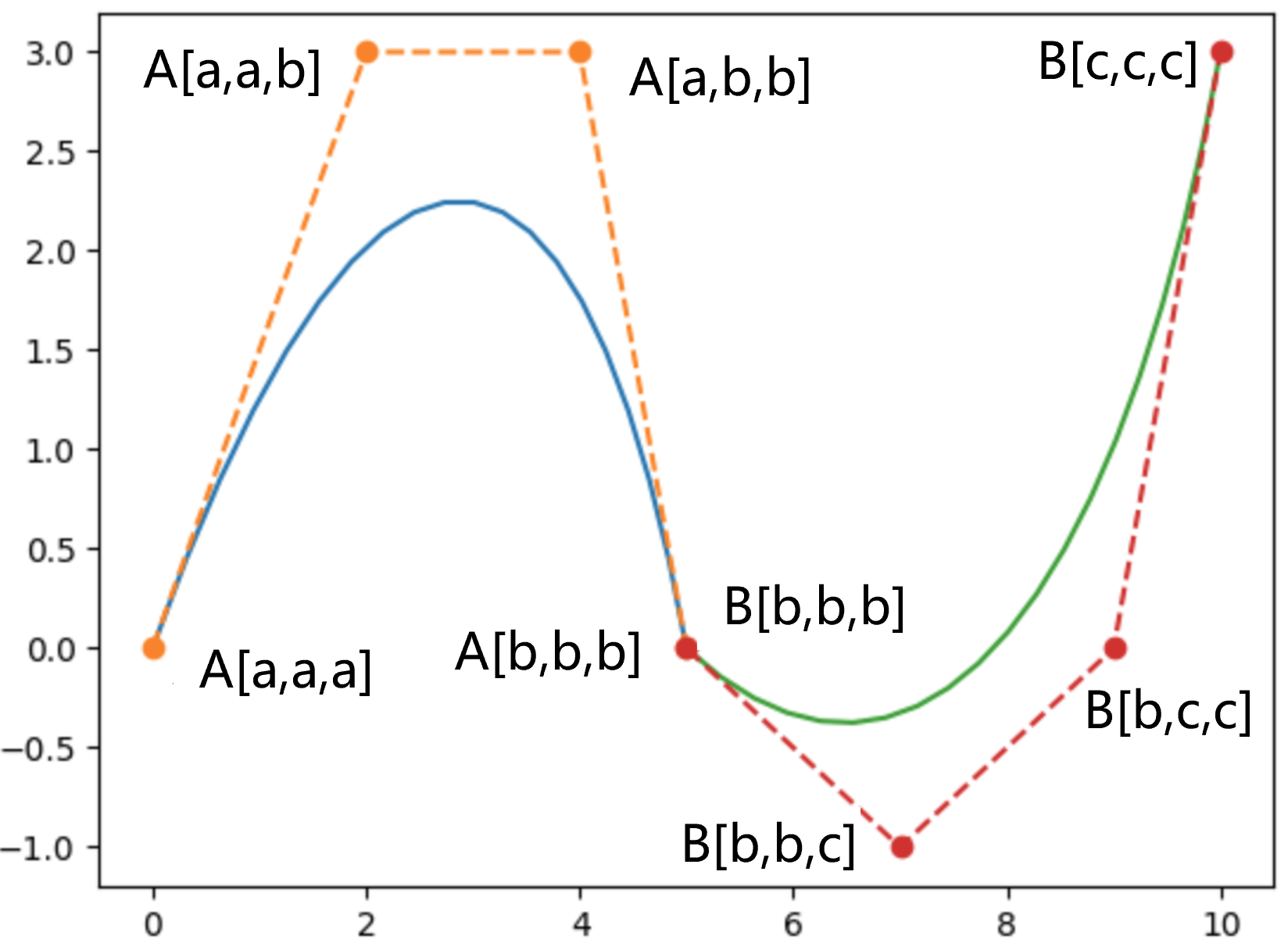
进一步地，如下图所示，达到$C^1$连续的条件为： $$ \begin{array}{l} A[a,b,b]=B[b,b,a]\\ A[c,b,b]=B[b,b,c] \end{array}\space\space\space(2) $$

 

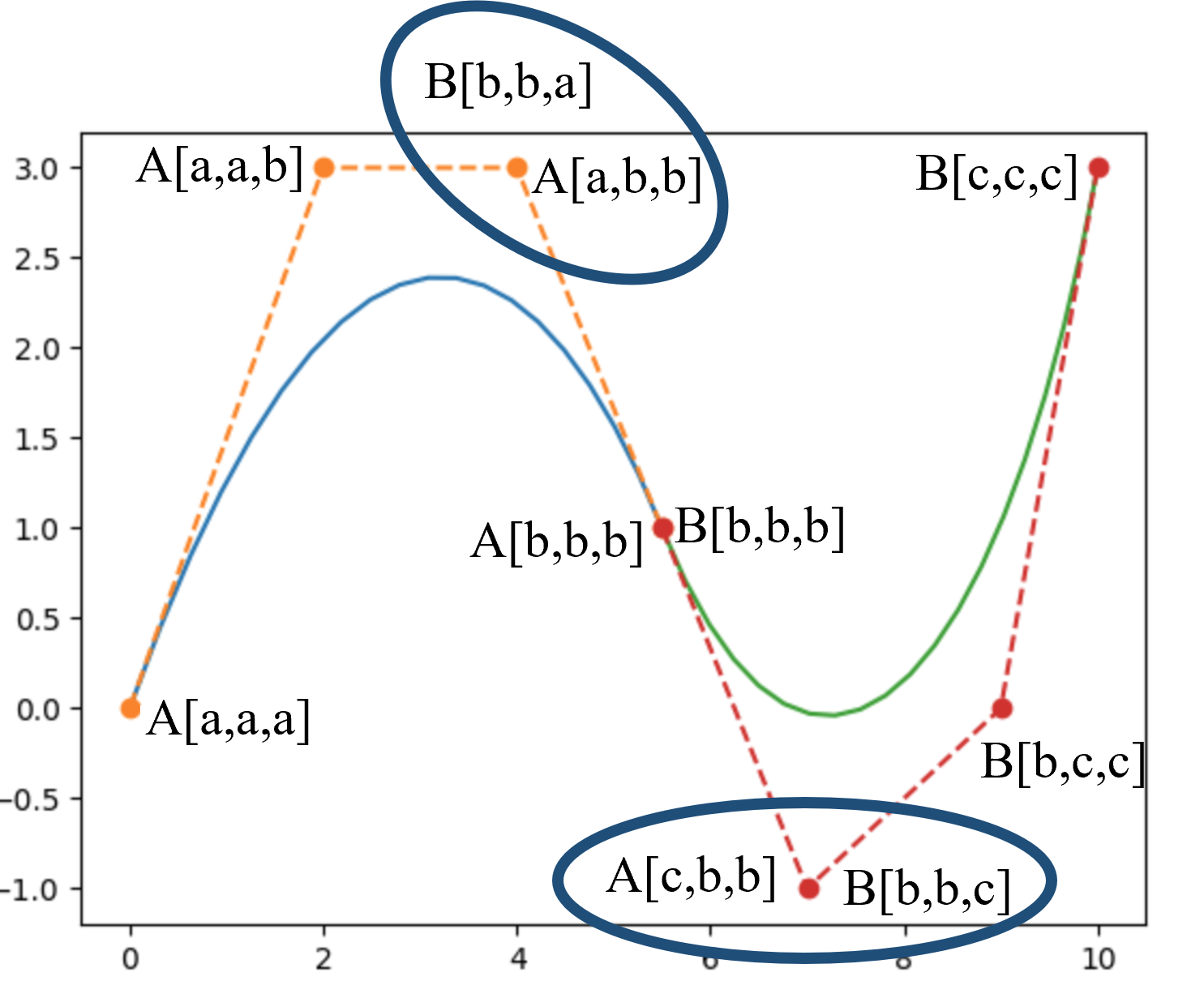
再进一步，如下图所示，达到$C^2$连续的条件为： $$ A[a,b,c]=B[a,b,c]\space\space\space(3) $$

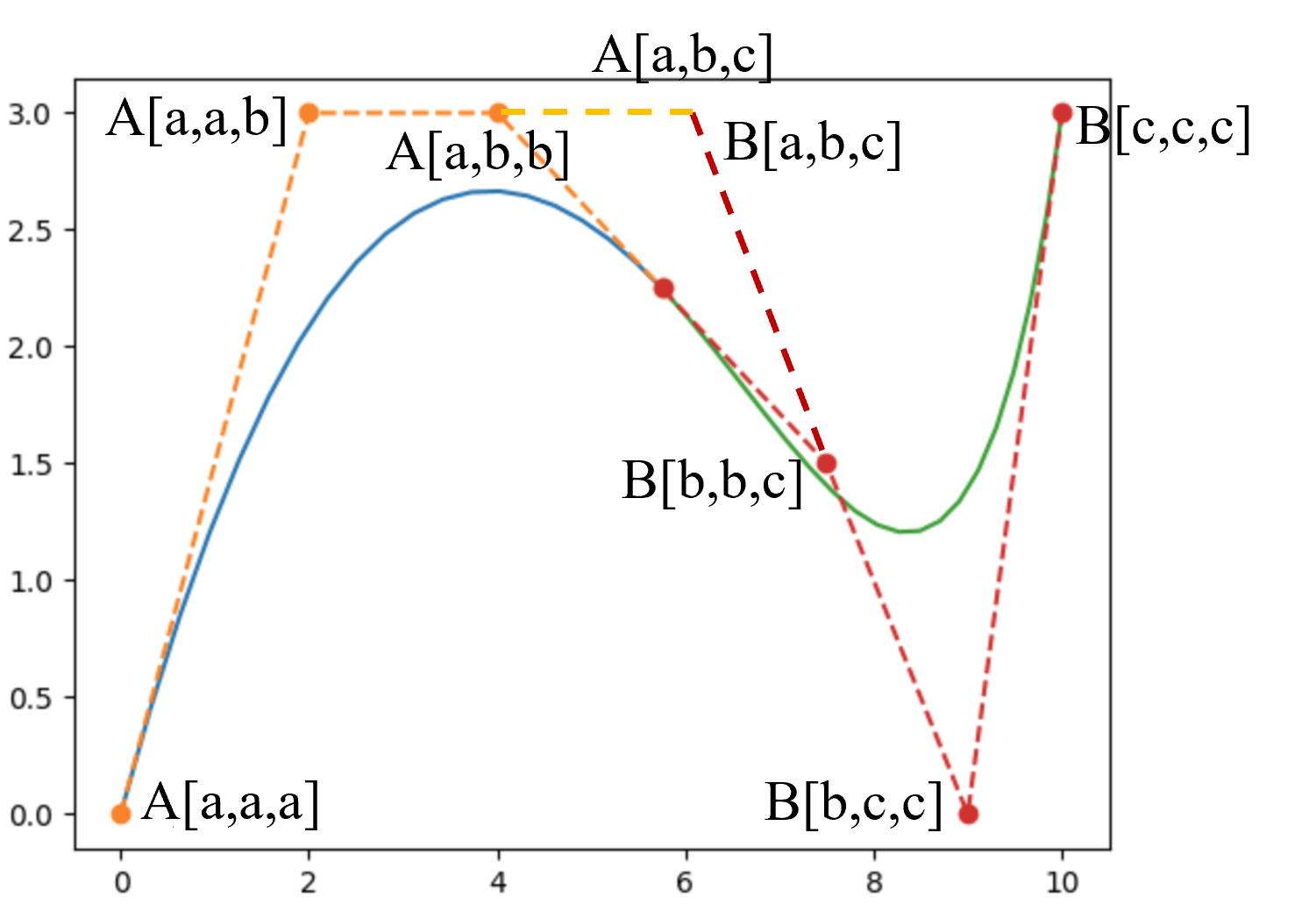
至此，上方B-spline的5个控制点的极坐标为： $$ \begin{array}{l} BS[a,a,a]\\BS[a,a,b]\\BS[a,b,c]\\ BS[b,c,c]\\BS[c,c,c] \end{array}\space\space\space(4) $$

则对应的极坐标下的knot vector为：$V=\left \{a,a,a,b,c,c,c\right \}$。

那么，对于由N条k阶的Bezier Curve组成的k阶B-spline，其控制点极坐标为： $$ \begin{array}{l} BS[u_0,u_0,...u_0](k个)\\ BS[u_0,u_0,...u_1]\\ ...\\ BS[u_N,u_N,...u_N](k个) \end{array}\space\space\space(5) $$

对应的knot vector是：

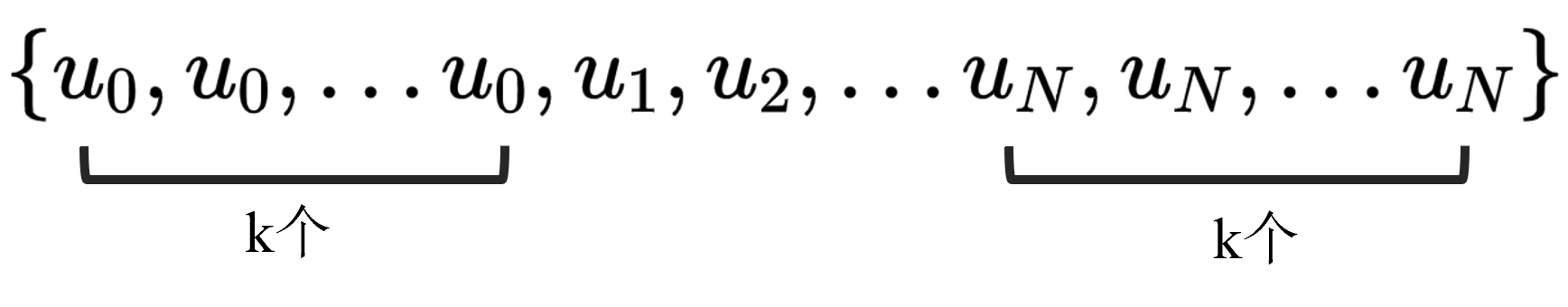
3.de Boor Algorithm

通过B-spline控制点找到对应的Bezier Curve的控制点，然后分段画Bezier Curve。以下图为例，一条由6个控制点控制的3阶B-spline。那么可知它是由3条3阶的Bezier Curve组成的。

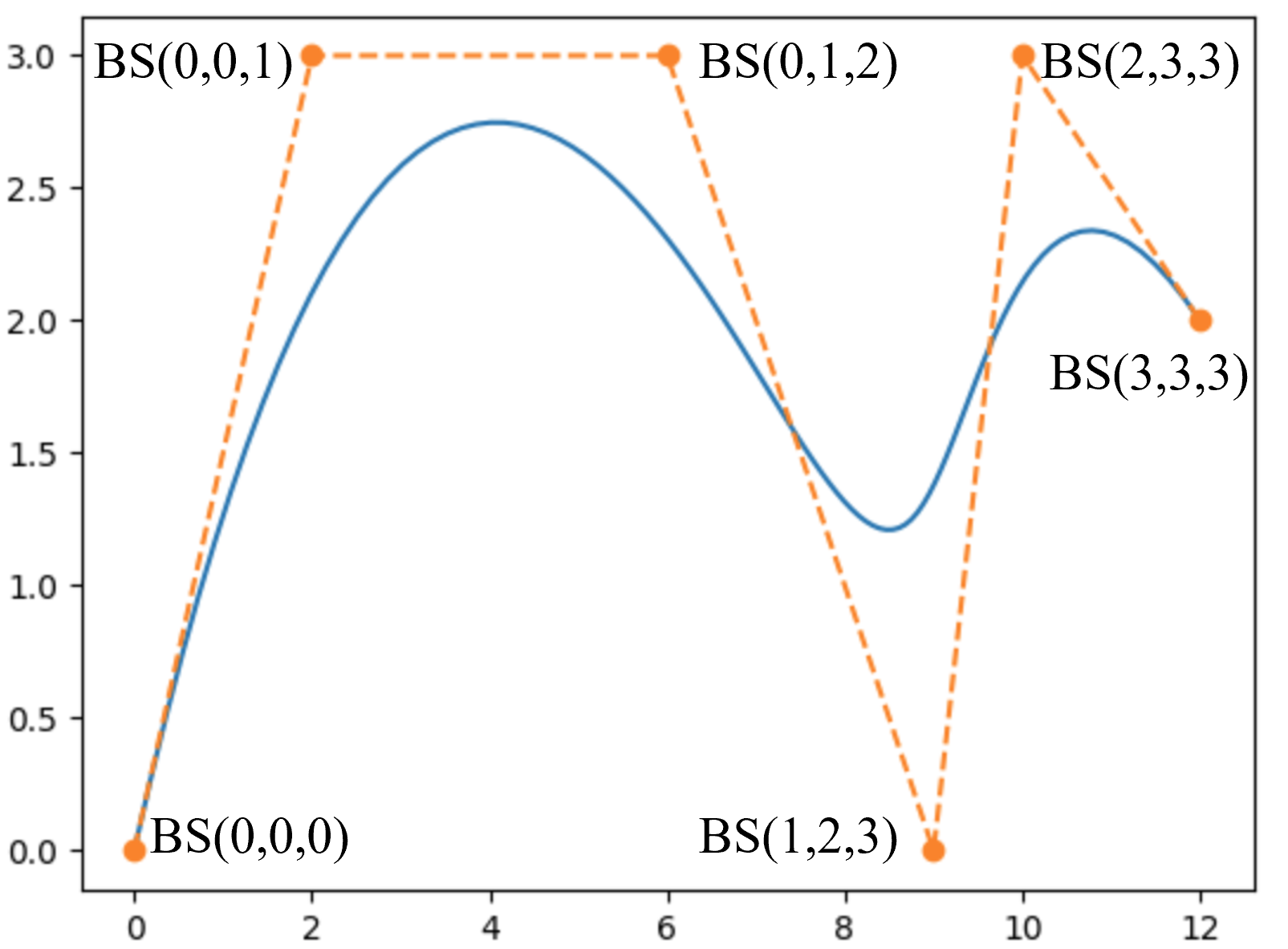
那么通过如下计算，就能获得3条Bezier Curve的控制点了。

$$ \begin{array}{l} BS(0,1,1)=\frac{BS(0,1,0)+BS(0,1,2)}{2}=\frac{BS(0,0,1)+BS(0,1,2)}{2}\\ BS(1,1,2)=\frac{2BS(0,1,2)+BS(3,1,2)}{3}=\frac{2BS(0,1,2)+BS(1,2,3)}{3}\\ BS(1,2,2)=\frac{BS(1,0,2)+2BS(1,3,2)}{3}=\frac{BS(0,1,2)+2BS(1,2,3)}{3}\\ BS(2,2,3)=\frac{BS(1,2,3)+BS(3,2,3)}{2}=\frac{BS(1,2,3)+BS(2,3,3)}{2}\\ BS(1,1,1)=\frac{BS(0,1,1)+BS(2,1,1)}{2}=\frac{BS(0,1,1)+BS(1,1,2)}{2}\\ BS(2,2,2)=\frac{BS(1,2,2)+BS(3,2,2)}{2}=\frac{BS(1,2,2)+BS(2,2,3)}{2} \end{array}\space\space\space(6) $$

然后画出整条B-spline，如下图所示。

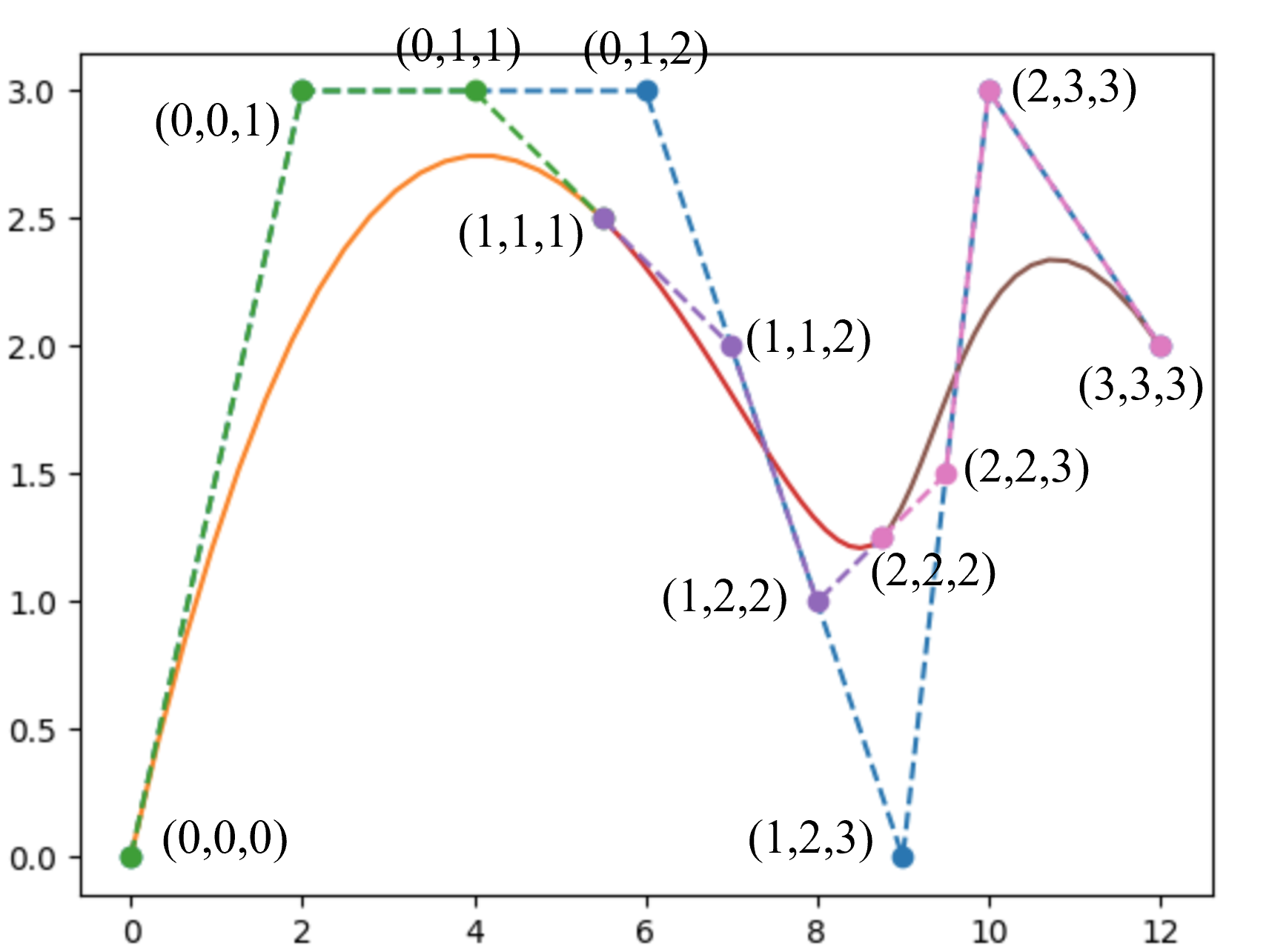
这种方法还可以通过极坐标找到B-spline上指定点。

 相关代码参见：https://github.com/Larissa1990/bezier_and_bspline_generator

Refs:

https://en.wikiversity.org/wiki/CAGD/B-splines#Polar_Form_of_B-spline_Points

https://pages.mtu.edu/~shene/COURSES/cs3621/NOTES/spline/B-spline/bspline-derv.html