Brief Introduction of Bezier Curve and Bspline: B-spline (1)

1.什么是B-spline

Bezier Curve的缺点主要是：

• nonlocality，移动一个控制点会影响整条曲线
• 高阶曲线，曲线离控制点很远

对此，可以把N条Bezier Curve组合起来。如下图所示，是两条3次Bezier Curve在D点连接而得。

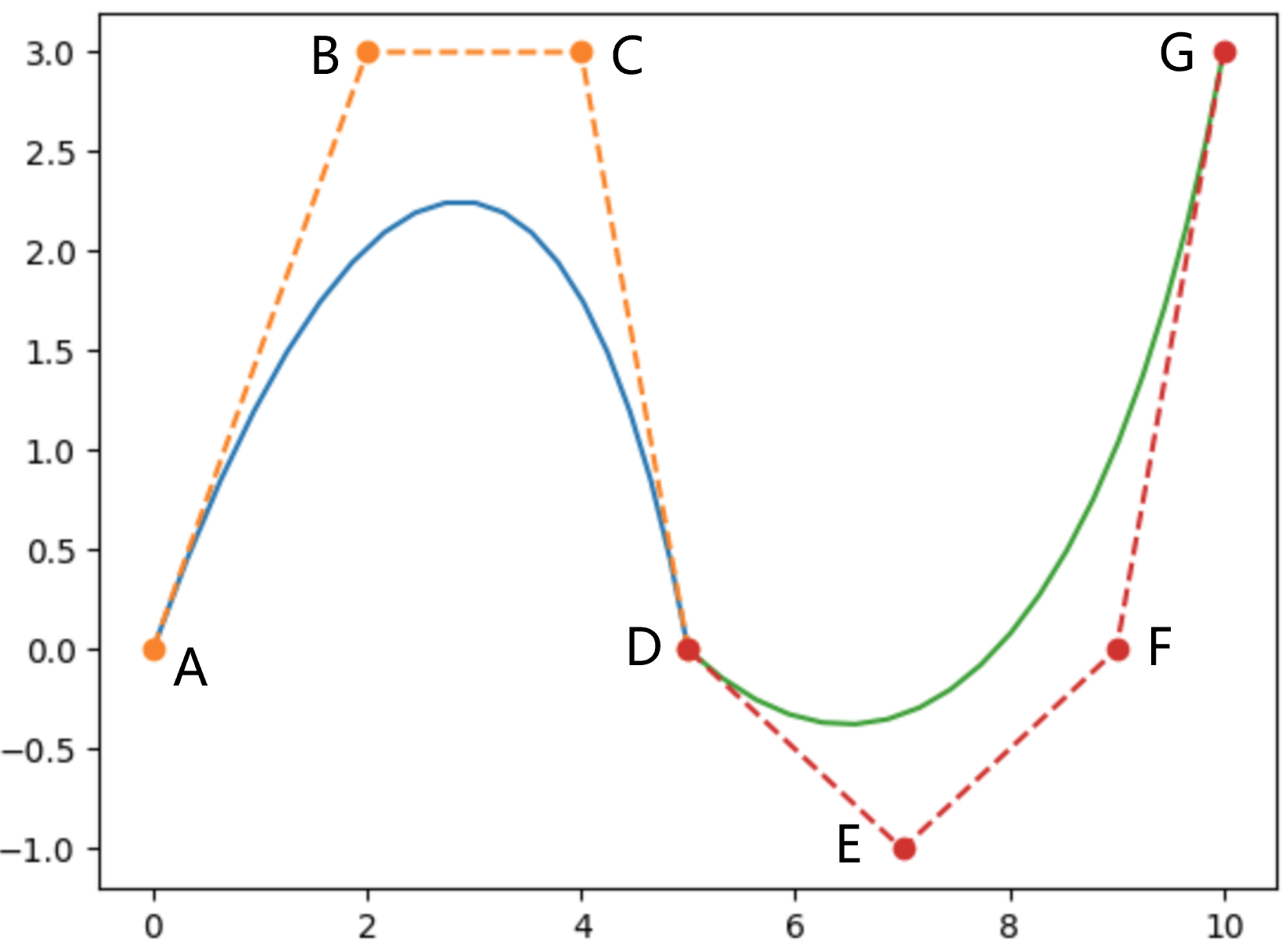
此时，该曲线是一条$C^0$曲线，共有7个控制点。若想得到一条$C^1$曲线，则需要两条Bezier Curve在D点的导数相同。通过Bezier Curve的导数表达式，可知需要C,D,E点共线并且$|CD|=|DE|$。此时D点失去了控制作用，共用6个控制点，如下图所示。

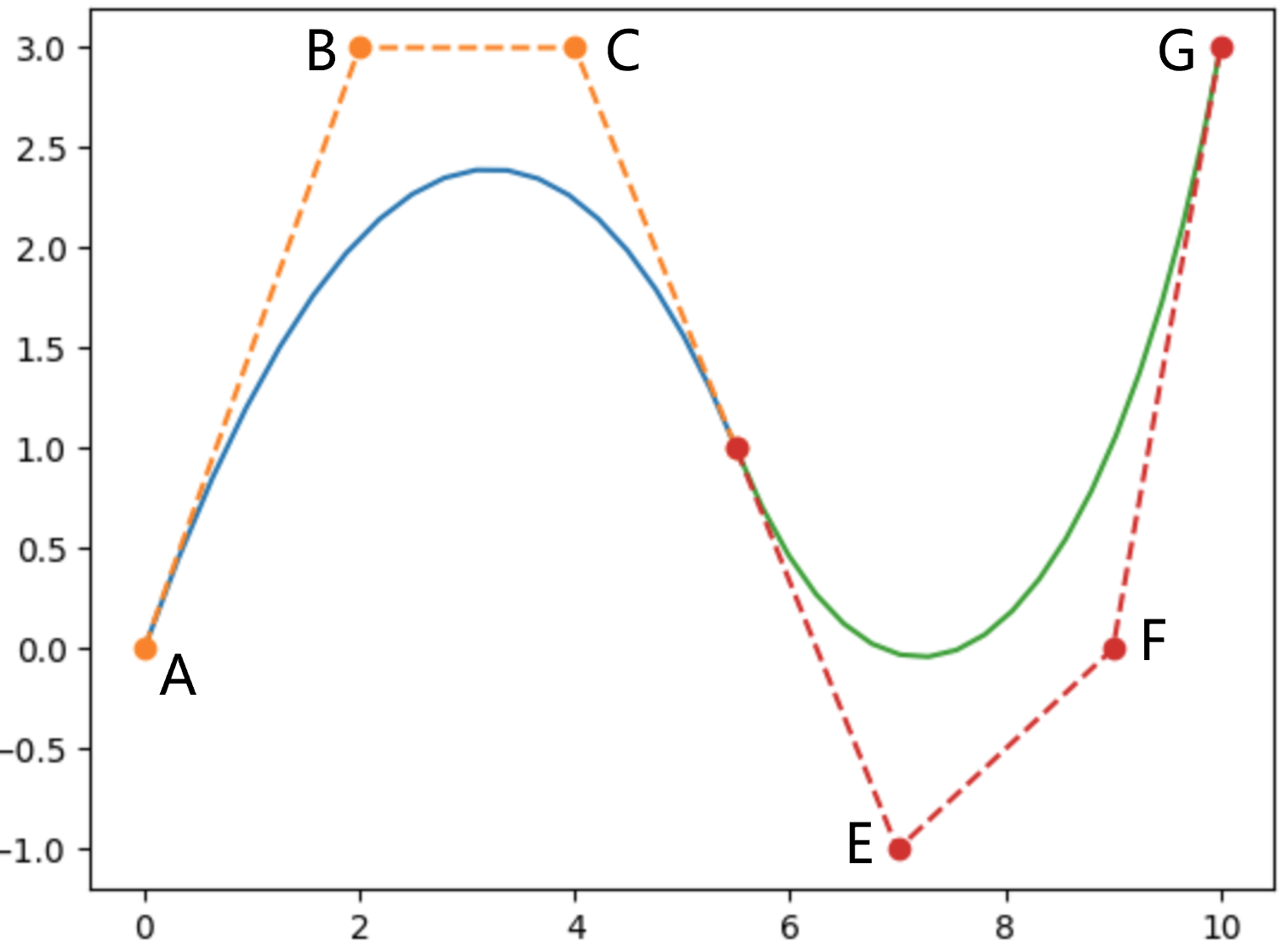
进一步地，若想得到一条$C^2$曲线，则需要D点的二阶导数相同。那么此时需要又一个控制点失去作用，例如E点，如下图所示。

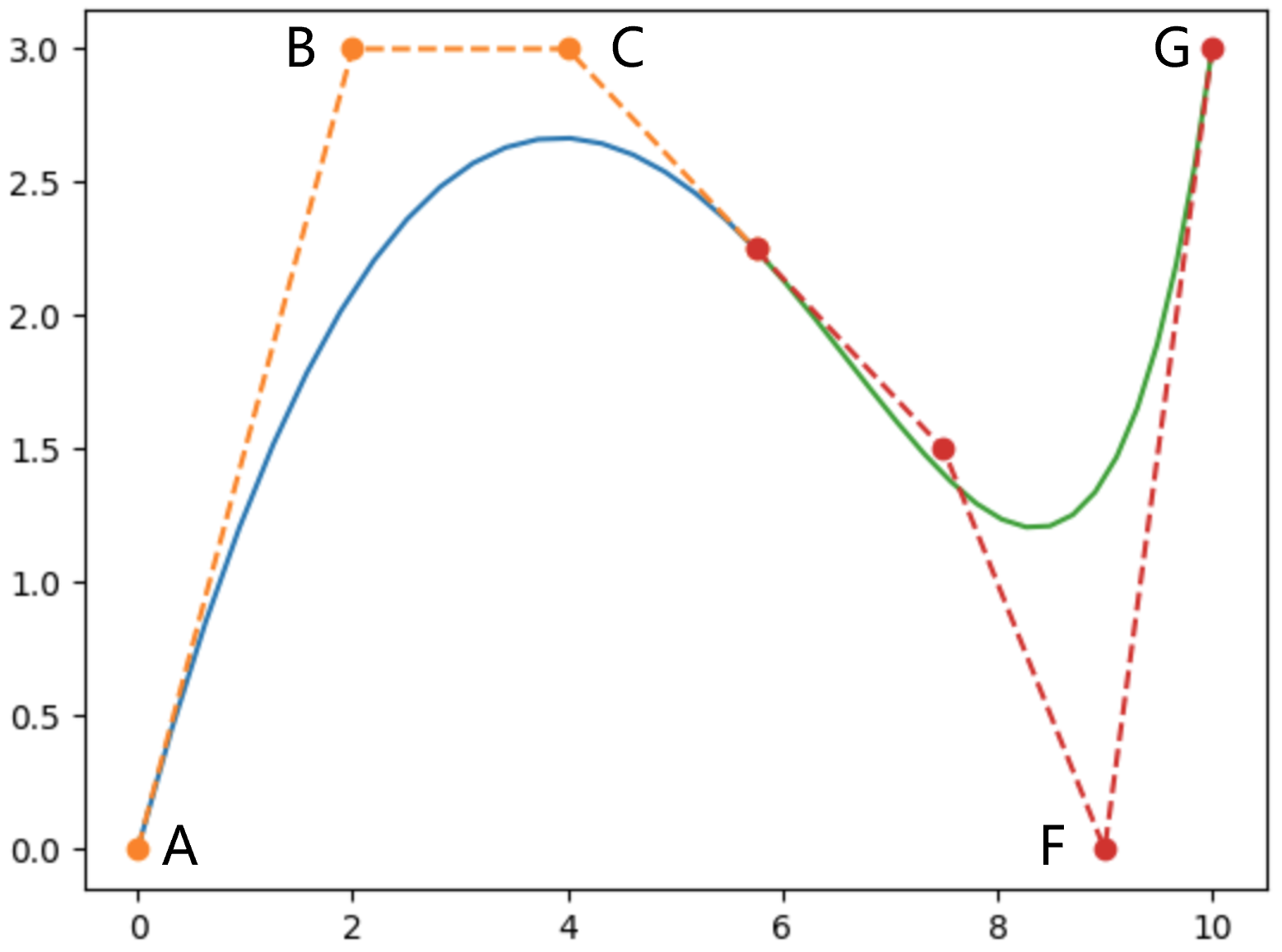
可见，N条3阶Bezier Curve拼接成一条$C^0$曲线，需要$4N-(N-1)=3N+1$个控制点；一条$C^1$曲线需要$3N+1-(N-1)=2N+2$个控制点；一条$C^2$曲线需要$2N+2-(N-1)=N+3$个控制点。

进而，N条k阶的Bezier Curve拼接成一条$C^{k-1}$连续的B-spline曲线需要N+k个控制点。

但值得注意的是，在上图中，A,B,C,F,G并不是B-spline的控制点，控制点应该是下图的S0-S4。

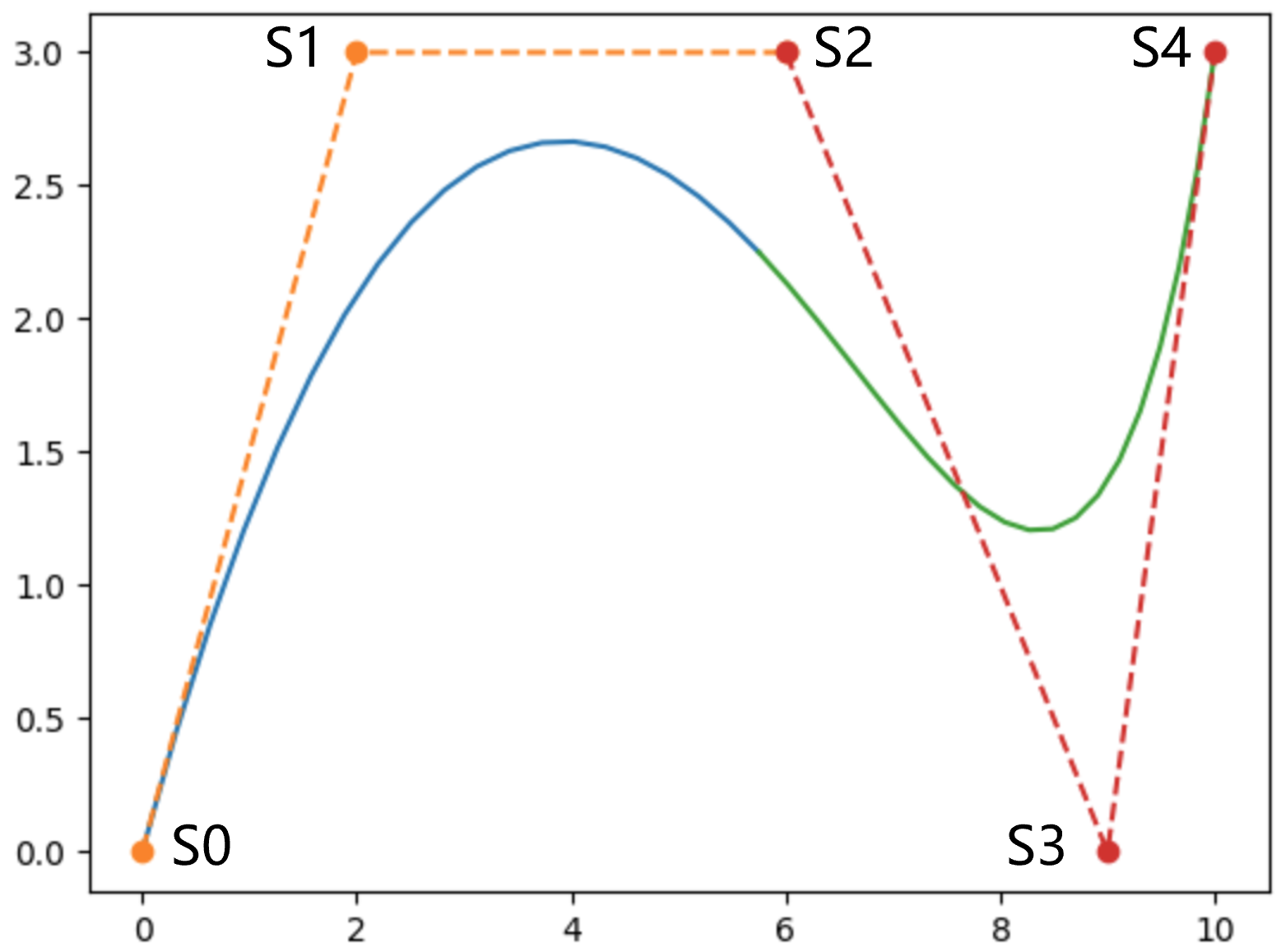
B-spline具有局部性，例如移动S0，并不会对第二段Bezier Curve产生影响。同样地，移动S4，也不会对第一段Bezier Curve产生影响。B-spline的性质可总结为：

• The curve starts and ends at the first and last control vertices. 
• The curve is tangent to the first and last edges of its control polygon. 
• The B-spline curve is contained in the convex hull of its control polygon. 如下图所示。
• If the B-spline curve is of degree n, it is contained in the union of the convex hulls of every n+1 consecutive vertices. 如下图所示。

 

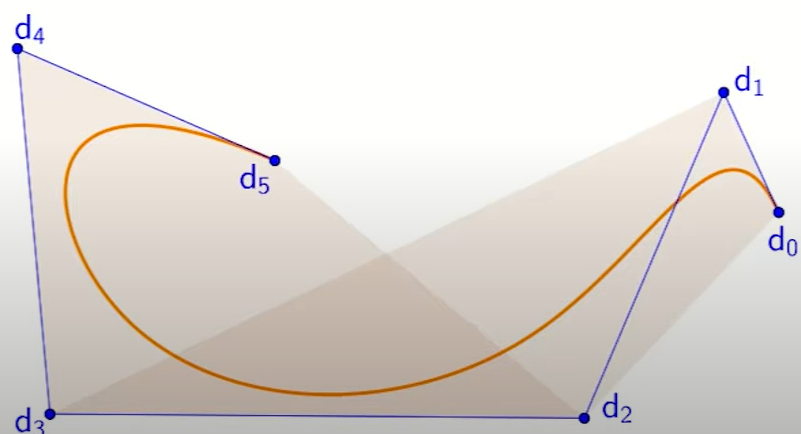
• The shape of the B-spline curve is roughly the same as the shape of its control polygon.
• The B-spline curve twists less than its control polygon. 如下图所示。

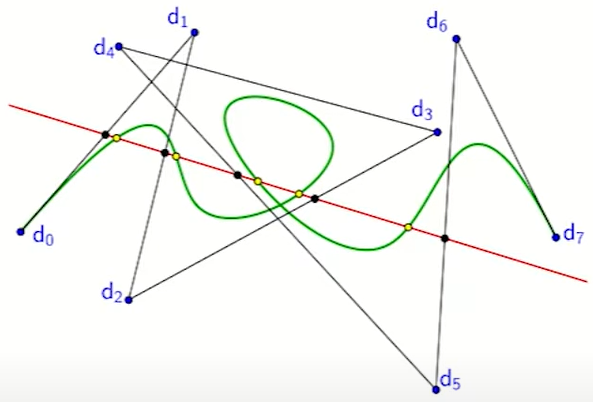
• Moving a vertex of the control polygon affects only a part of the curve close to the vertex moved.
• The B-spline curve can be translated, rotated or reflected, by translating, rotating, or reflecting the vertices of its control polygon.

2.B-spline表达式

由N条k阶的Bezier Curve组成k阶B-spline曲线有N+k个控制点。B-spline的表达式可以写为：

$$BS(t)=\sum_{i=0}^{N+k-1}P_iB_{i,k}(t)\space\space\space t\in[0,N]\space\space\space (1)$$

当N=3,k=3时，对应的6个基函数如下图所示。

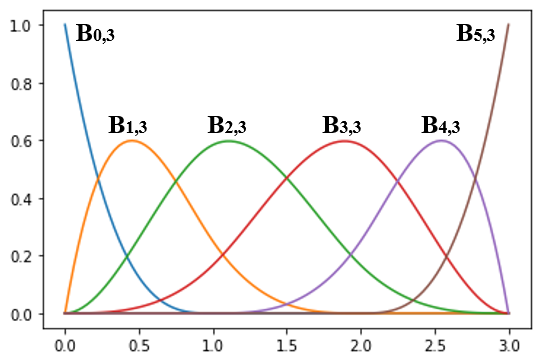
可见，基函数$B_{0,3}$的有效区间，即值不为零的区间是[0,1]，基函数$B_{1,3}$的有效区间是[0,2]。

The knots of a B-spline curve are the endpoints of the supports of the basis functions that define the curve. 这6个基函数的knots为： $$\begin{array}{l} supp B_{0,3}=[0,1]\\ supp B_{1,3}=[0,2] \\ supp B_{2,3}=[0,3]\\ supp B_{3,3}=[0,3]\\ supp B_{4,3}=[1,3]\\ supp B_{5,3}=[2,3] \end{array}$$

The knot vector comprises the knots of the basis functions that define a S-spline curve, listed from smallest to largest. 上方B-spline对应的knot vector为$V=\left \{0,0,0,0,1,2,3,3,3,3\right \}$。

N条k阶Bezier Curve组成的k阶B-spline曲线对应的knot vector为：

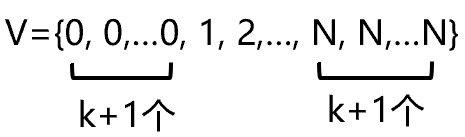
3.Cox-de boor formula

要想根据控制点生成B-spline，需要计算出相应的基函数。本小节就是一种用knot vector递归计算出基函数的算法。以上方的3阶B-spline为例，他的思想就是通过$B_{0,0}$和$B_{1,0}$得到$B_{0,1}$，以及通过$B_{1,0}$和$B_{2,0}$得到$B_{1,1}$，进而通过$B_{0,1}$和$B_{1,1}$得到$B_{0,2}$，如此递归地得到$B_{0,3}-B_{5,3}$。

计算公式如下： $$B_{i,k}(t)=\frac{t-V[i]}{V[i+k]-V[i]}B_{i,k-1}(t)+\frac{V[i+k+1]-t}{V[i+k+1]-V[i+1]}B_{i+1,k-1}(t)\space\space\space(2)$$ 并且 $$B_{i,0}(t)=\begin{cases} 1,\space\space\space t\in[V[i],V[i+1]) \\ 0,\space\space\space otherwise \end{cases}\space\space\space(3)$$ 以及$B_{i,0}=0\space\space if\space V[i]=V[i+1]$，以及分母为0，则为0。

python代码详见：https://github.com/LiuLarissa/bezier_and_bspline_generator/blob/master/bspline_generator.py

4.B-spline的微分

针对B-spline如下的表达式： $$BS(t)=\sum_{i=0}^NB_{i,k}(t)P_i\space\space\space(4)$$ 基函数的一阶导数为： $$\frac{dB_{i,k}(t)}{dt}=B'_{i,k}(t)=\frac{k}{t_{i+k}-t_i}B_{i,k-1}(t)-\frac{k}{t_{i+k+1}-t_{i+1}}B_{i+1,k-1}(t)\space\space\space(5)$$ 则B-spline的一阶导数为： $$BS'(t)=\frac{k}{t_k-t_0}B_{0,k-1}(t)P_0+k\sum_{i=0}^{n-1}B_{i+1,k-1}(t)\frac{P_{i+1}-P_i}{t_{i+k+1}-t_{i+1}}-\frac{k}{t_{n+k+1}-t_{n+1}}B_{n+1,k-1}(t)P_n\space\space\space(6)$$ 式(6)中的第一项和最后一项为0，则 $$BS'(t)=\sum_{i=0}^{N-1}B_{i+1,k-1}(t)Q_i\space\space\space(7)$$ 其中： $$Q_i=\frac{k}{t_{i+k+1}-t_{i+1}}(P_{i+1}-P_i)\space\space\space(8)$$ 可见，一条k阶的B-spline的导数是另一条k-1阶的B-spline，控制点则变为了$Q_0,Q_1,...Q_{n-1}$，少了一个。针对这条k-1阶的B-spline，其knot vector就是之前的knot vector去掉第一个和最后一个元素。那么针对新的knot vector，B-spline的微分可以写为： $$BS'(t)=\sum_{i=0}^{N-1}B_{i,k-1}(t)Q_i\space\space\space(9)$$