Brief Introduction of Bezier Curve and Bspline: Bezier Curve
1.什么是Bezier Curve
下文通过例子说明什么是Bezier Curve。如下图所示,给定4个控制点,A=(0,0), B=(2,3), C=(4,3), D=(5,0)。

点E,F,G分别为线段AB,线段BC和线段CD上的动点,满足:
$$ t_1=\frac{AE}{AB}=\frac{BF}{BC}=\frac{CG}{CD}\space\space\space (1) $$
go on,点H,I分别为线段EF和线段FG上的动点,点J为线段HI上的动点,满足:
$$ t_2=\frac{EH}{EF}=\frac{FI}{FG}\space\space\space (2) $$
$$ t_3=\frac{HJ}{HI}\space\space\space (3) $$
令$t_1=t_2=t_3=t,\space\space\space t\in[0,1]$,如下图所示。

动点J的轨迹就是根据A,B,C,D四个控制点生成的cubic bezier curve。如下方动图所示。

以上面的例子为例,推导Bezier Curve的表达式。首先,很容易能得到下面这些表达式。
$$ \begin{array}{l} E=(1-t_1)A+t_1B\\ F=(1-t_1)B+t_1C\\ G=(1-t_1)C+t_1D\\ H=(1-t_2)E+t_2F\\ I=(1-t_2)F+t_2G\\ J=(1-t_3)H+t_3I \end{array} $$
令$t_1=t_2=t_3=t$,处理下可得: $$ J(t)=(1-t)^3A+3t(1-t)^2B+3t^2(1-t)C+t^3D\space\space\space t\in[0,1]\space\space\space (4) $$
并且系数和为1,即
$$ (1-t)^3+3t(1-t)^2+3t^2(1-t)+t^3=1\space\space\space (5) $$
推广下可得,n个控制点(P0,P1,...Pn-1)控制下的Bezier Curve表达式为: $$ Bezier(n,t)=\sum_{i=0}^{n-1}C_{n-1}^it^i(1-t)^{n-1-i}P_i\space\space\space t\in[0,1]\space\space\space(6) $$
可见,n个控制点的Bezier Curve的表达式是一个n-1阶的多项式。这个阶数也是Bezier Curve的阶数,或称为次数(本文交替使用阶和次)。
2.Bezier Curve极坐标表达
一条3阶的Bezier曲线用极坐标方式可表达为:$Bezier=F(t,t,t) \space\space\space t\in [0,1]$
四个控制点A,B,C,D分别表示为:$F(0,0,0),\space F(1,0,0),\space F(1,1,0),\space F(1,1,1)$
点E,F,G,H,I分别表示为:$F(t,0,0),F(t,1,0),F(t,1,1),F(t,t,0),F(t,t,1)$
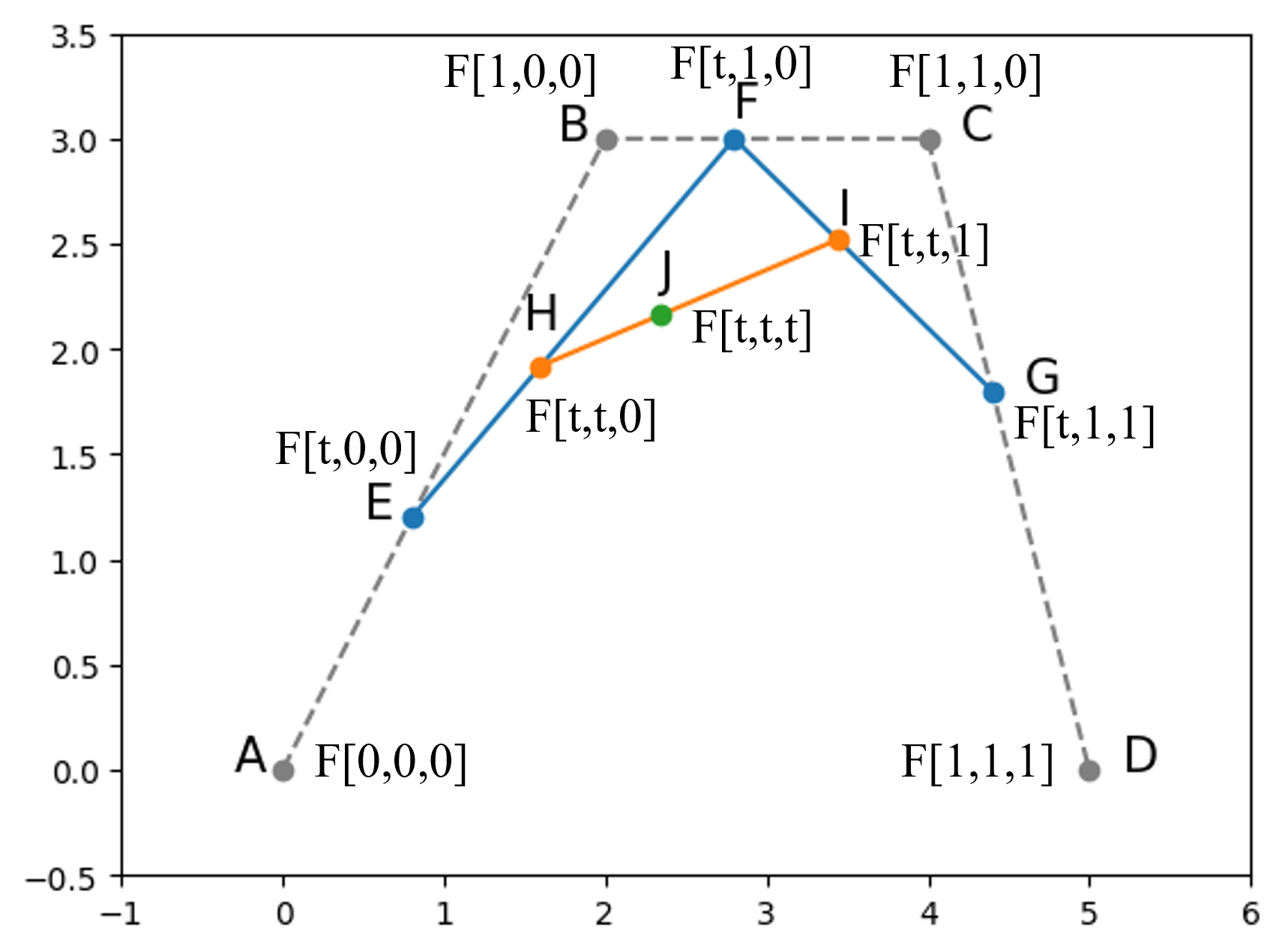
极坐标形式具有对称性。例如$F(t,0,0)=F(0,0,t)=F(0,t,0)$。
3.Bezier Curve导数
对式(6)求一阶导数,可得: $$ B'(n,t)=(n-1)\sum_{i=0}^{n-2}C_{n-2}^it^i(1-t)^{n-2-i}(P_{i+1}-P_i)\space\space\space(7) $$
可见,这也是一条Bezier曲线,但阶数降低了一阶,并且控制点改变了。
4.Bezier Curve性质
在教科书中,给定n+1个控制点的n次Bezier曲线表达式写为: $$p(t)=\sum_{i=0}^nP_iB_{i,n}(t)\space\space\space t\in[0,1] $$
其中,$P_i$是控制点,$B_{i,n}(t)$称为Bernstein基函数。
n=3时,共有4个控制点,对应的4个基函数如下图所示。
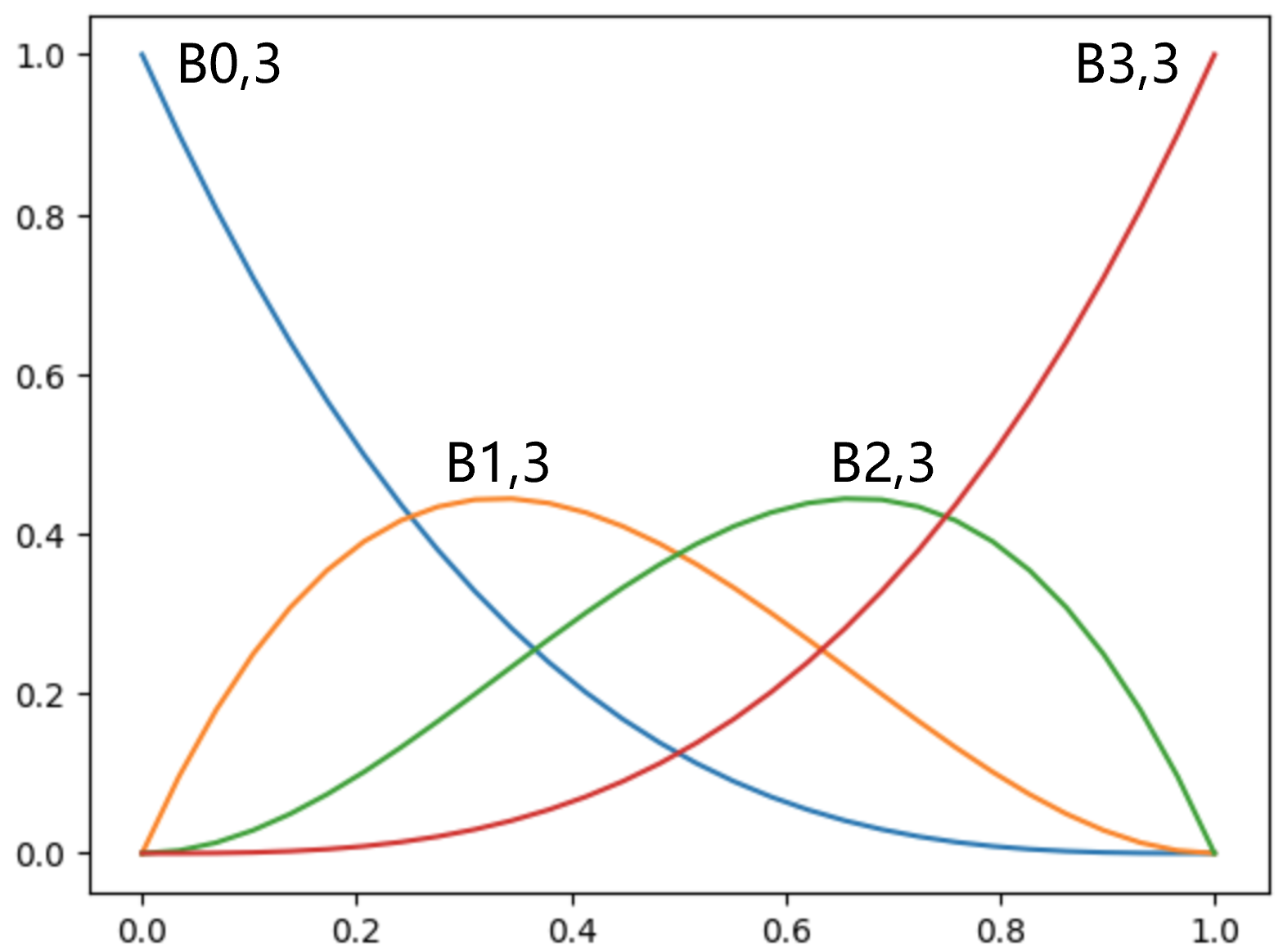
Bezier Curve的性质:
- 端点性质,Bezier曲线的首末端点分别是控制点的起始点和终止点。
- 端点切矢,Bezier曲线在首末端点的r阶导数只与(r+1)个相邻控制点有关,与其余控制点无关。
- 对称性,保持n阶Bezier曲线的控制点位置不变,把次序反转,构造出的新Bezier曲线与原曲线形状相同,走向相反,镜像关系。
- 凸包性质,Bezier曲线位于控制多边形构成的凸包之内,而且永远不会超出凸包的范围。
- 几何不变性,曲线只与控制点的位置有关,与坐标系的选择无关。
- 仿射不变性,对Bezier曲线所作的任意仿射变换,相当于先对控制点做变换,再根据变换后的控制点构造新曲线。
- 变差缩减性,如果控制多边形是一个平面图形,则平面内的任意直线与Bezier曲线的交点个数不多于该直线与控制多边形的交点个数。这意味着如果控制多边形没有摆动,那么曲线也不会摆动,就是说Bezier曲线比控制多边形的折线更加光滑。
5.Rational Bezier Curve 有理Bezier曲线
$$p(t)=\frac{\sum_{i=0}^n\omega_iP_iB_{i,n}(t)}{\sum_{i=0}^n\omega_iB_{i,n}(t)} \space\space\space t\in[0,1] $$
其中,$\omega_i$是控制点的权。如果所有权因子等于1,根据Bernstein基函数的权性,方程中分母等于1,转化为非有理n次Bezier曲线。规定所有权因子都为非负值,有理Bezier曲线保留了上方所述的非有理Bezier曲线的所有性质。
Refs
1.https://wiki.freecad.org/B-Splines
2.https://www.youtube.com/watch?v=xkMToaSF_78&list=PL8bSwVy8_IcMvtI70tZoYesCS0hGVO5qd
3.计算机图形学(微课版)



