数据结构之二叉树(Binary Tree)_python实现

1.二叉树的类定义

2.二叉树的基本性质

3.遍历二叉树

      3.1前序遍历

      3.2中序遍历

      3.3后序遍历

      3.4层次遍历

4.二叉树的应用

      4.1二叉搜索树

      4.2平衡二叉树

      4.3红黑树

      4.4线段树

      4.5堆

5.参考文献

1.二叉树的类定义

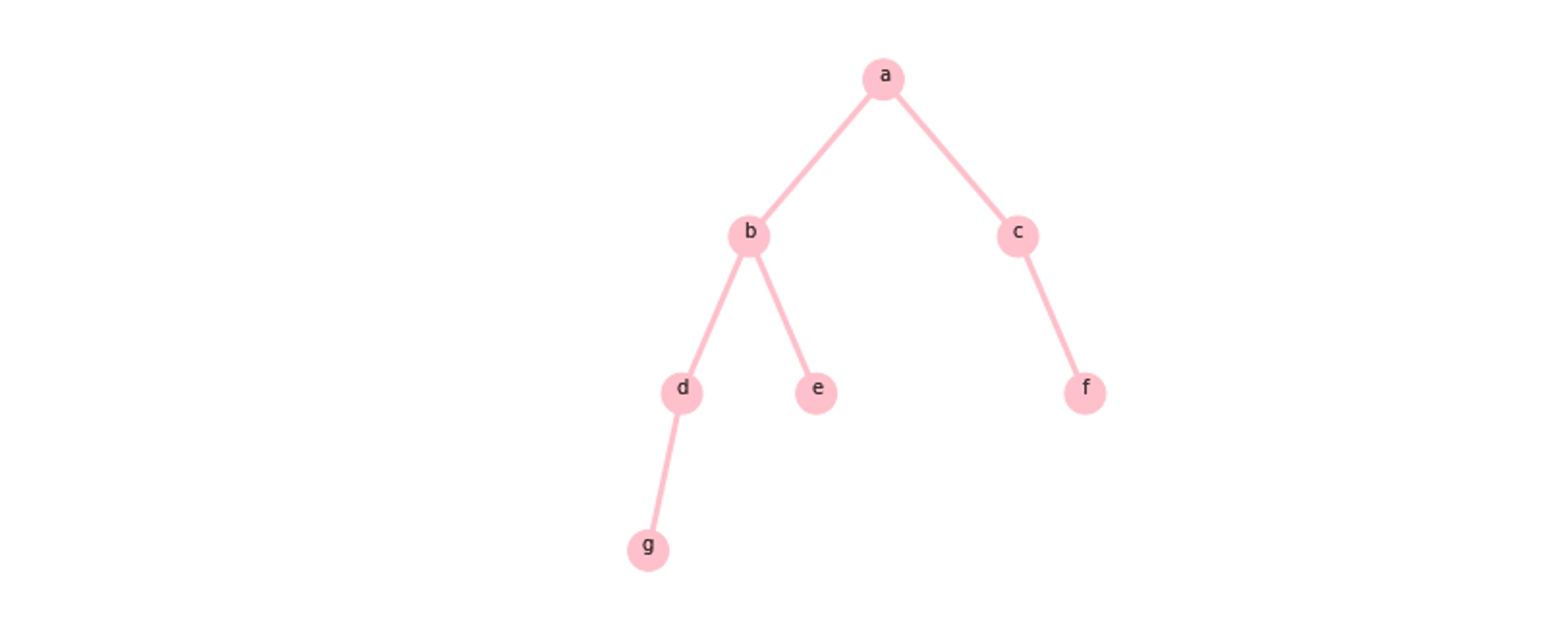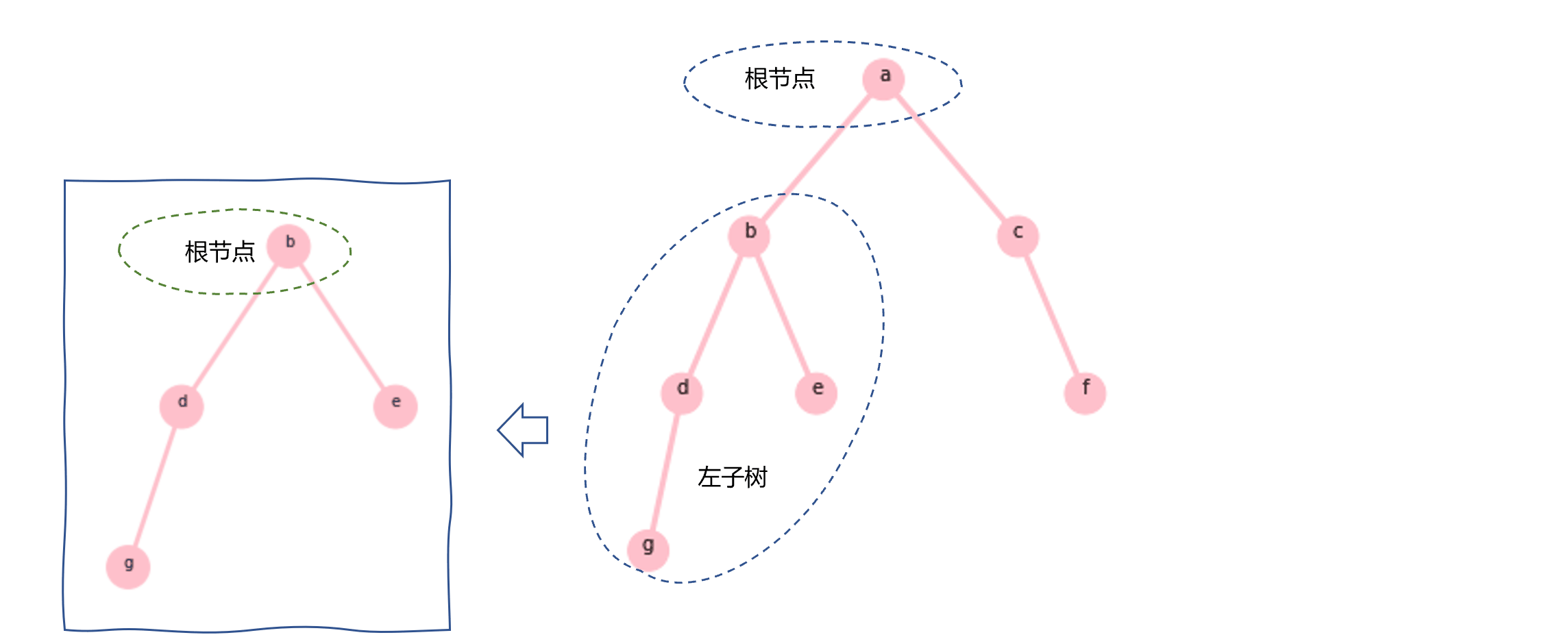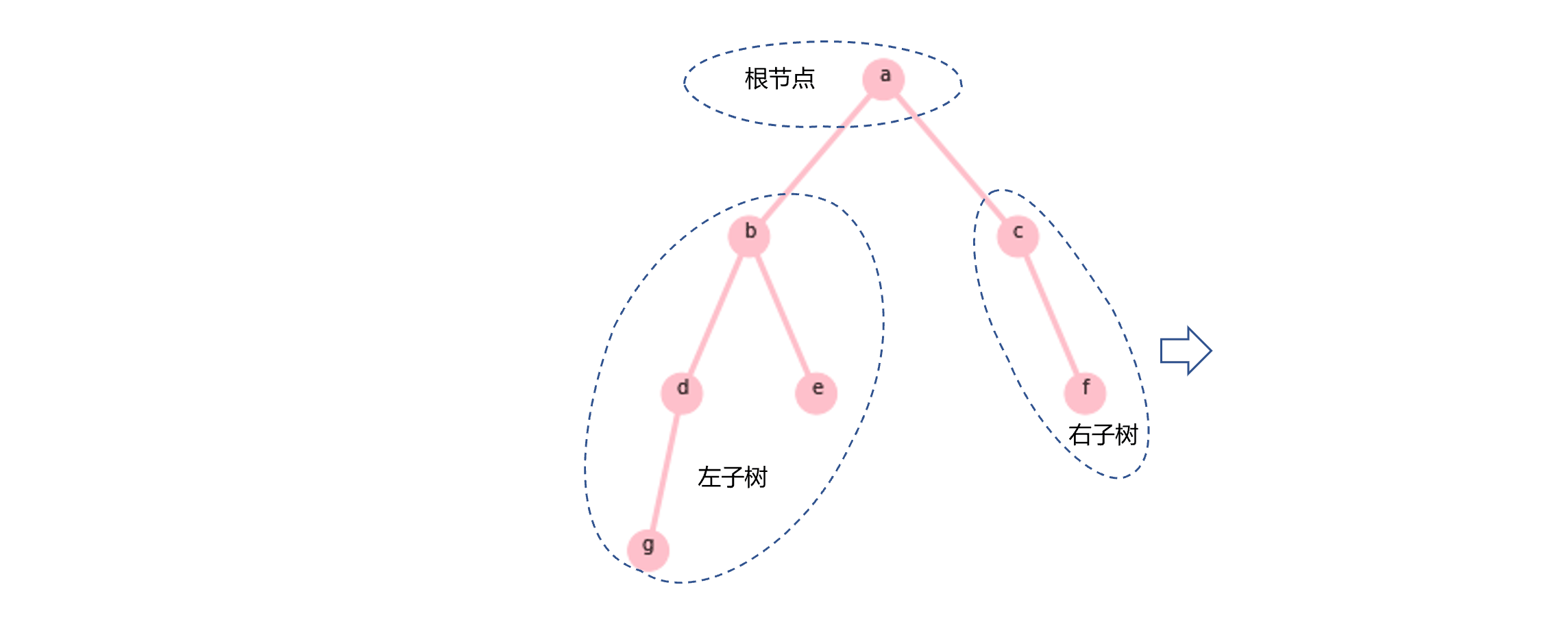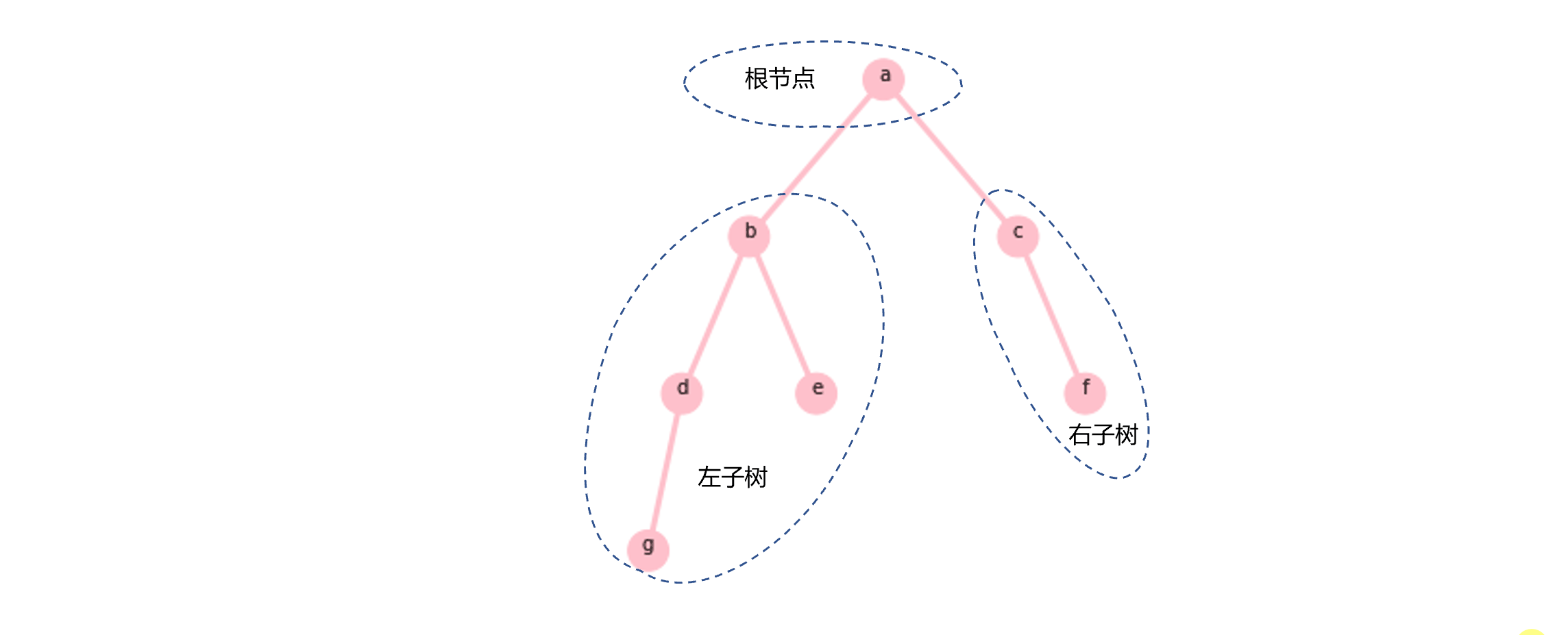
如图1.1所示，二叉树就是一个节点只有一个值，并且最多有两个子树的一种树结构。也就是说，二叉树中的一个节点可以有0、1、2个子树，有0个子树的节点称为叶子节点。子树也是二叉树。

 

图1.1 二叉树的结构

图1.1所示的是一棵根节点为a的二叉树，它有两个子树。其中左子树是一棵根节点为b的二叉树，右子树是一棵根节点为c的二叉树。通常，二叉树的类定义如下所示：

# python
class TreeNode:
    def __init__(self,val=None,left=None,right=None):
        self.val=val
        self.left=left
        self.right=right
BinaryTree in Python
// C#
public class TreeNode
{
    public object val;
    public TreeNode left;
    public TreeNode right;
    
    public TreeNode(object val){
        this.val=val
    }
}
BinaryTree in C#

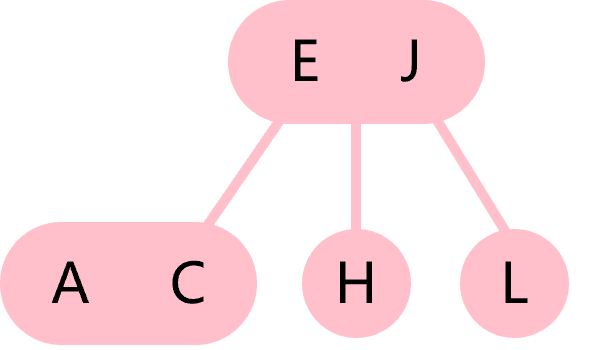
节点只有一个值的意思就是图1.2所示的这棵树就不属于二叉树，而是一棵2-3树。它的根节点包含E和J两个值，在本文中将这样的节点称为3节点，而二叉树的节点称为2节点。可见3节点最多有三棵子树。

 

图1.2 2-3树

2.二叉树的基本性质

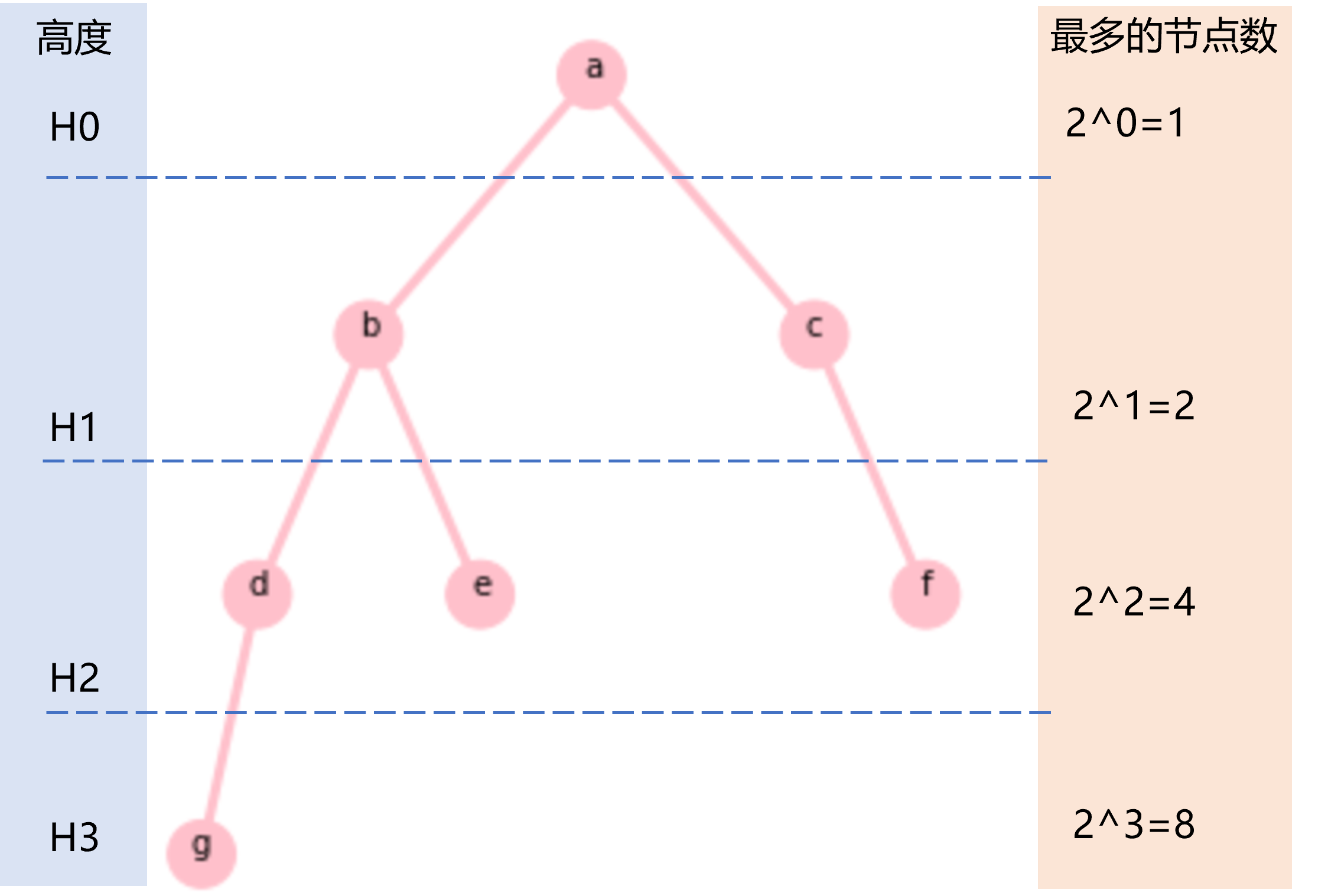
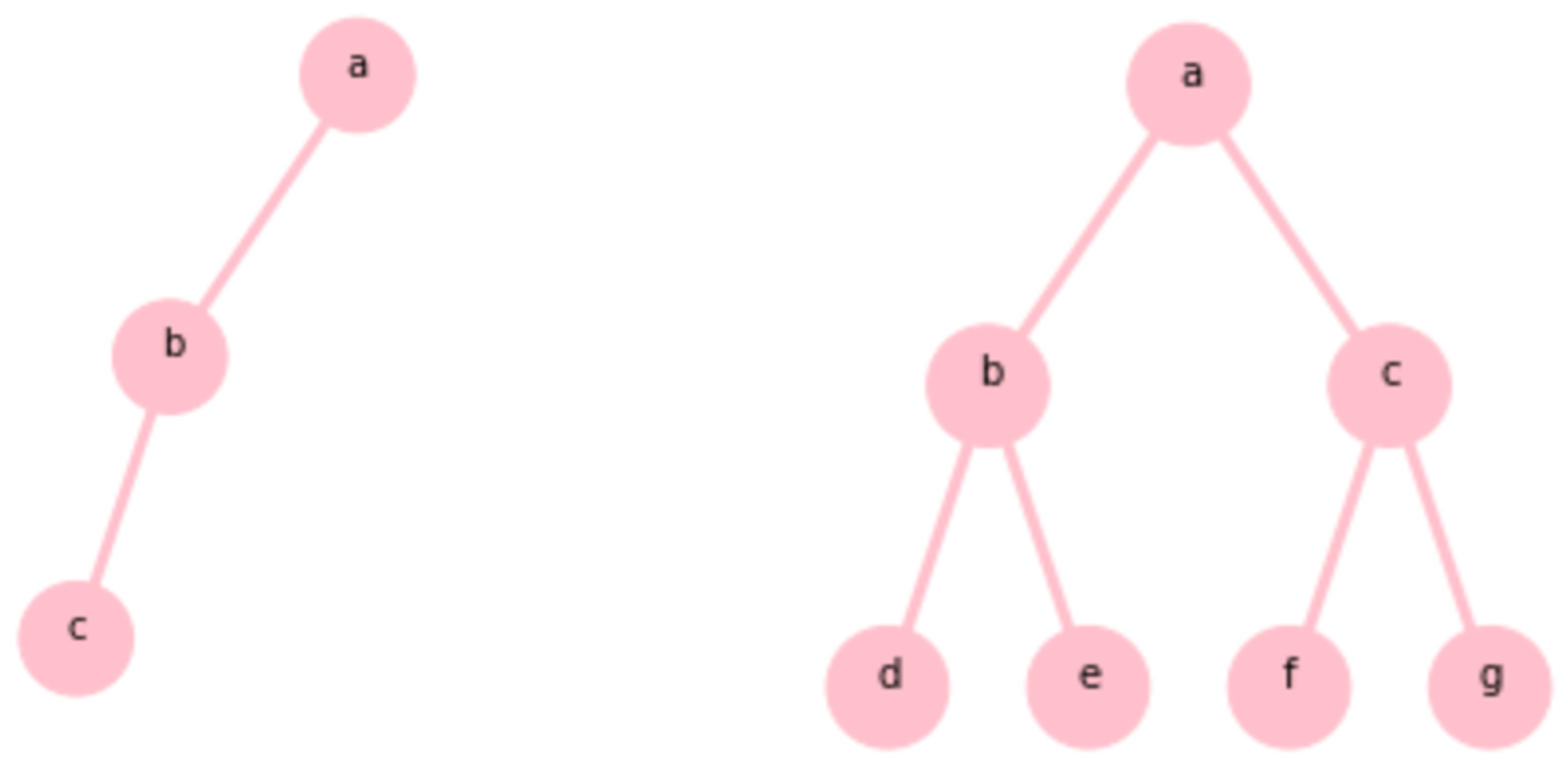
二叉树的高度就是从根节点到最深的叶子节点的路径上所经历果的节点数，例如图2.1所示的二叉树的高度为4。二叉树的第i层中的节点数最少为1个，最多为2i个，那么可知高度为h的二叉树的节点数的总和最少为h个，最多为20+21+……+2h-1=2h-1个。例如图2.2所示的两棵高度为3的二叉树，左树的总结点数为3，右树的总结点数为7。

图2.1 二叉树的高度和节点数

图2.2 高度为3的二叉树

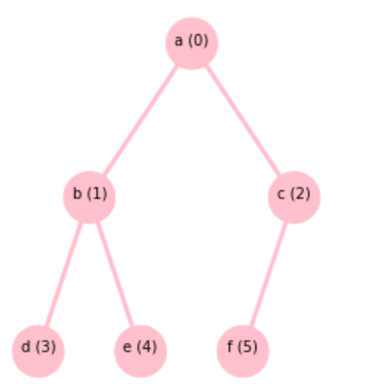
如果一棵二叉树除了最后一层外，每一层的节点数都是满的，且最后一层的节点全部集中在左侧，这样的树称为完全二叉树，如图2.3所示。

图2.3 完全二叉树

如果给节点编号，如图2.3所示。可见，索引为i的父节点的两个子树的根节点的索引为2*i+1和2*i+2；子树的根节点索引为i，那么其父节点是(i-1)//2。图2.3所示的完全二叉树可以用一维数组表示，即[a,b,c,d,e,f]。a的索引为0，它的两个子节点的索引分别为1和2，即b,c。

3.遍历二叉树

遍历二叉树就是依次输出二叉树的节点，那么根据遍历的顺序可分为：前序遍历、中序遍历、后序遍历、层次遍历等。

3.1.前序遍历

前序遍历的顺序是根节点在最前面，即：根节点-左子树-右子树。图1.1所示的二叉树的前序遍历过程如图3.1所示。

 

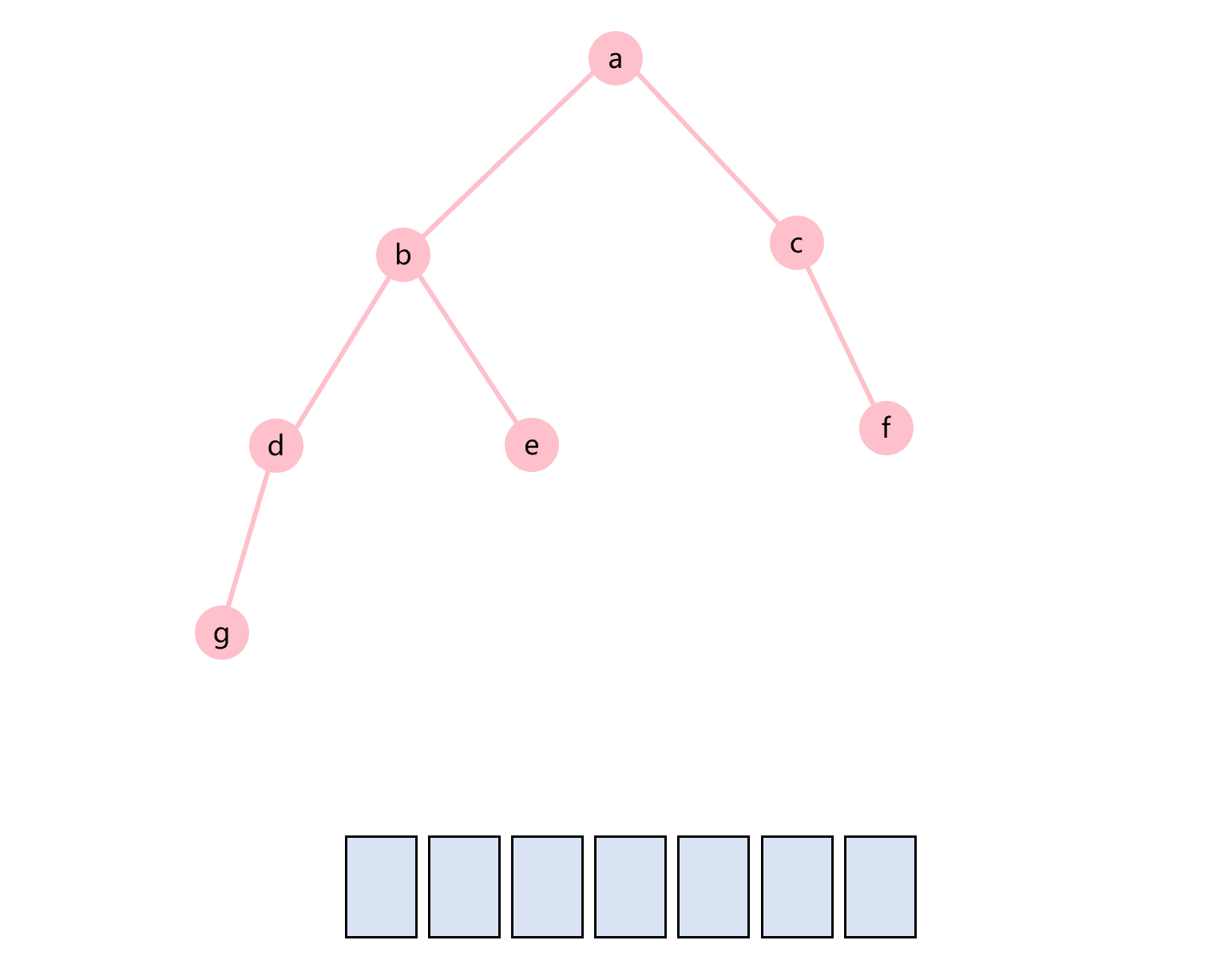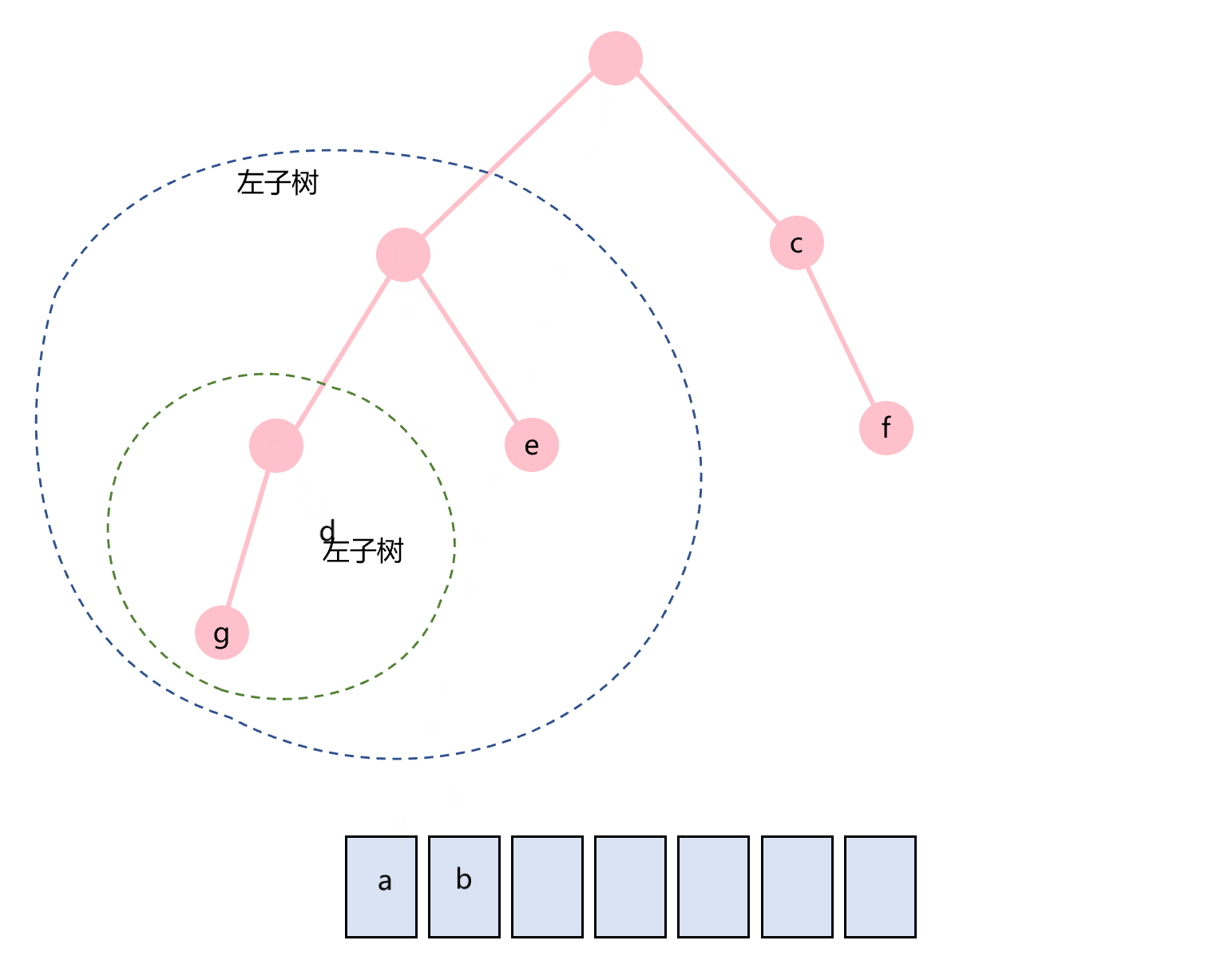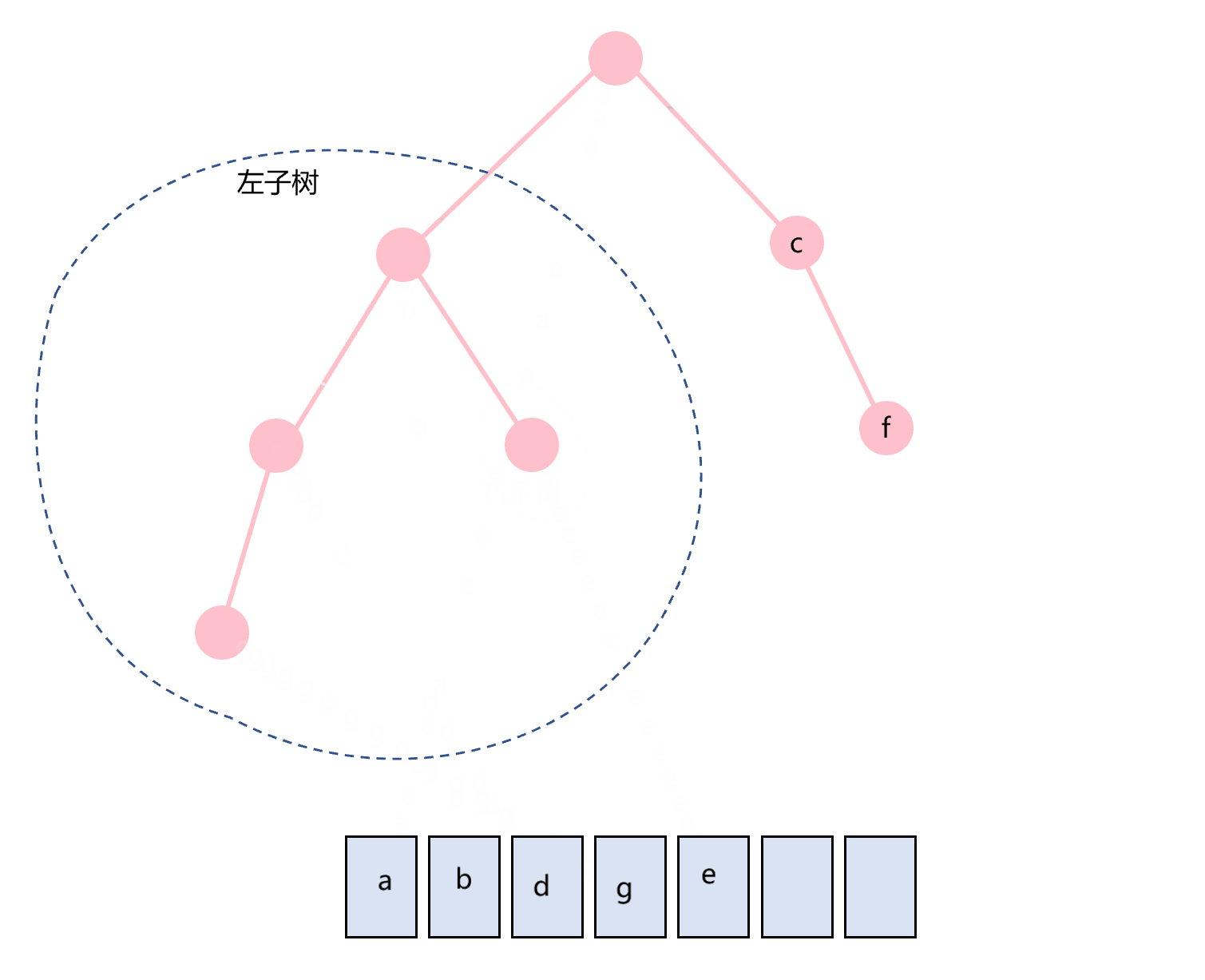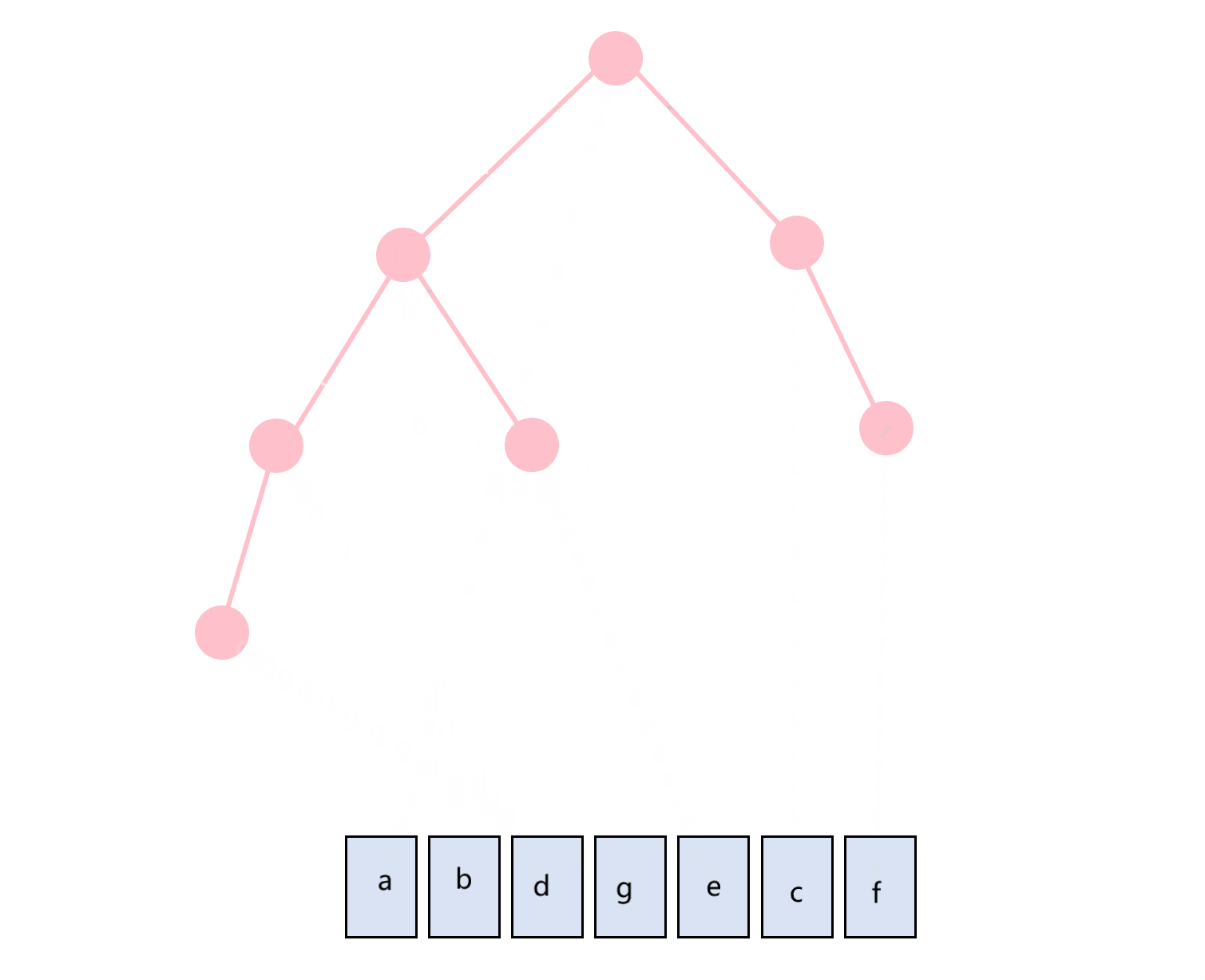
图3.1 前序遍历示意图

从上面的遍历过程来看，二叉树的遍历与递归算法完美契合。递归遍历左子树直到某个根节点的左子树是null为止，然后遍历其右子树，并不断地返回递归的上一层。代码如下：

nodes=[]
def preorderTraverse(node):
    if node:
        nodes.append(node.val)
        preorderTraverse(node.left)
        preorderTraverse(node.right)
preorder traverse

前序遍历还可以使用栈和while循环来实现，如图3.2所示。不断地将当前二叉树的右子树push到栈中，并将指针指向其左子树，当指向的左子树为null的时候，从栈中pop出一棵右子树二叉树，并重复这个过程。代码如下：

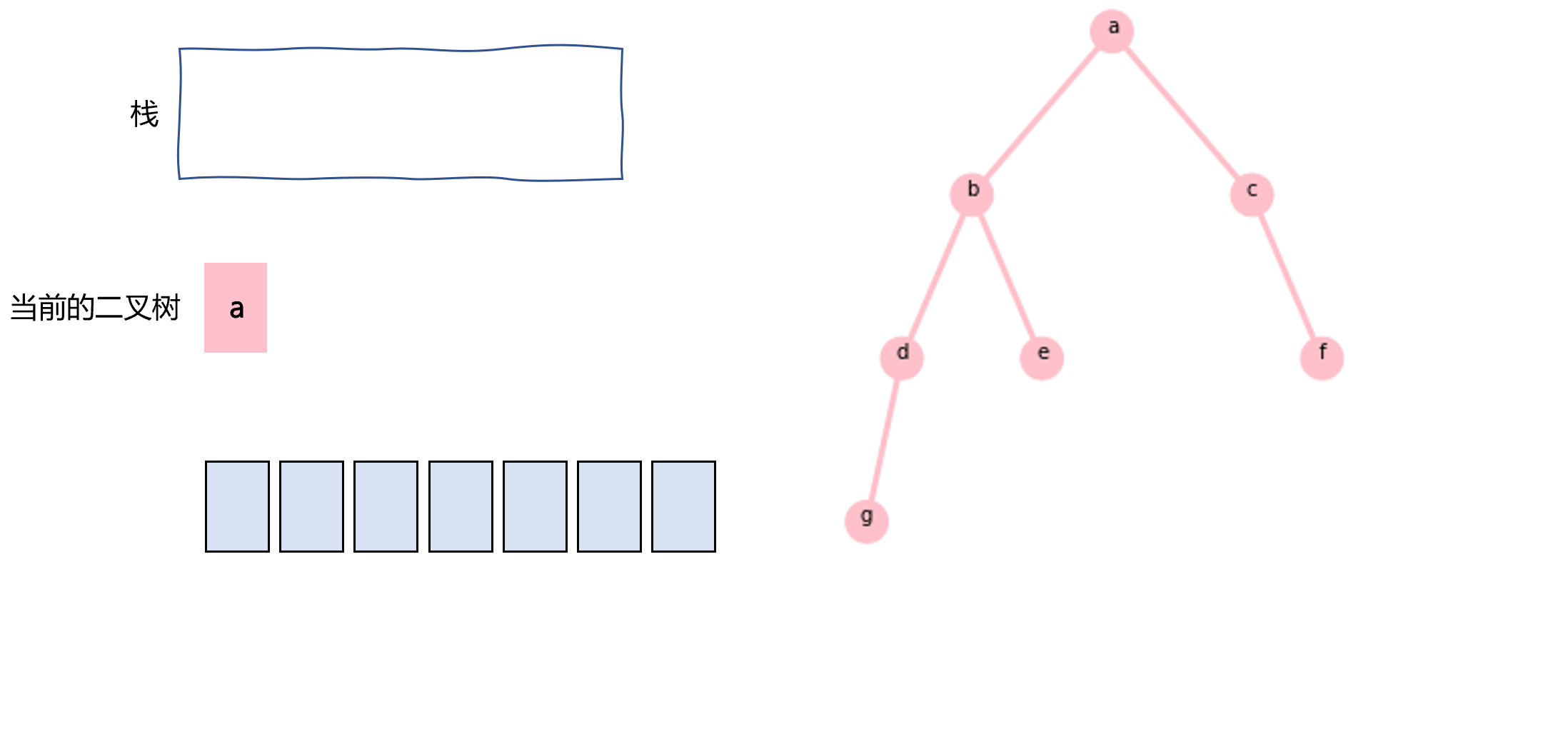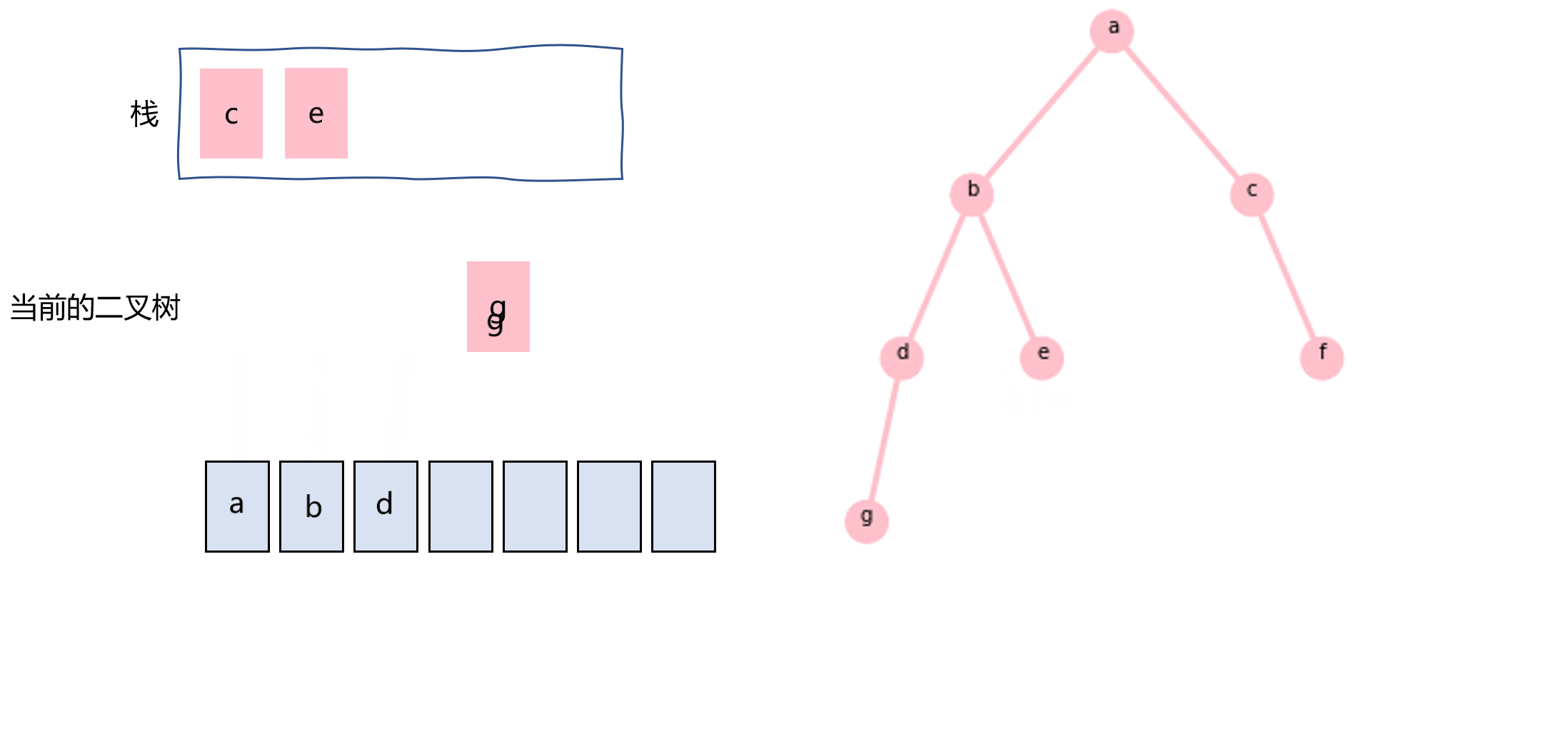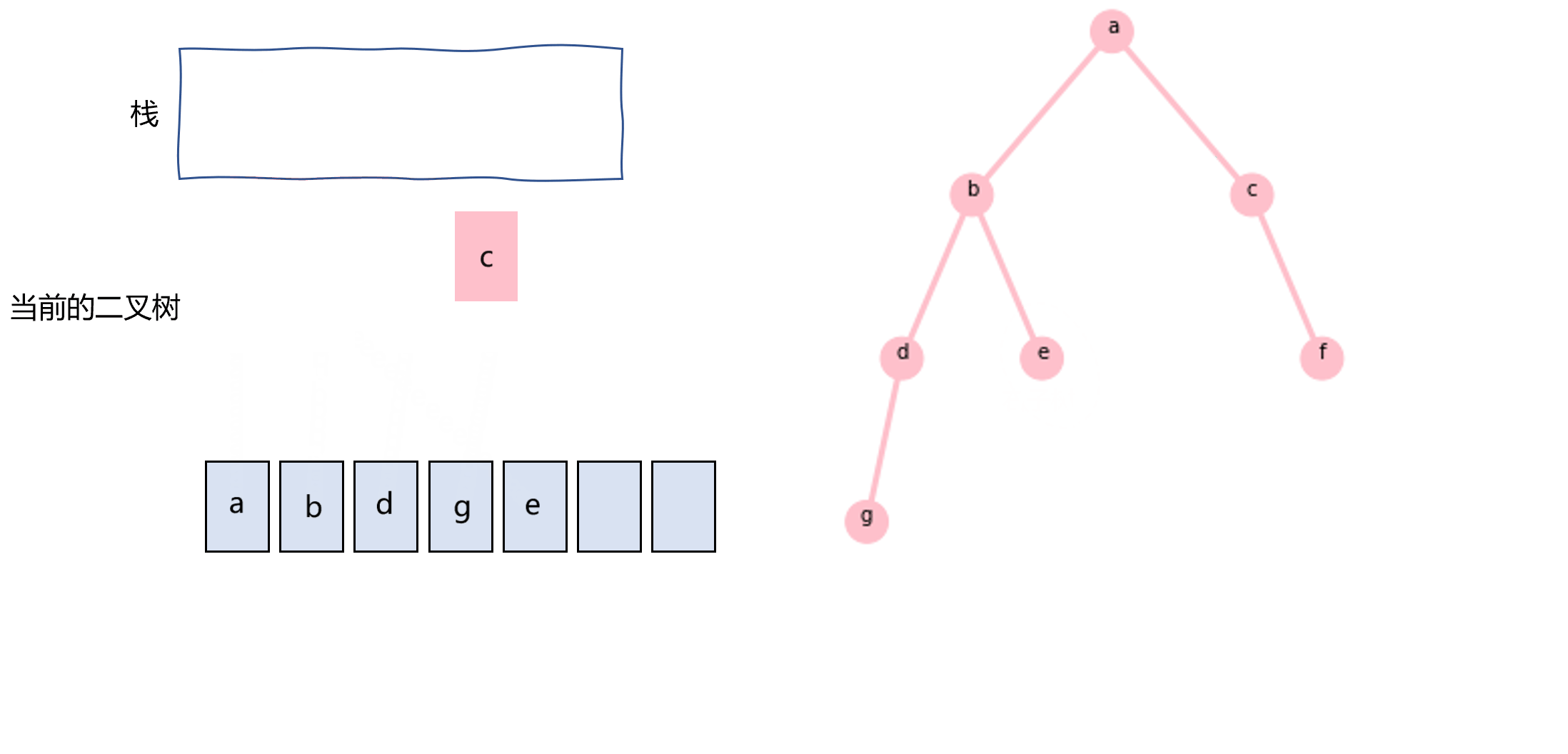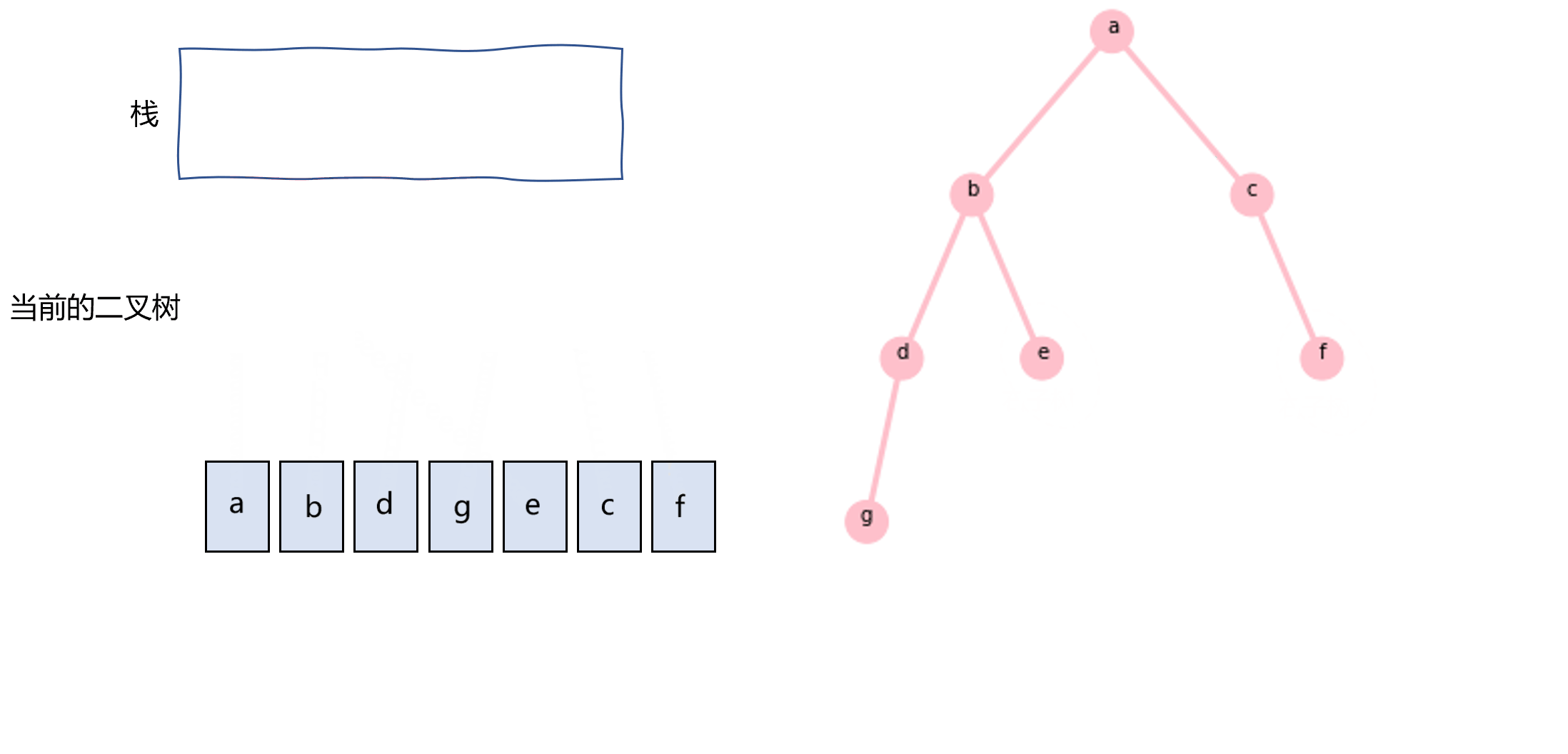
图3.2 使用栈实现前序遍历的过程示意图

nodes=[]
stack=[]
def preOrderTraverse(node):
    while node or len(stack)!=0:
        if node:
            if node.right:
                stack.append(node.right)
            nodes.append(node.val)
            node=node.left
        else:
            node=stack.pop()
preorder traverse

3.2.中序遍历

中序遍历的顺序是根节点在中间，即：左子树-根节点-右子树。图1所示的二叉树的中序遍历过程如图3.3所示。

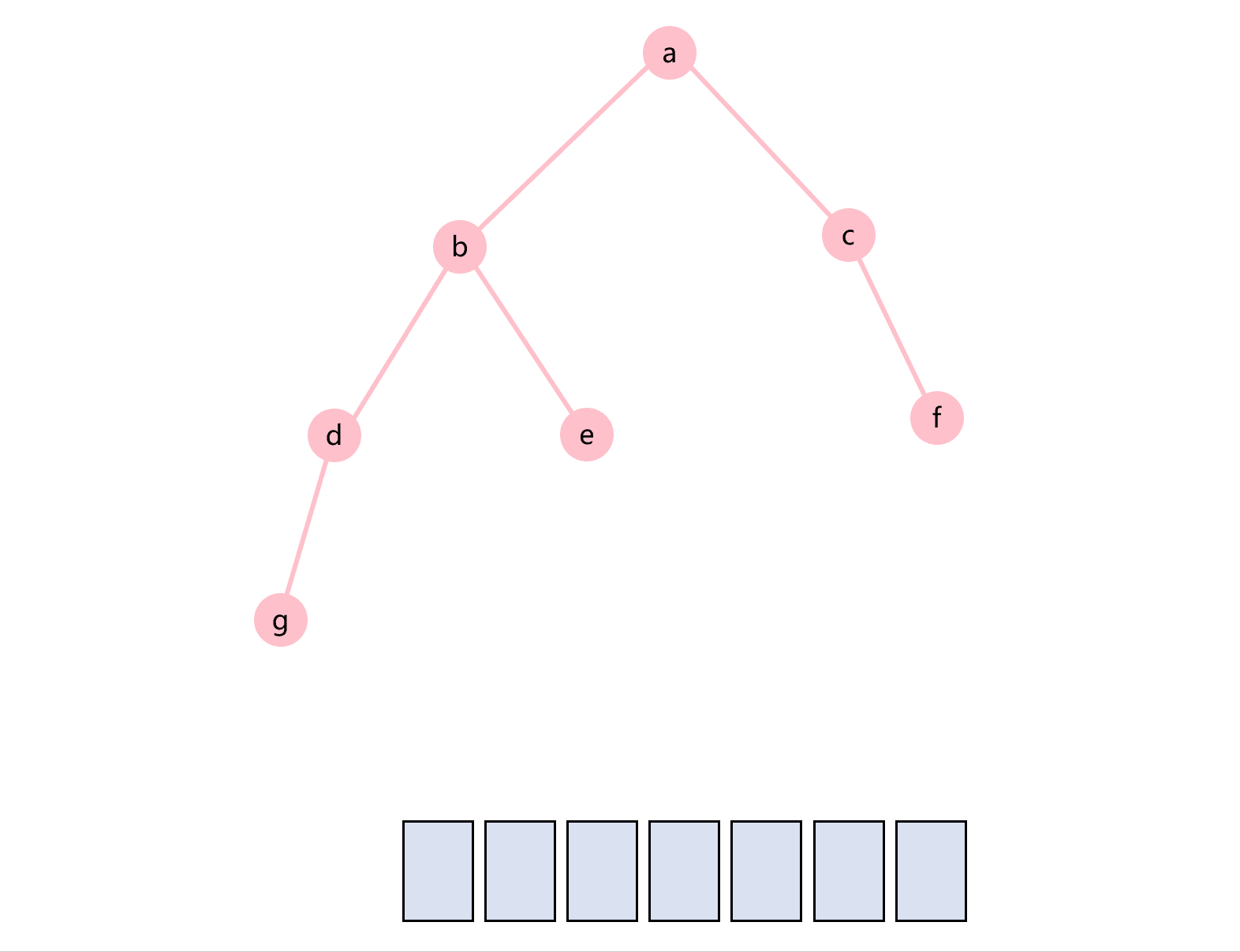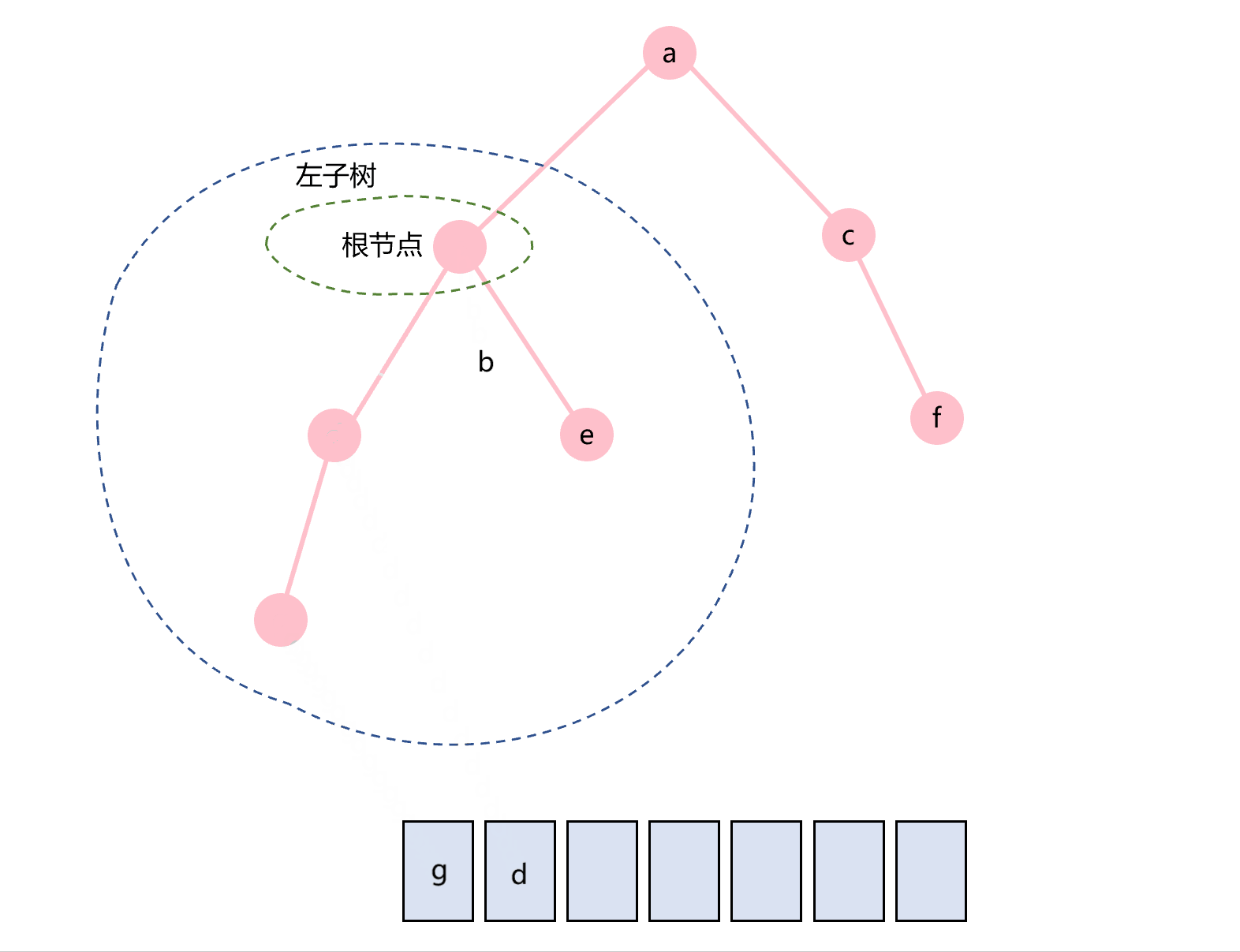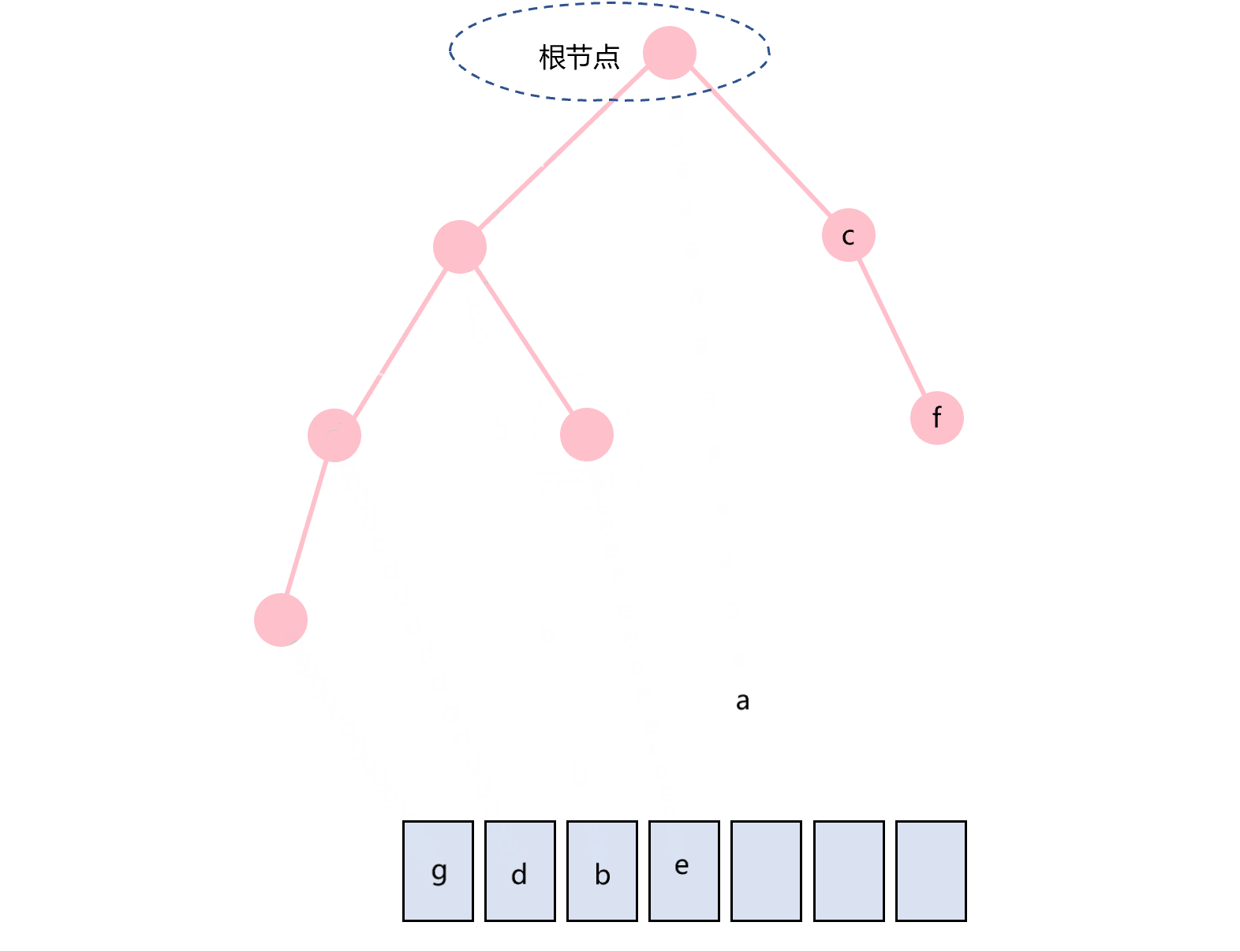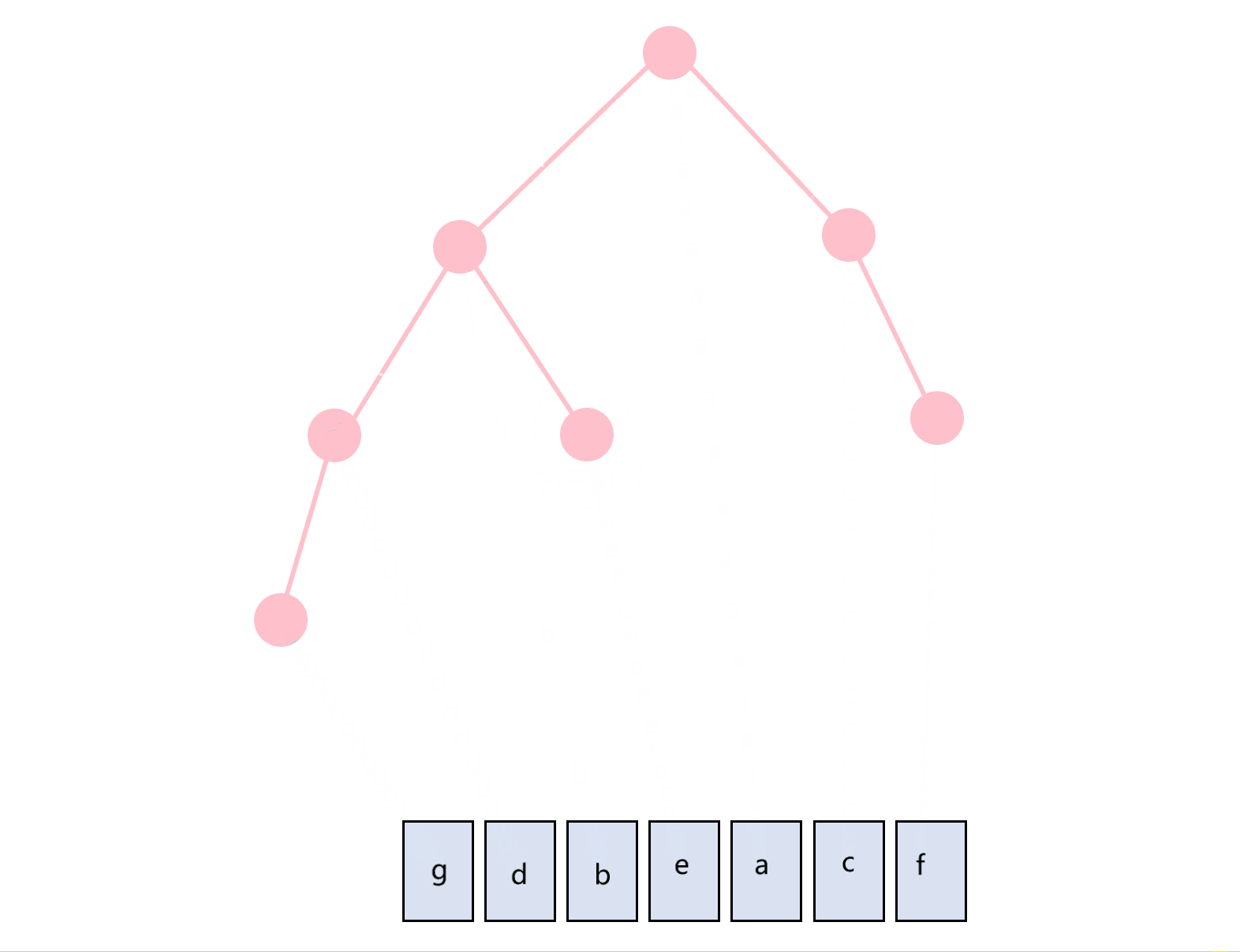
图3.3 中序遍历示意图

递归算法实现中序遍历的算法如下所示：

nodes=[]
def inorderTraverse(node):
    if node:
        inorderTraverse(node.left)
        nodes.append(node.val)
        inorderTraverse(node.right)
inorder traverse

那么，显然地，如果想要按照右子树-根节点-左子树的顺序遍历二叉树，只需要更改递归算法里面的left和right的顺序就可以了。同样地，不使用递归的话，中序遍历也是用栈和循环来实现的。只要不断地将当前的二叉树push到栈中，指针指向左子树，直到左子树为null，然后从栈中pop一棵二叉树，记录其根节点的值，并将指针指向右子树。整个过程如图3.4所示，代码如下：

图3.4 使用栈实现中序遍历示意图

nodes=[]
stack=[]
def inOrderTraverse(node):
    while node or len(stack)!=0:
        if node:
            stack.append(node)
            node=node.left
        else:
            node=stack.pop()
            nodes.append(node.val)
            node=node.right
inorder traverse

除此之外，Morris中序遍历算法能够实现空间复杂度为O(1)二叉树遍历，其核心思想是用时间换空间。第一次遍历时把当前二叉树的左子树的最右右子树指向当前二叉树，形成环。第二次遍历的时候，就可以回到根节点，并把环取消，如图3.5所示。代码如下： 

图3.5 Morris中序遍历

nodes=[]
def morrisTraverse(node):
    p1=node
    p2=None
    
    while p1:
        if p1.left:
            p2=p1.left
            while p2.right and p2.right!=p1:
                p2=p2.right
            
            if p2.right is None:
                p2.right=p1
                p1=p1.left
            else:
                nodes.append(p1.val)
                p2.right=None
                p1=p1.right
        else:
            nodes.append(p1.val)
            p1=p1.right
morris traverse

3.3.后序遍历

后序遍历的顺序是根节点在最后，即：左子树-右子树-根节点。同样地，递归算法很容易实现，并且也可以很容易地实现右子树-左子树-根节点的顺序遍历。递归算法代码如下：

 

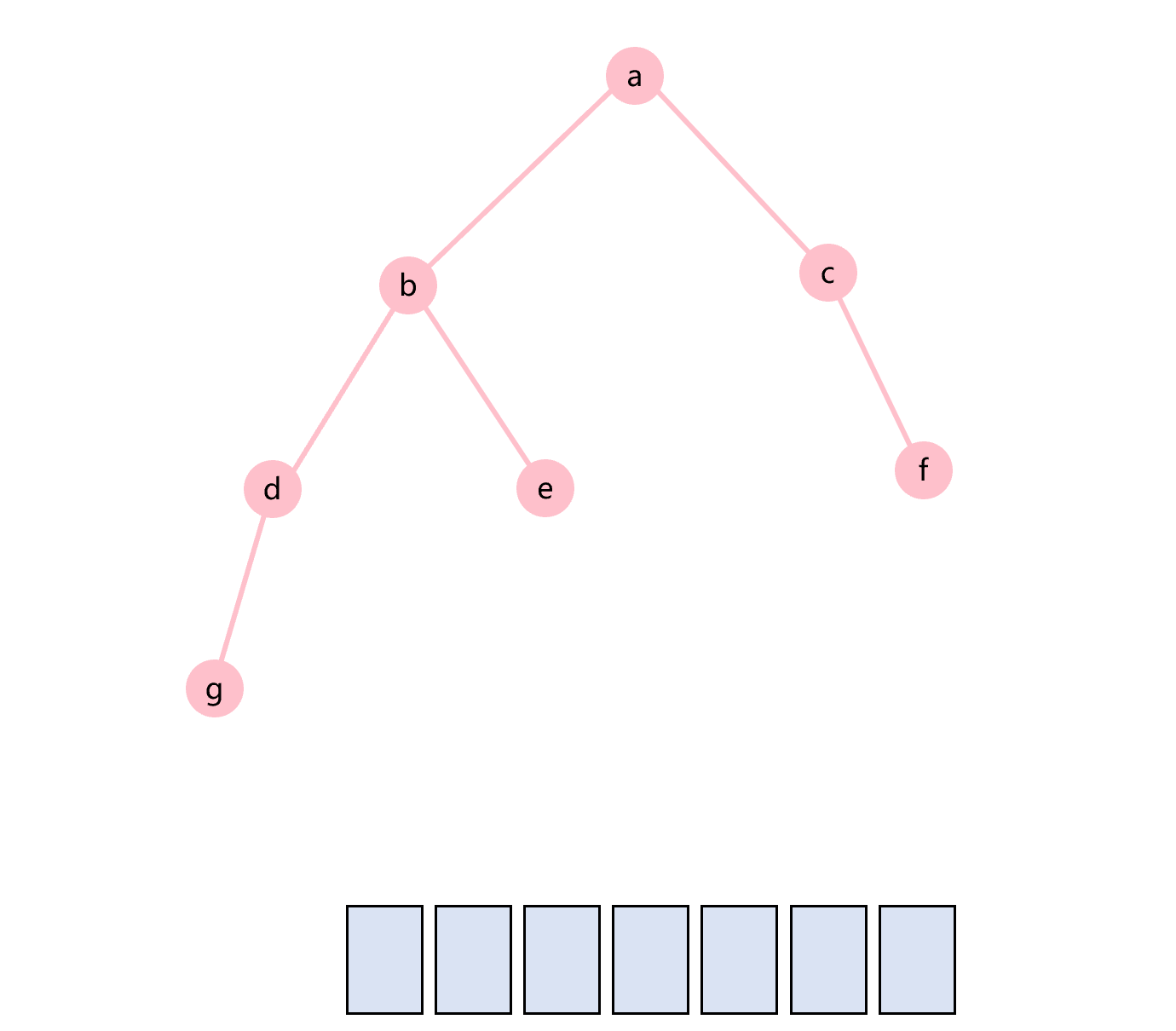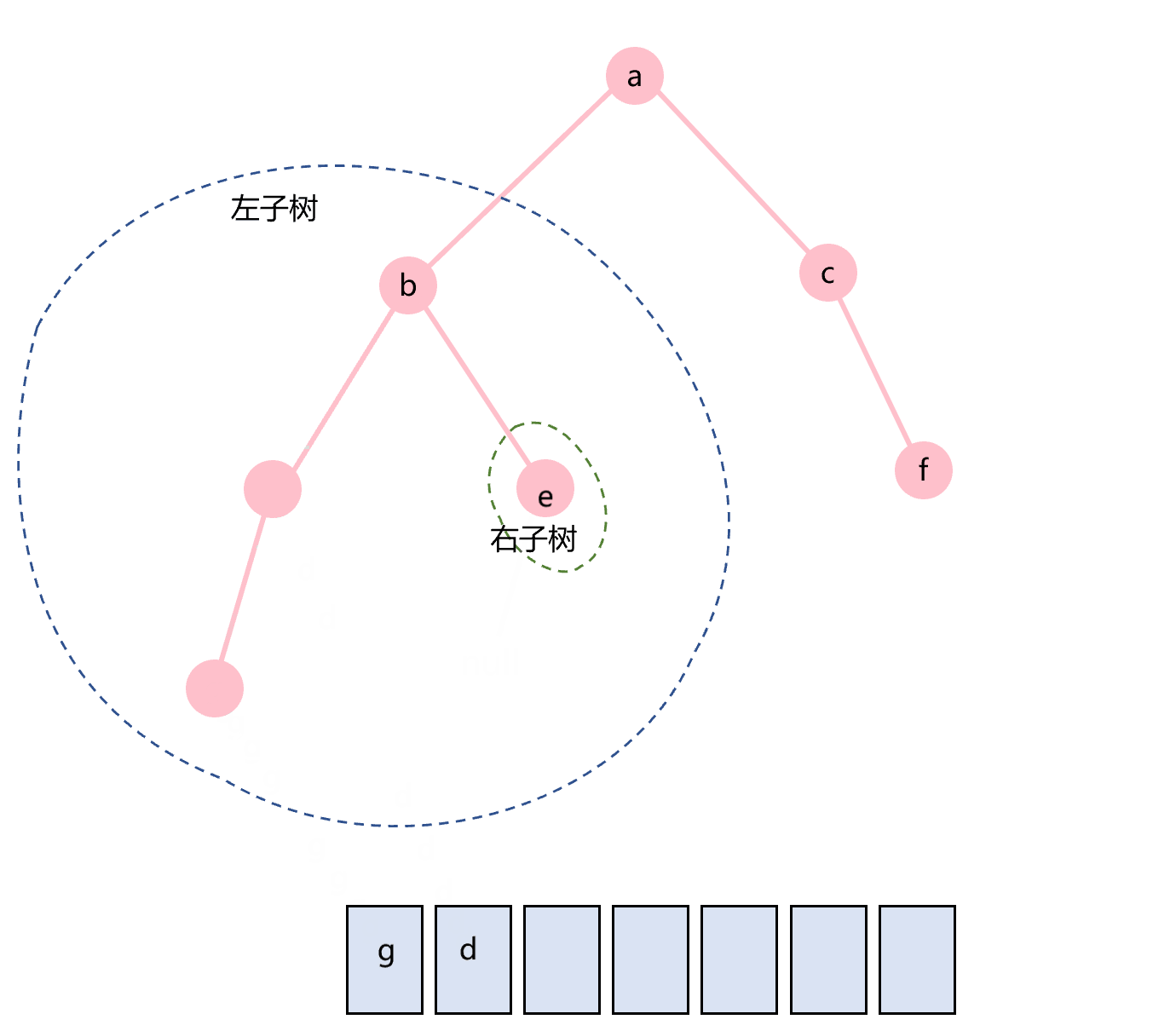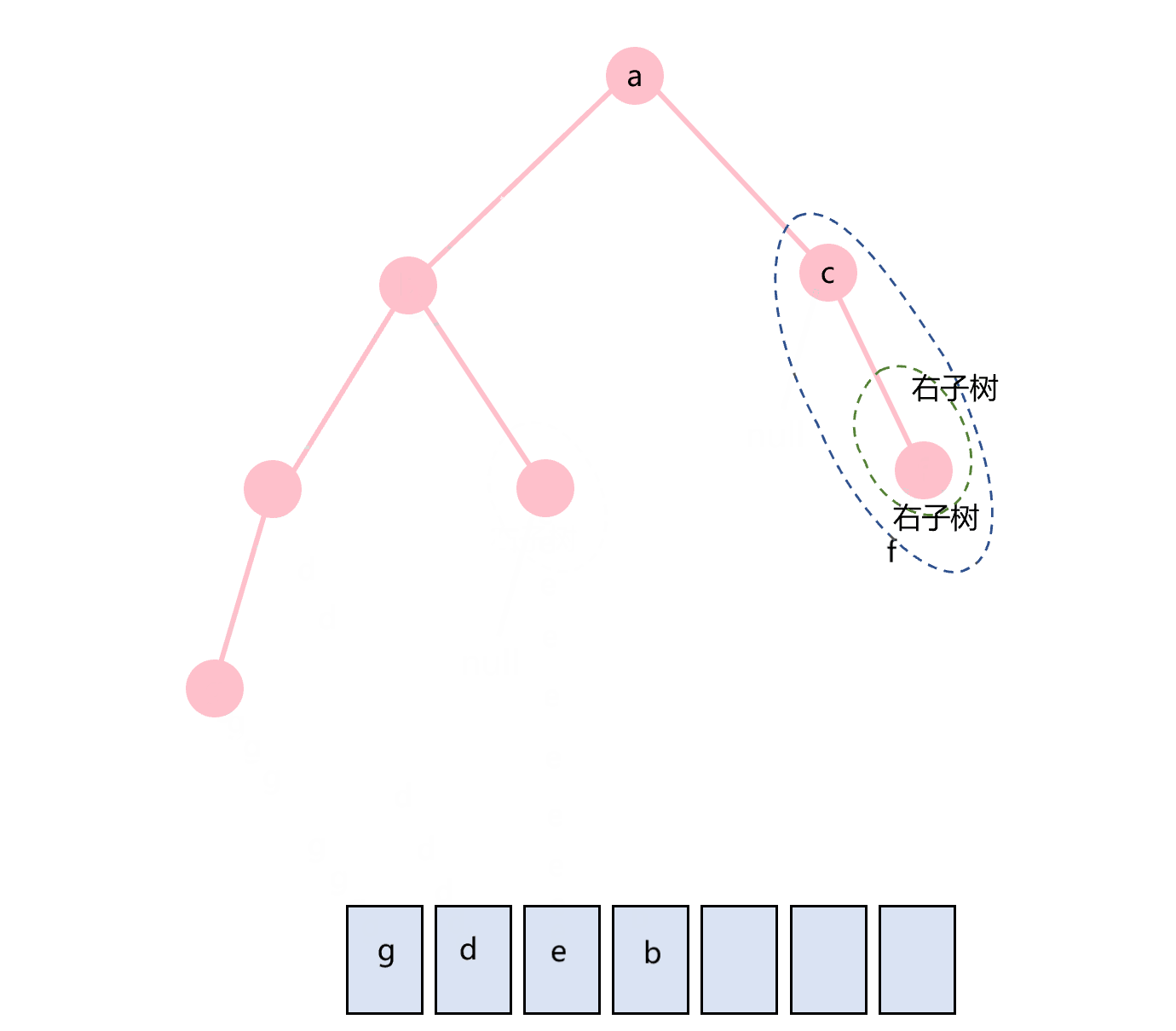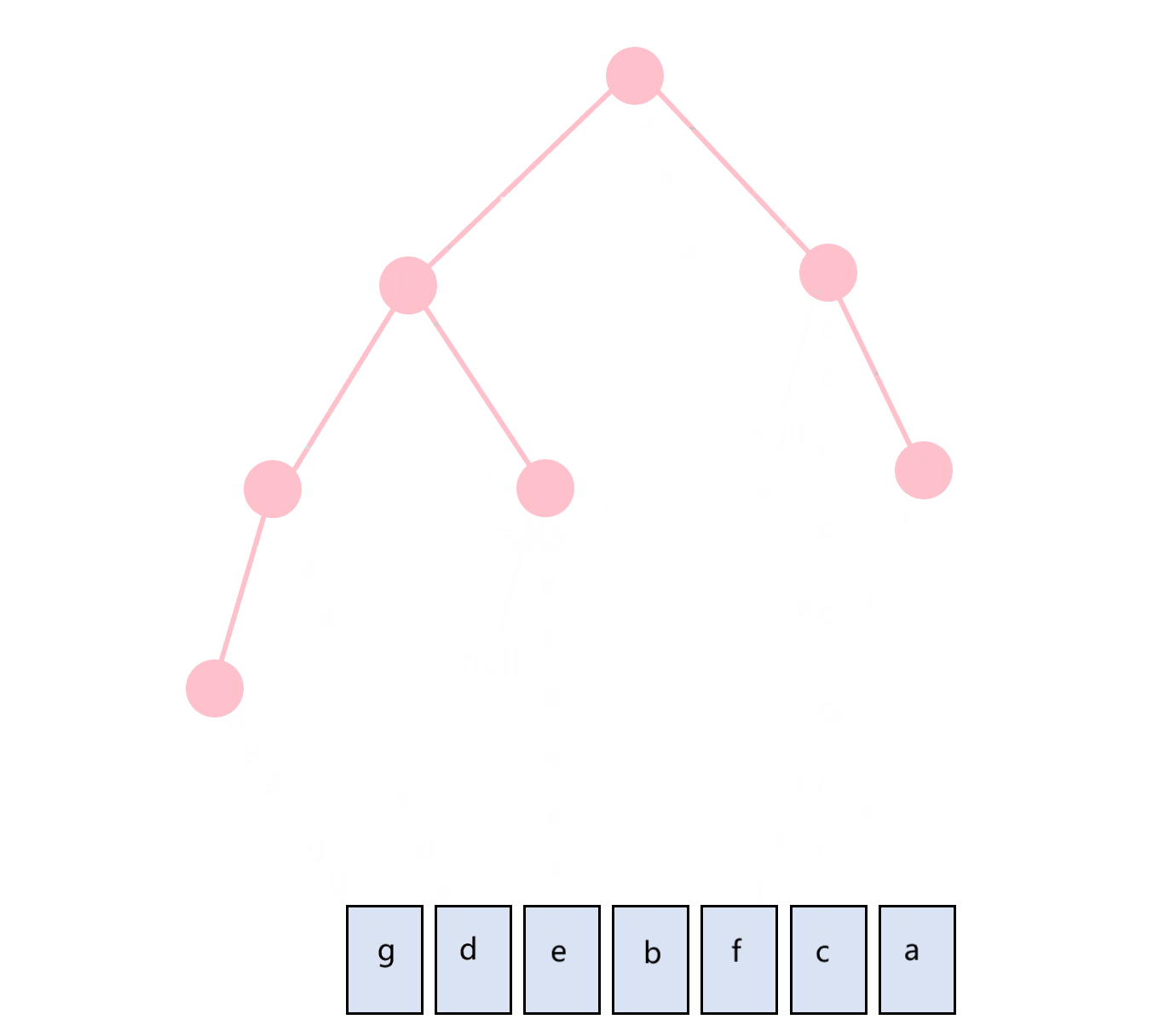
图3.6 后序遍历示意图

nodes=[]
def postorderTraverse(node):
    if node:
        postorderTraverse(node.left)
        postorderTraverse(node.right)
        nodes.append(node.val)
postorder traverse

同样地，后序遍历也可以用栈和循环来实现，这里记录的是我自己想的方法，可能跟其他的不太一样。把当前二叉树的根节点push进栈，如果其右子树不为null的话，把其右子树也push进栈，指针指向其左子树。当左子树为null时，从栈中pop元素，如果该元素的属性是二叉树，则重复循环，否则就意味着是根节点的值，记录即可。

 

 

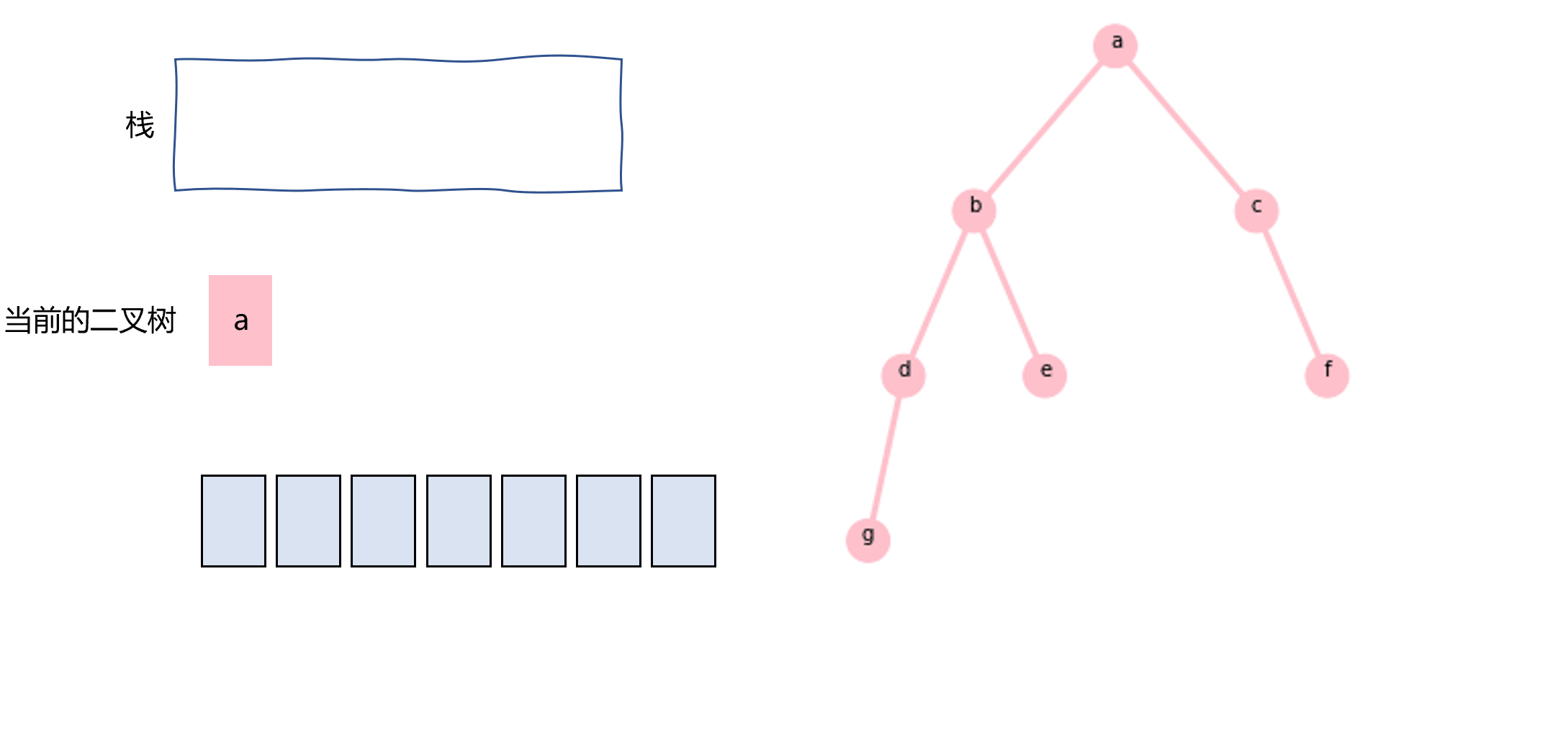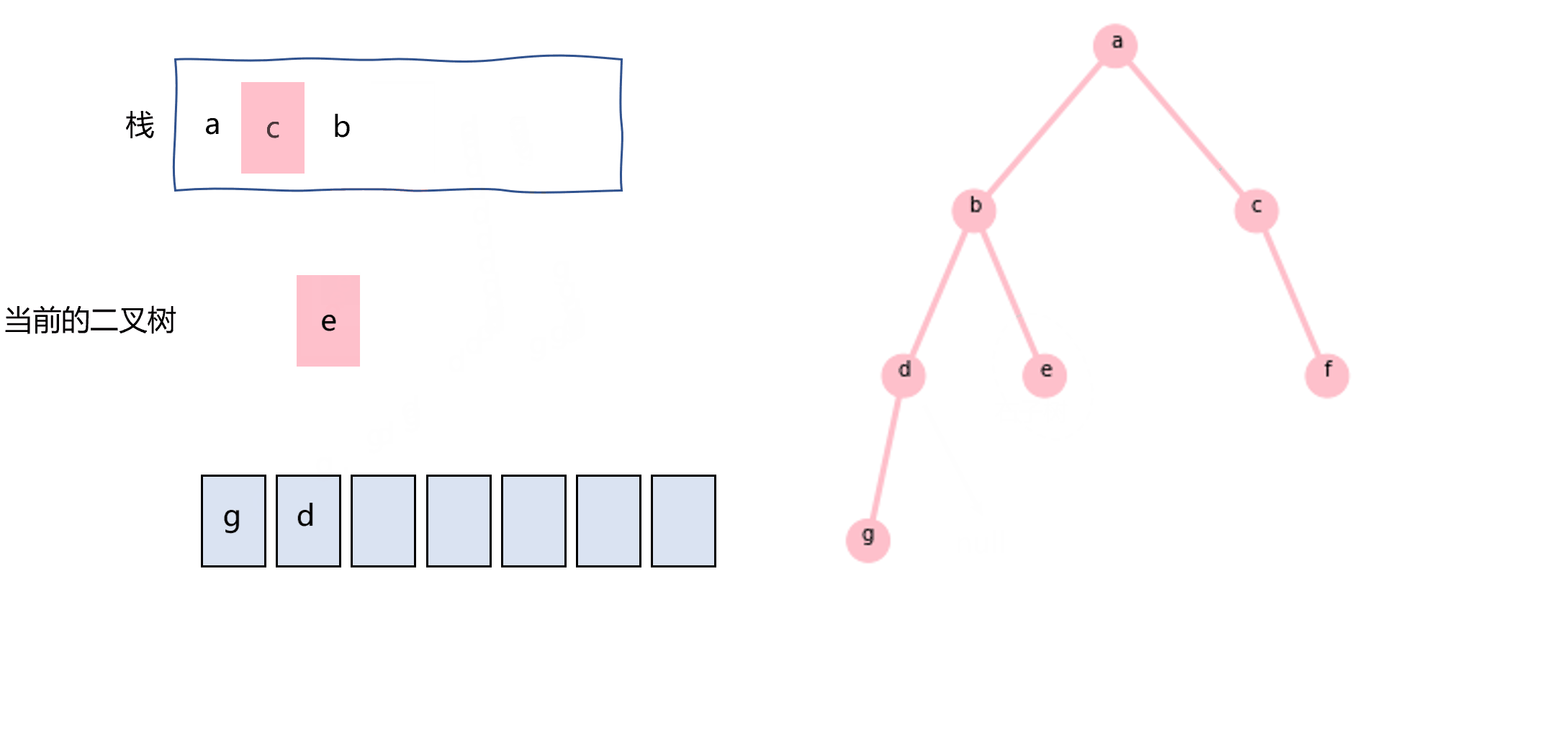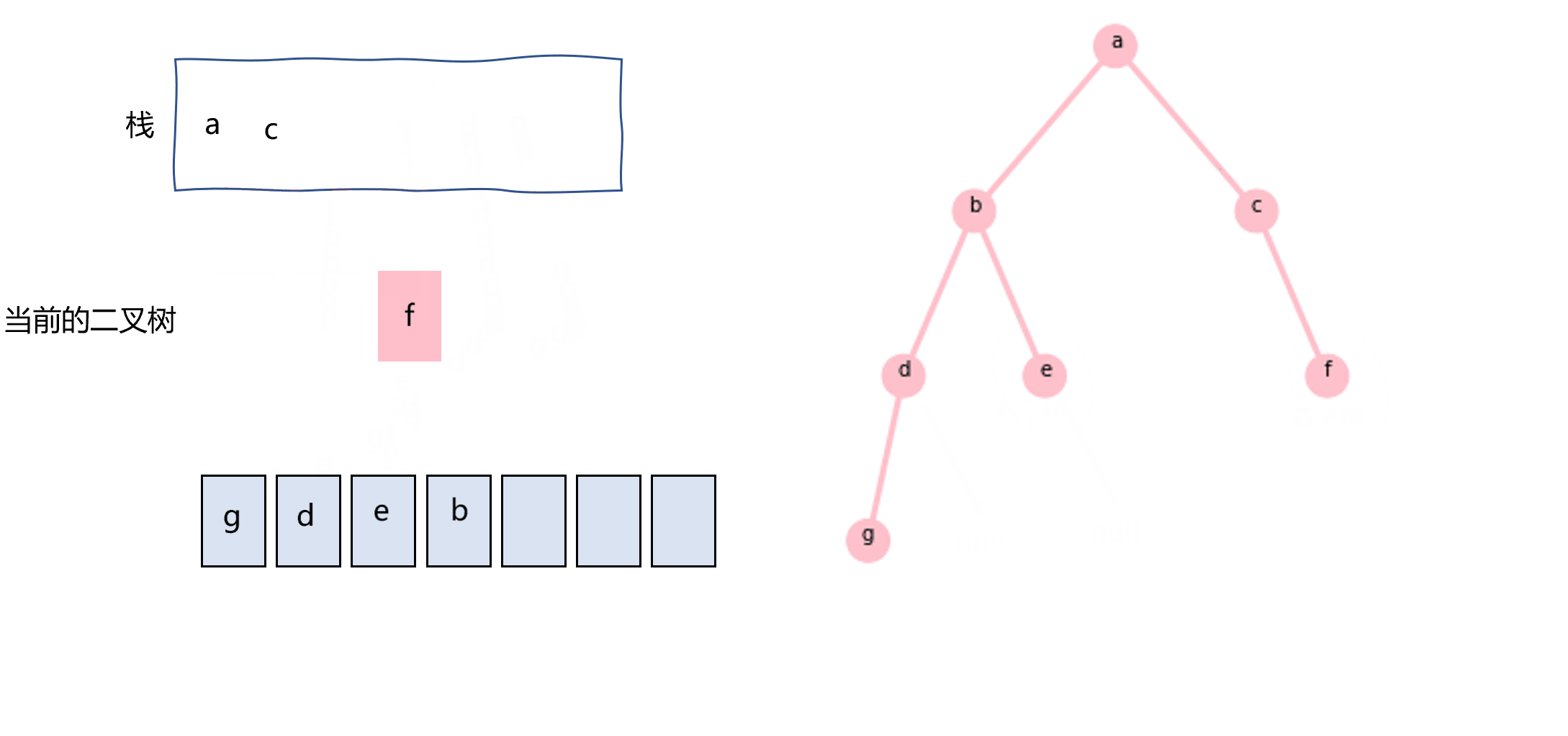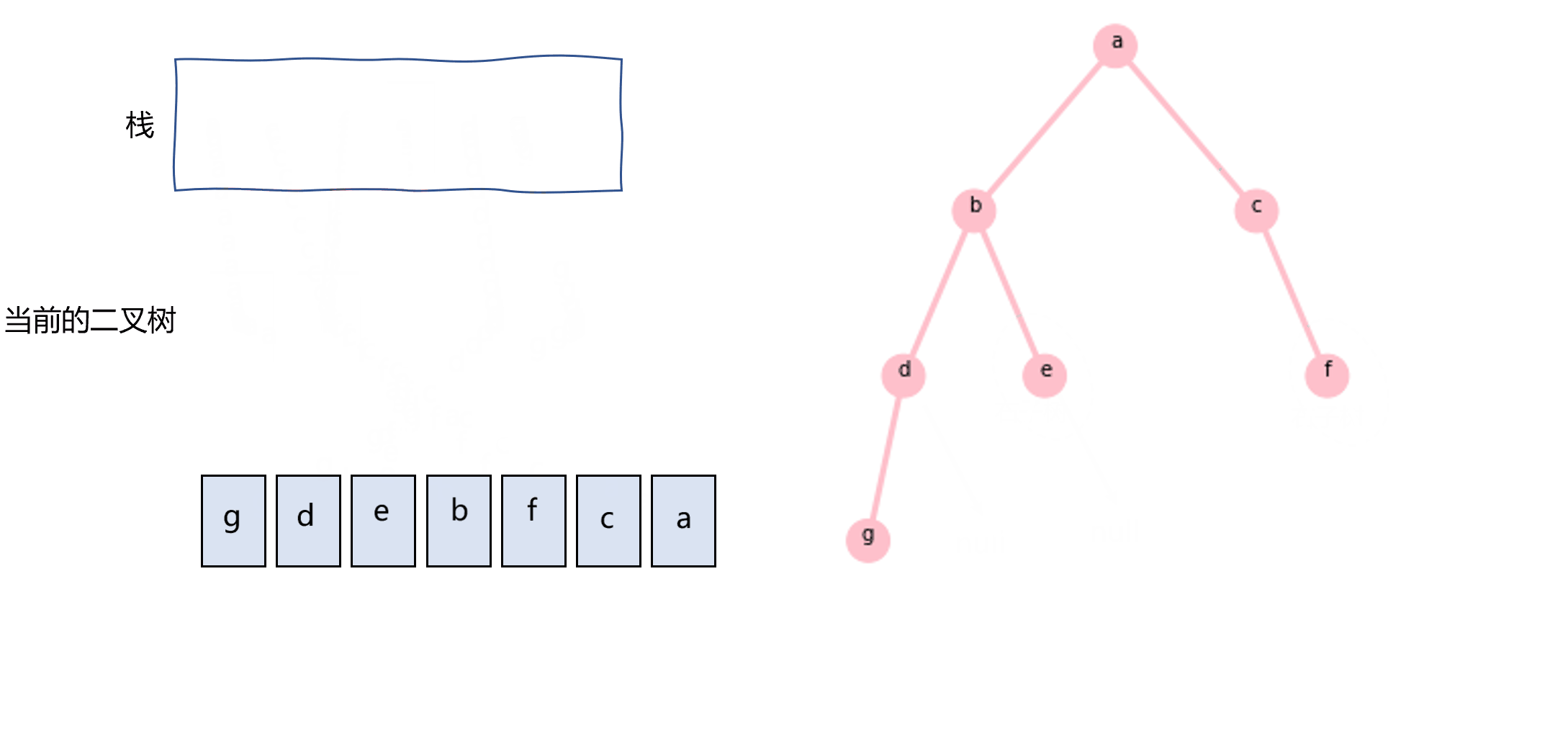
图3.7 使用栈实现后序遍历示意图

在leetcode关于二叉树的题目中，有的是给出前序遍历、中序遍历或者后序遍历中的两种，还原二叉树。这个还原的过程也可以使用递归。

  • 前序遍历的数组结构为：[根节点]+[左子树的节点]+[右子树的节点]
  • 中序遍历的数组结构为：[左子树的节点]+[根节点]+[右子树的节点]
  • 后序遍历的数组结构为：[左子树的节点]+[右子树的节点]+[根节点]

对于图片1所示的二叉树而言：

  • 前序遍历的结果：pre=[a,b,d,g,e,c,f]
  • 中序遍历的结果：in=[g,d,b,e,a,c,f]
  • 后序遍历的结果：post=[g,d,e,b,f,c,a]

以给出的是前序遍历和中序遍历数组为例。前序遍历数组的第一个元素是二叉树根节点的值，即a。在中序遍历中，a的索引是4，则in[0:4]是二叉树的左子树的中序遍历的结果，in[5:]是二叉树的右子树的中序遍历的结果。那么pre[1:5]是二叉树的左子树的前序遍历的结果，pre[5:]是二叉树的右子树的前序遍历的结果。pre[1:5]和in[0:4]作为输入，则可以返回左子树，pre[5:]和in[5:]作为输入，则可以返回右子树。

3.4.层次遍历

层次遍历就是一层层的输出二叉树的节点，如图3.8所示。

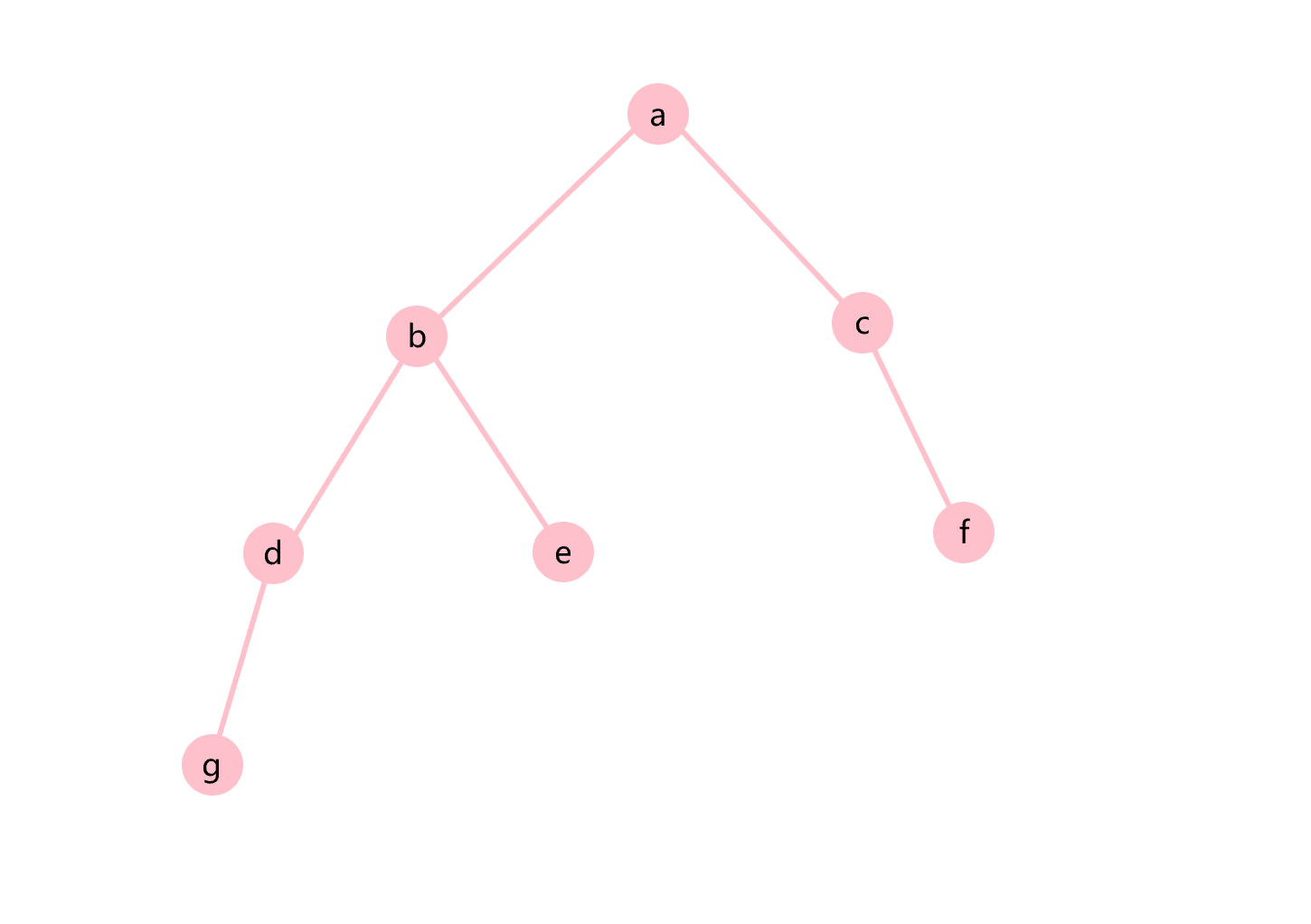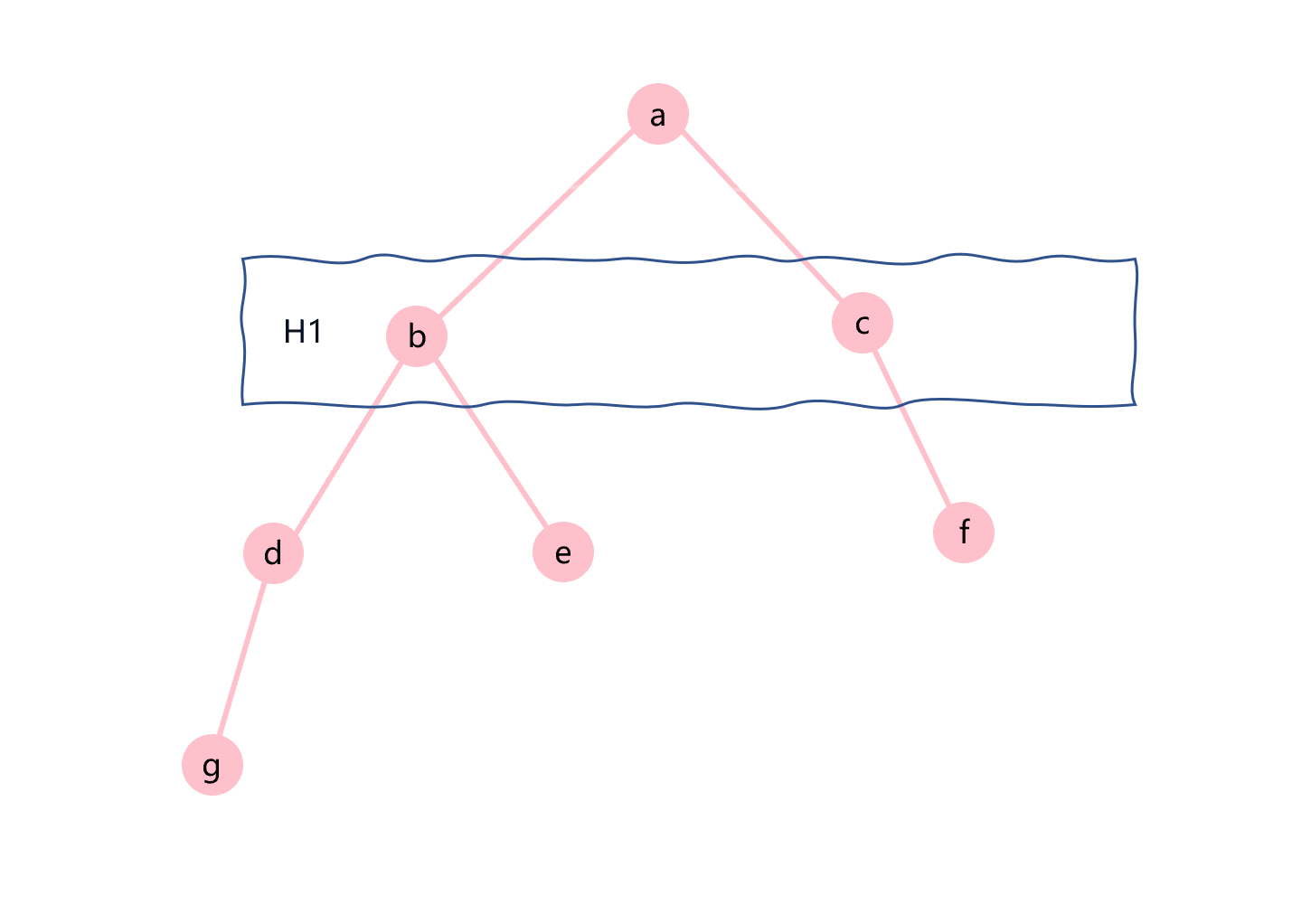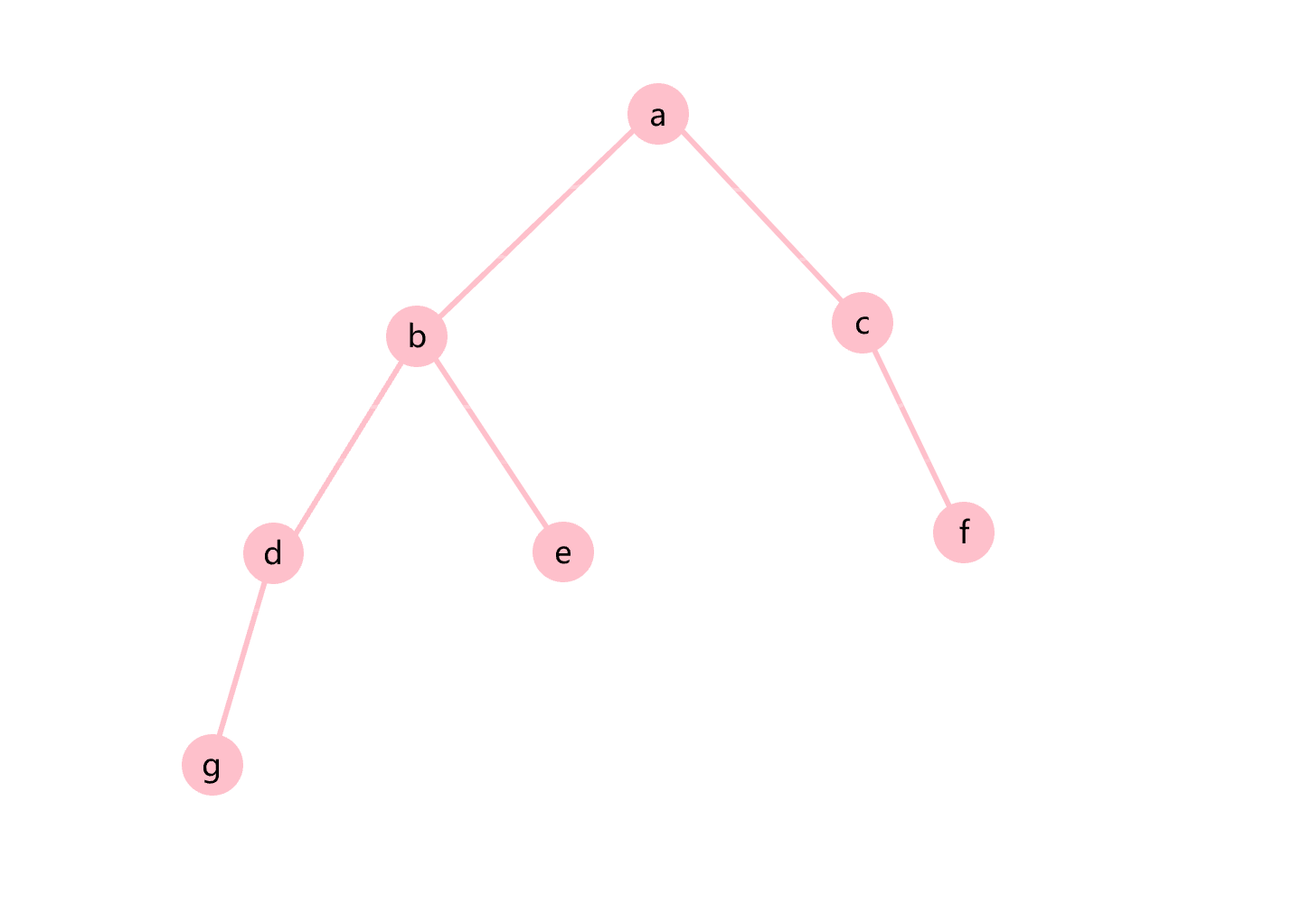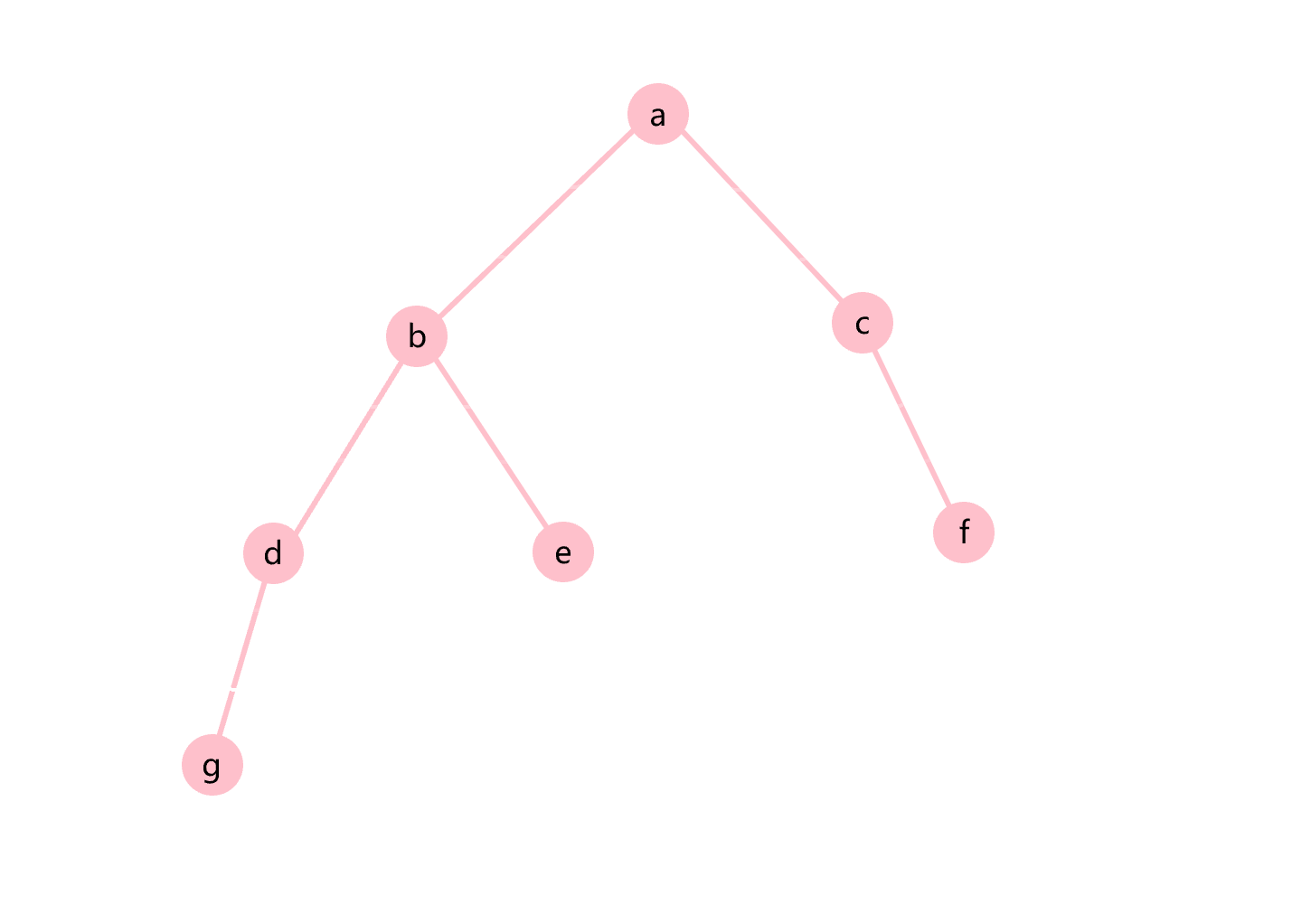
图3.8 层次遍历示意图

层次遍历一般用队列实现，如图3.9所示，代码如下所示：

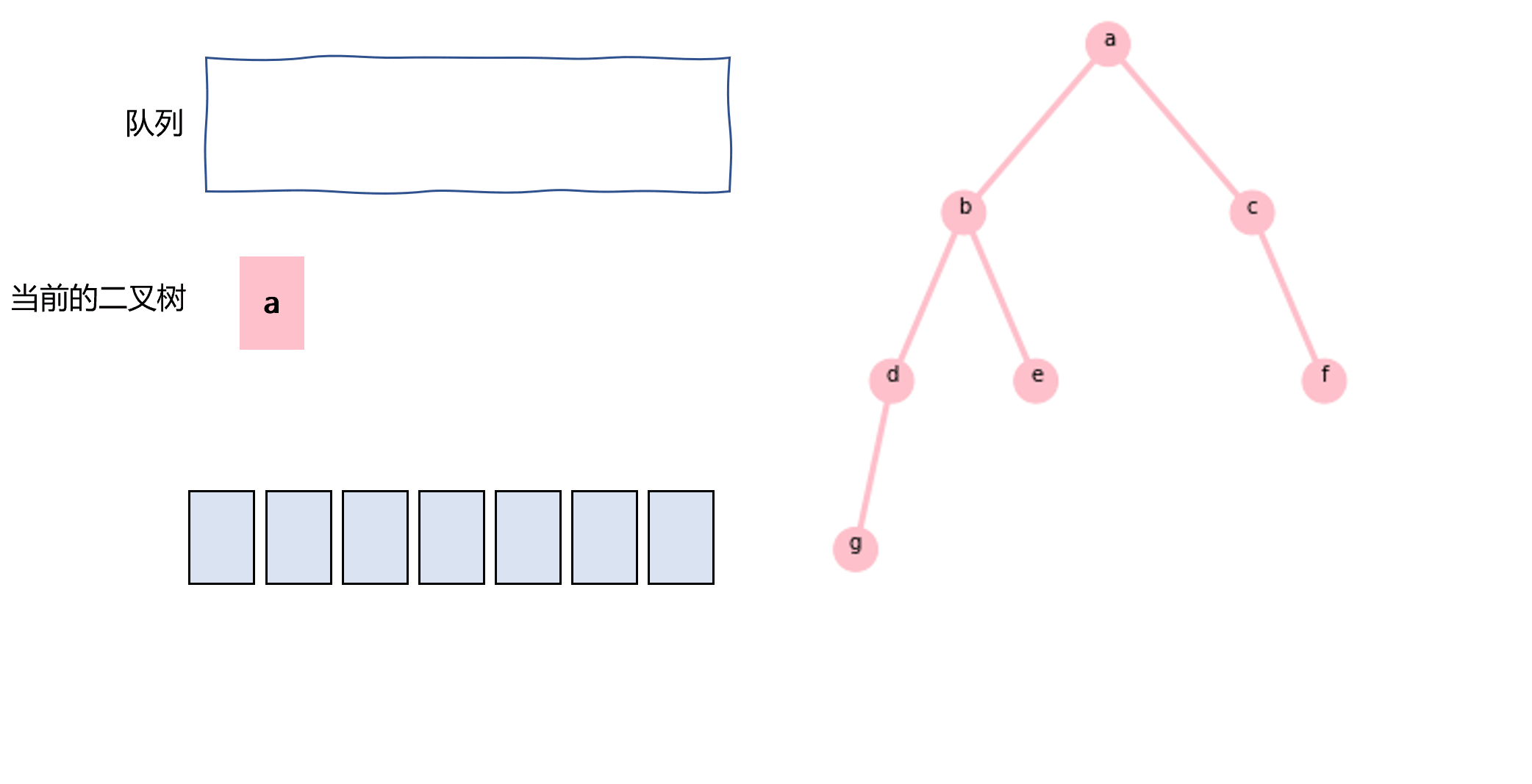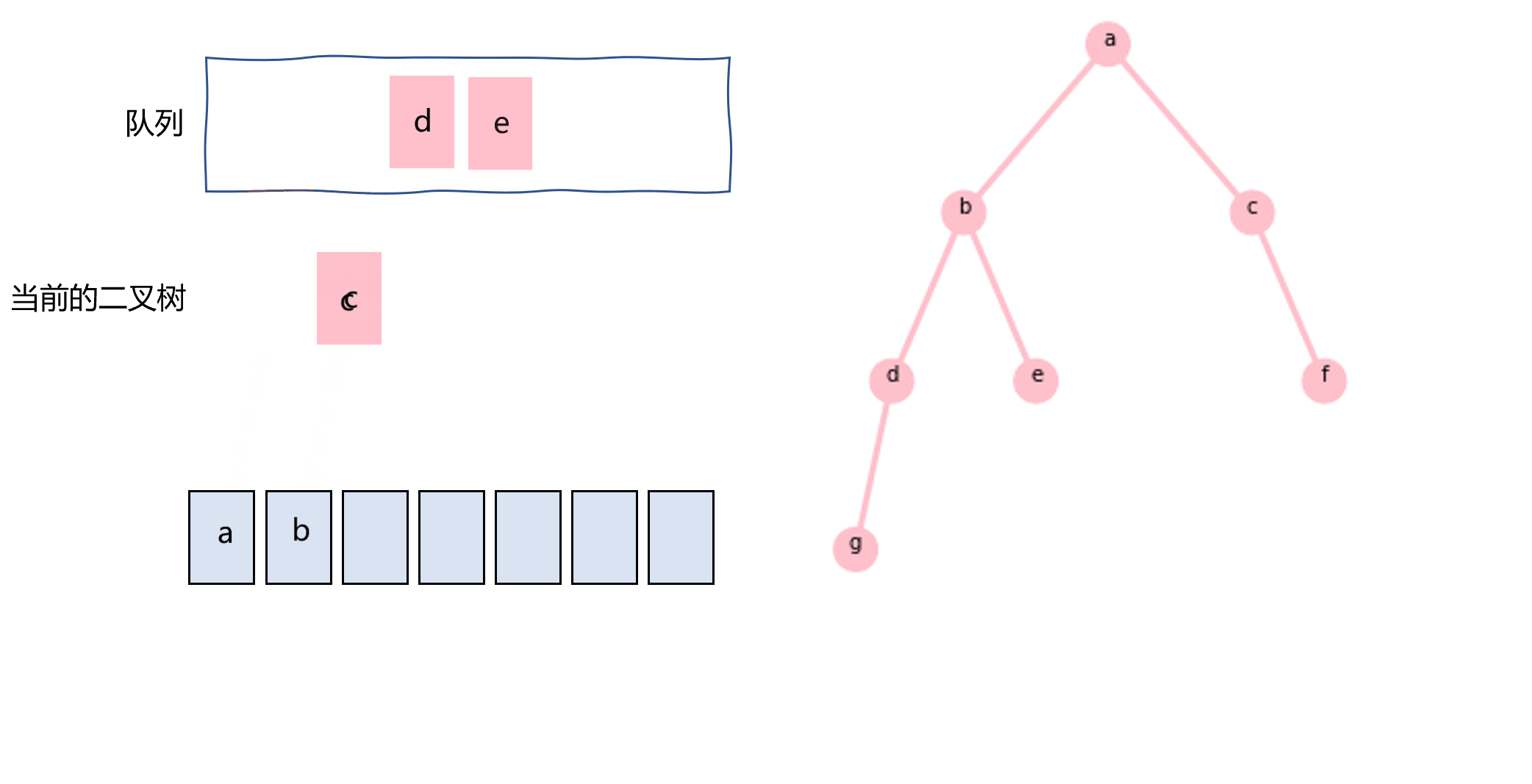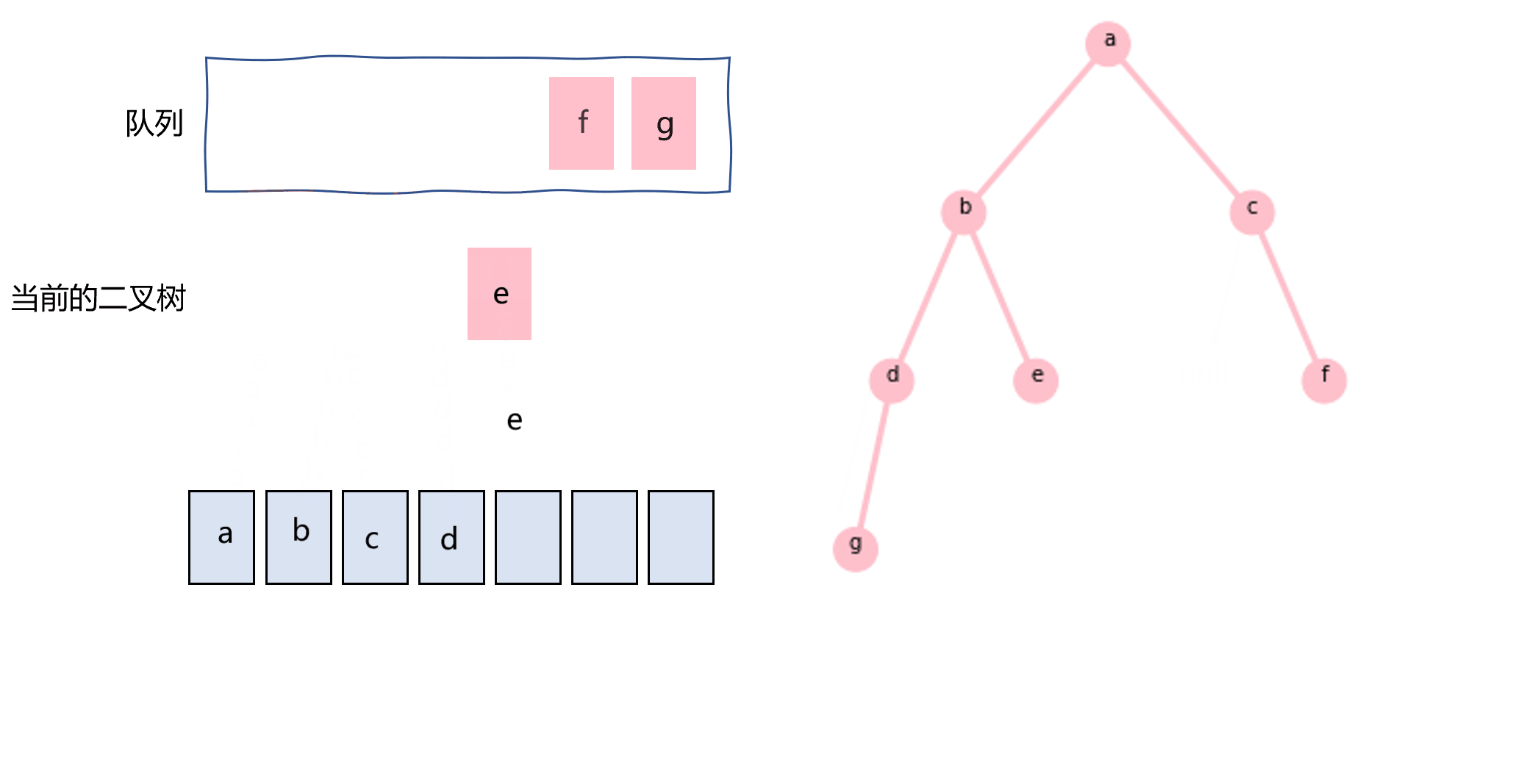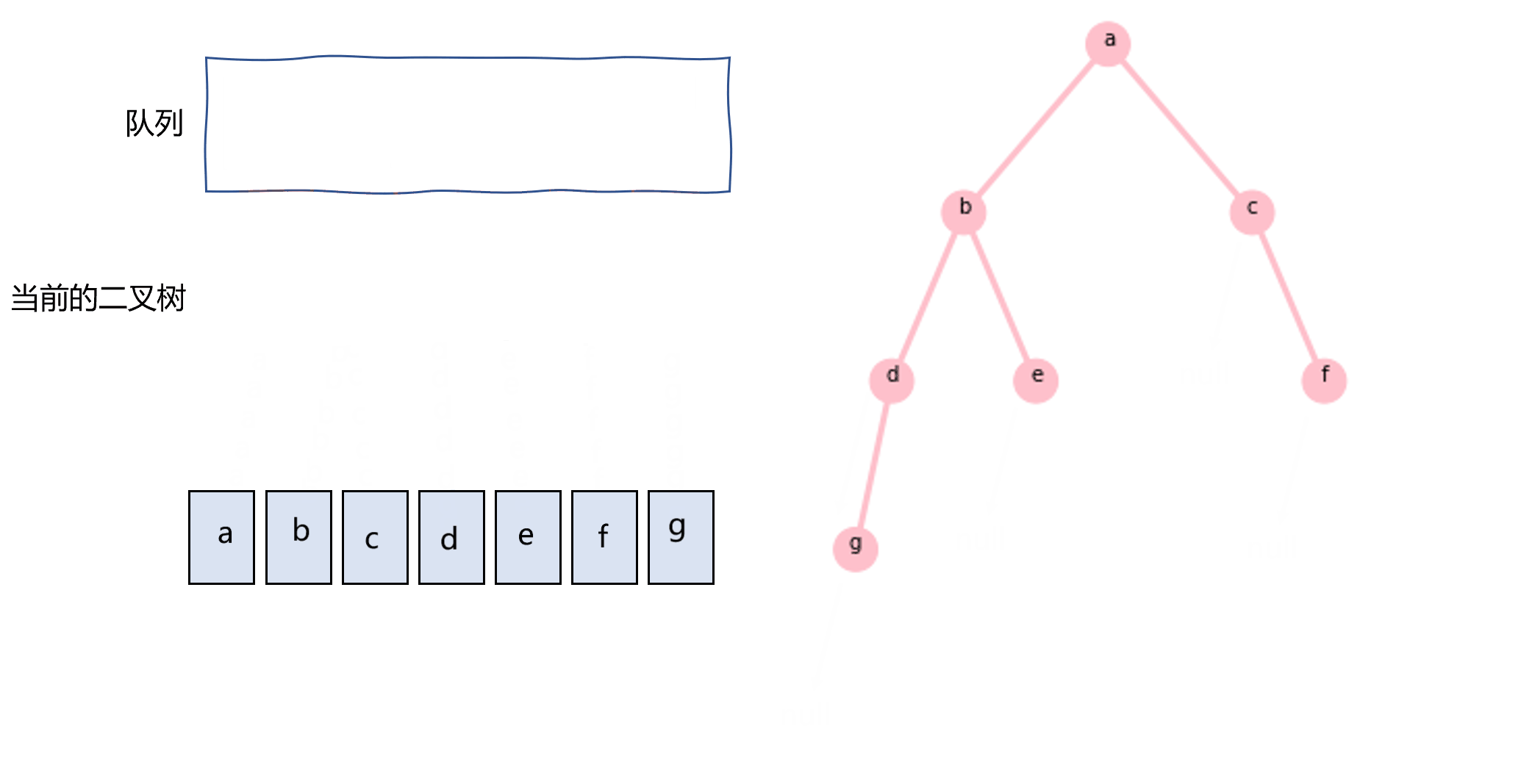
图3.9 使用队列实现层次遍历示意图

def layertraverse(node):
    nodes=[]
    queue=[node]
    while len(queue)!=0:
        _node=queue.pop(0)
        nodes.append(_node.val)
        if _node.left:
            queue.append(_node.left)
        if _node.right:
            queue.append(_node.right)
    return nodes
layer traverse

在层次遍历的题目中，有的要求是每一层每一层的输出，即[[a],[b,c],[d,e,f],[g]]这样的形式。一般我会增加一个队列的长度的参数用来分层。此外，还有要求zigzag样式的输出，即[[a],[c,b],[d,e,f],[g]]这种也比较简单。层次遍历的题目都相对比较简单。

4.二叉树的应用

4.1.二叉搜索树(binary search tree, BST)

二叉树这种数据结构的应用必然是依赖于其“二叉”的特点的，即二分。二叉搜索树的定义就是左子树的全部节点的节点值都小于根节点的值，右子树的全部节点的节点值都大于根节点的值，即：左子树<根节点<右子树。如图4.1所示。跟快速排序很像。

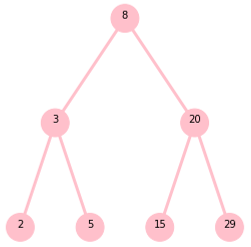
图4.1 二叉搜索树

可见，在一棵二叉搜索树中，最左边的节点值最小，最右边的节点值最大，并且中序遍历将得到一个升序数组。对于图4.1这棵二叉搜索树，如果想要查找2，则只需要在8的左子树和3的左子树里查找就可以了。

此外，leetcode上关于二叉搜索树的问题还有寻找一棵二叉搜索树中第k大节点的值的问题，也是可以中序遍历，直到输出第k大节点就可以中止循环了。还有一些题目是修剪、修复二叉搜索树等，解题的思路都是建立在熟练掌握二叉树的各种遍历方法和二叉搜索树的特点基础上。

值得一提的是，我感觉二叉搜索树中节点的值不一定非得是数字，即二叉搜索树满足的条件不一定是左子树的节点值都小于根节点的值。只要是符合某种左子树、根节点、右子树的条件都可以看作是二叉搜索树，比如图4.2这棵二叉树，可以表示字母和数字的摩尔斯电码。这里也能看出来了，二叉树搜索适用于数据量特别大的时候，像摩尔斯电码这种，辛辛苦苦构建一个二叉树，查找的速度跟列表也不差多少。

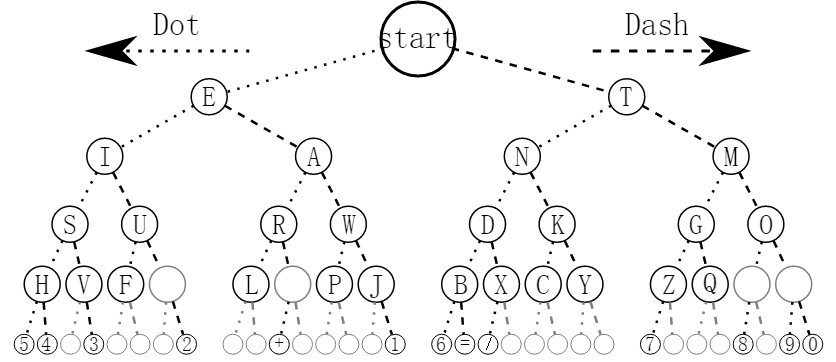
图4.2 莫尔斯电码二叉树

4.2.平衡二叉树

使用二叉搜索树的算法的运行时间取决于树的形状，而树的形状又取决于键被插入的先后顺序。这就可能会出现图4.3所示的情况，虽然也是一棵二叉搜索树，但是它已经跟链表没有什么区别了，时间复杂度从O(log2n)变成了O(n)。这是最坏的情况。例如同样查找2，就需要从29一路查找左子树下去。因此，为了更好的利用二分特点，就有了平衡二叉树，其定义是左右子树的高度差的绝对值不超过1。又根据提出平衡二叉树的数学家的名字命名，平衡二叉树也被称为AVL树。AVL类就是在二叉树的基础上增加了高度属性。

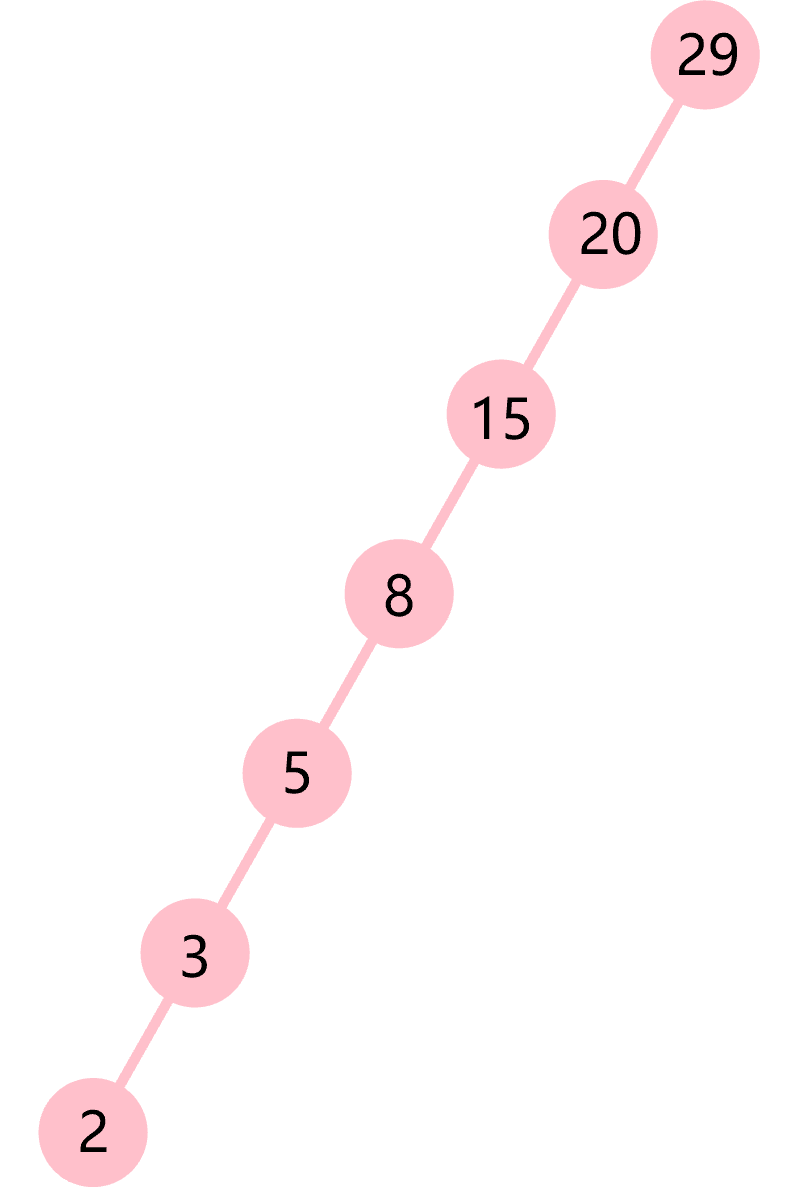
图4.3 一棵退化成链表的二叉搜索树

class AVLnode:
    def __init__(self,val,left=None,right=None,height=1):
        self.val=val
        self.left=left
        self.right=right
        self.height=height
AVL class

平衡因子(Balance Factor, BF)是指某个节点的左子树和右子树的高度差值。因此在一棵AVL树中，BF的值只能为-1,0,1。

在leetcode中，有一类平衡二叉树的问题是给出一棵非平衡二叉树，将其重构成平衡二叉树。例如将图16的这棵二叉搜索树重构为一棵平衡的二叉搜索树。看了一些题解，做法差不多都是先中序遍历，然后再递归重构平衡二叉树。

除重构外，插入和删除节点后旋转节点以保持高度的平衡性是平衡二叉树的重点所在。先来看下什么是节点的顺时针旋转(也称为右旋转)和逆时针旋转(也称为左旋转)。图4.4所示为Y节点的顺时针旋转，X节点的右子树变成Y节点的新左子树，构成了新二叉树成为X节点的新右子树。

 

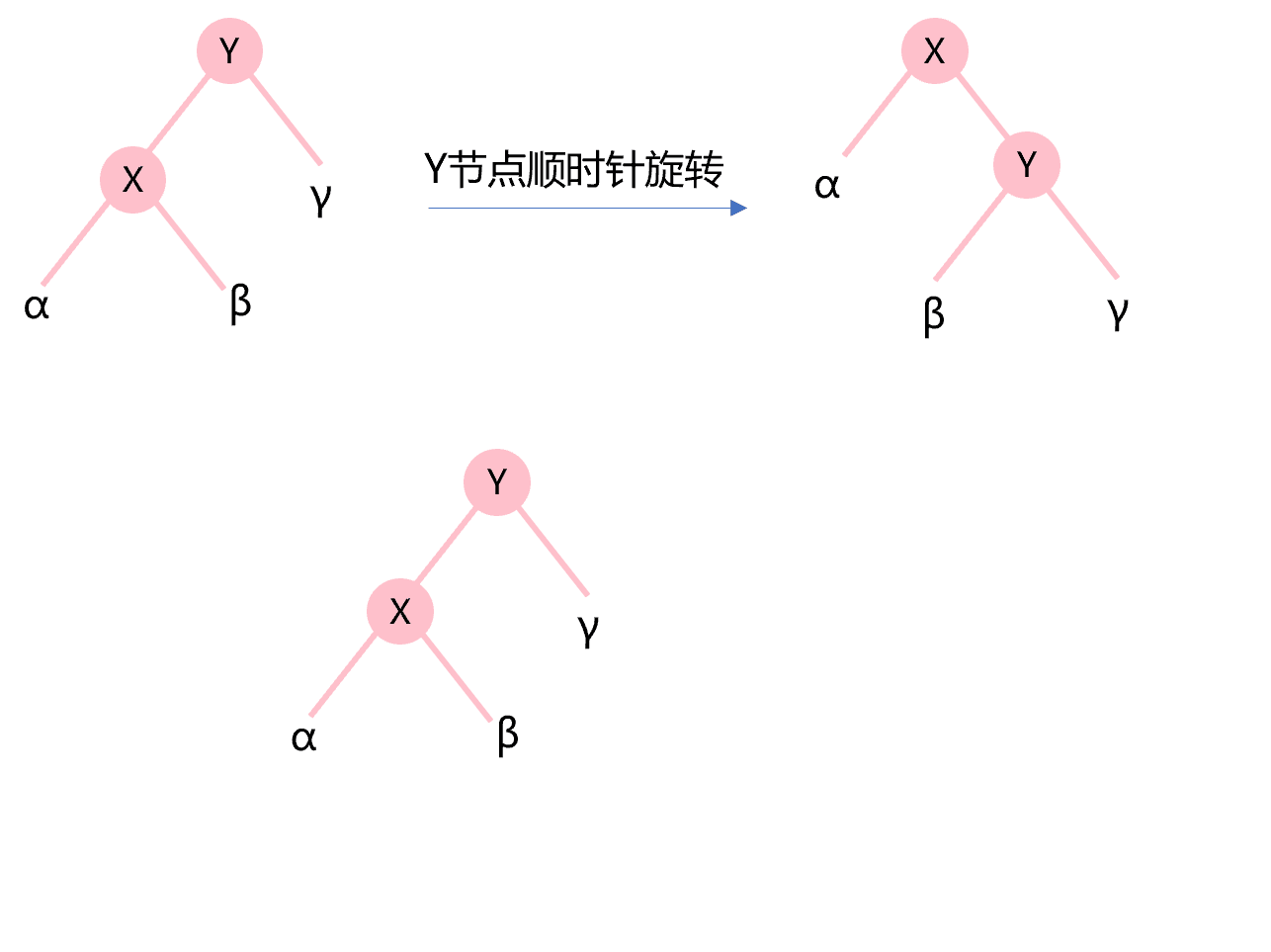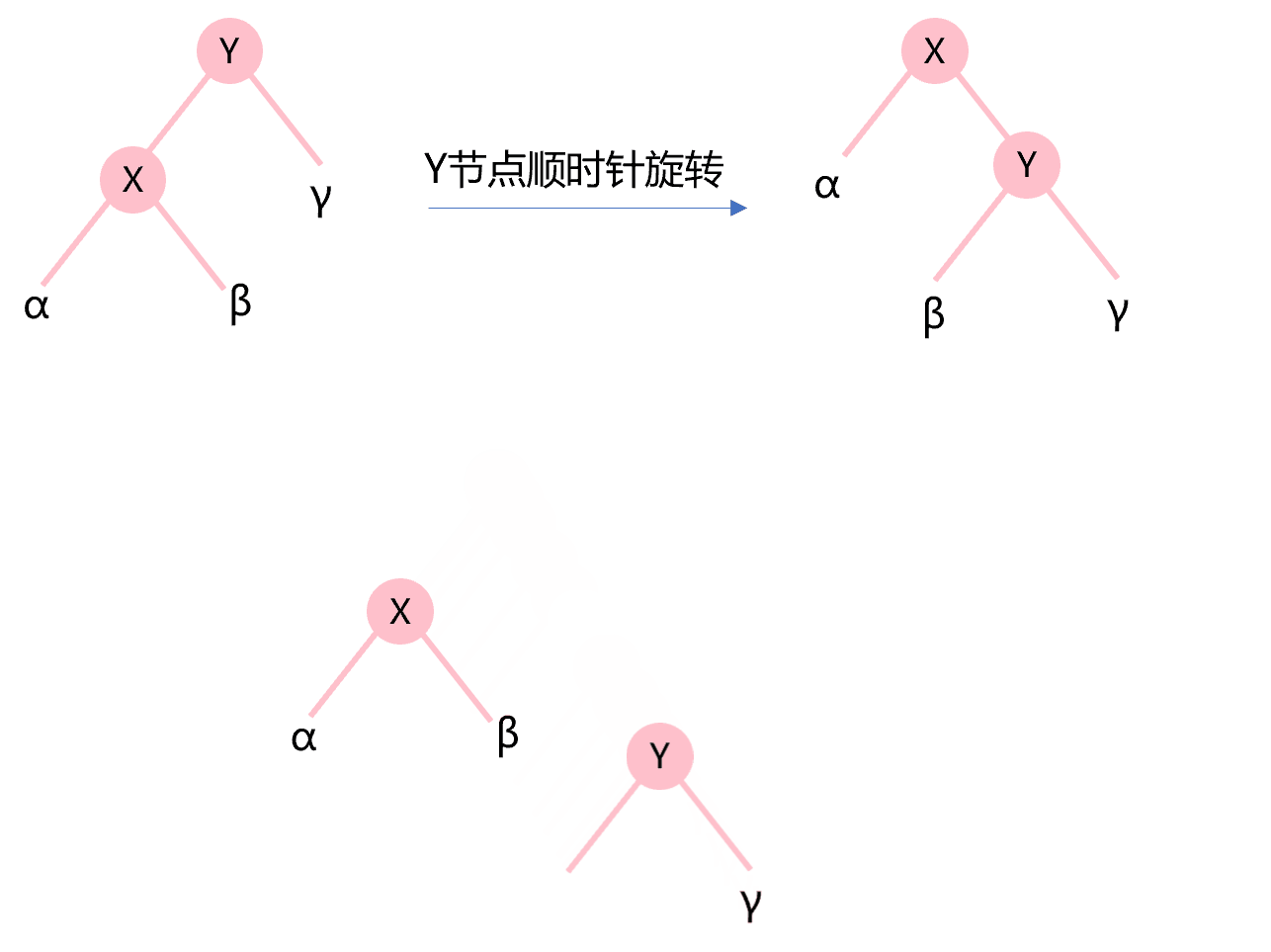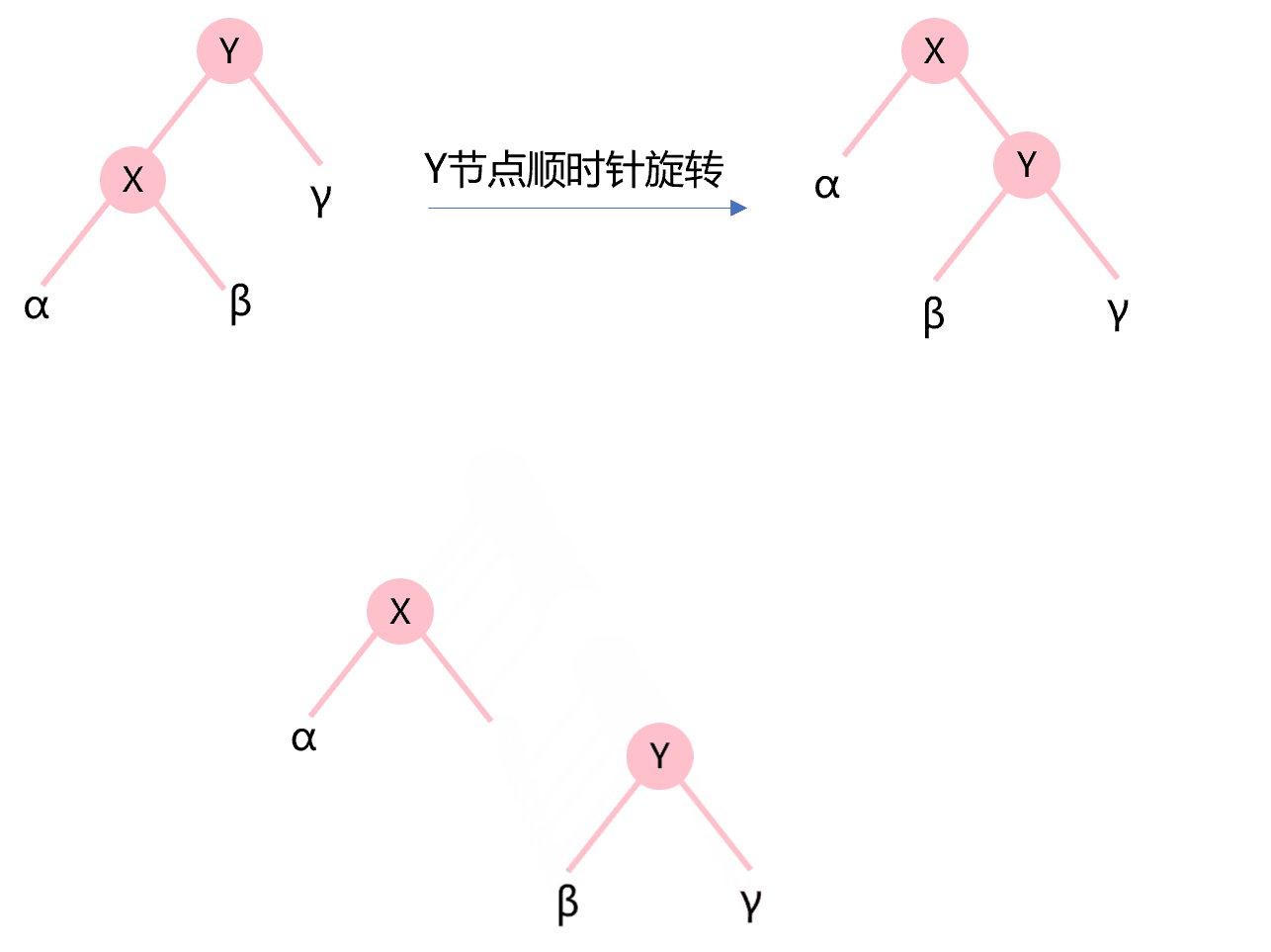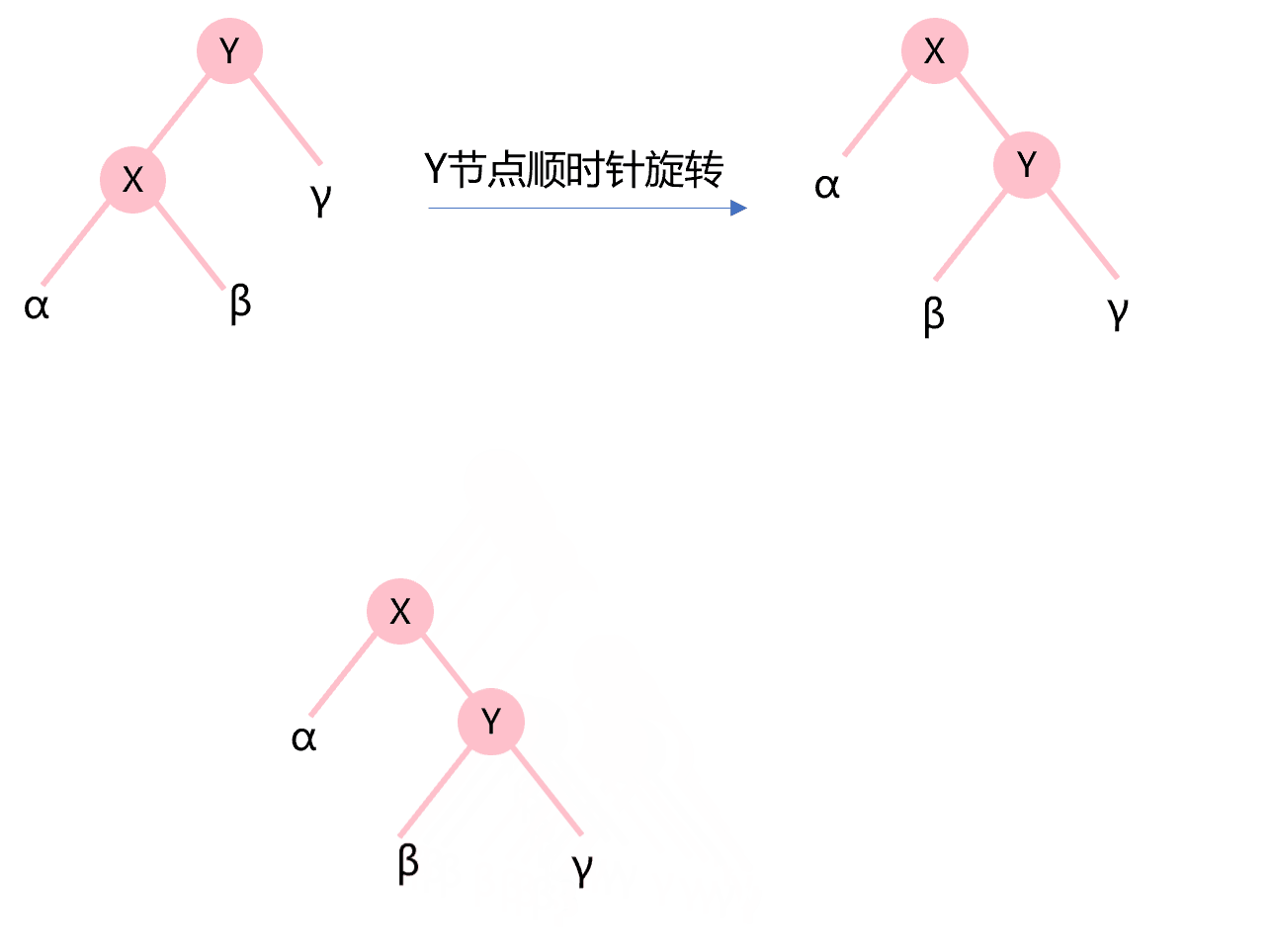
图4.4 节点顺时针旋转示意图

def rotateCW(self,node:AVLnode):
        left=node.left
        node.left=left.right
        left.right=node
                 node.height=1+max(self.height(node.left),self.height(node.right))
        left.height=1+max(self.height(left.left),self.height(left.right))
        return left
rotateCW

 类似地，图4.5所示为X节点的逆时针旋转。Y的左子树作为X的新右子树，构建成的新二叉树成为Y的新左子树。

 

 

 

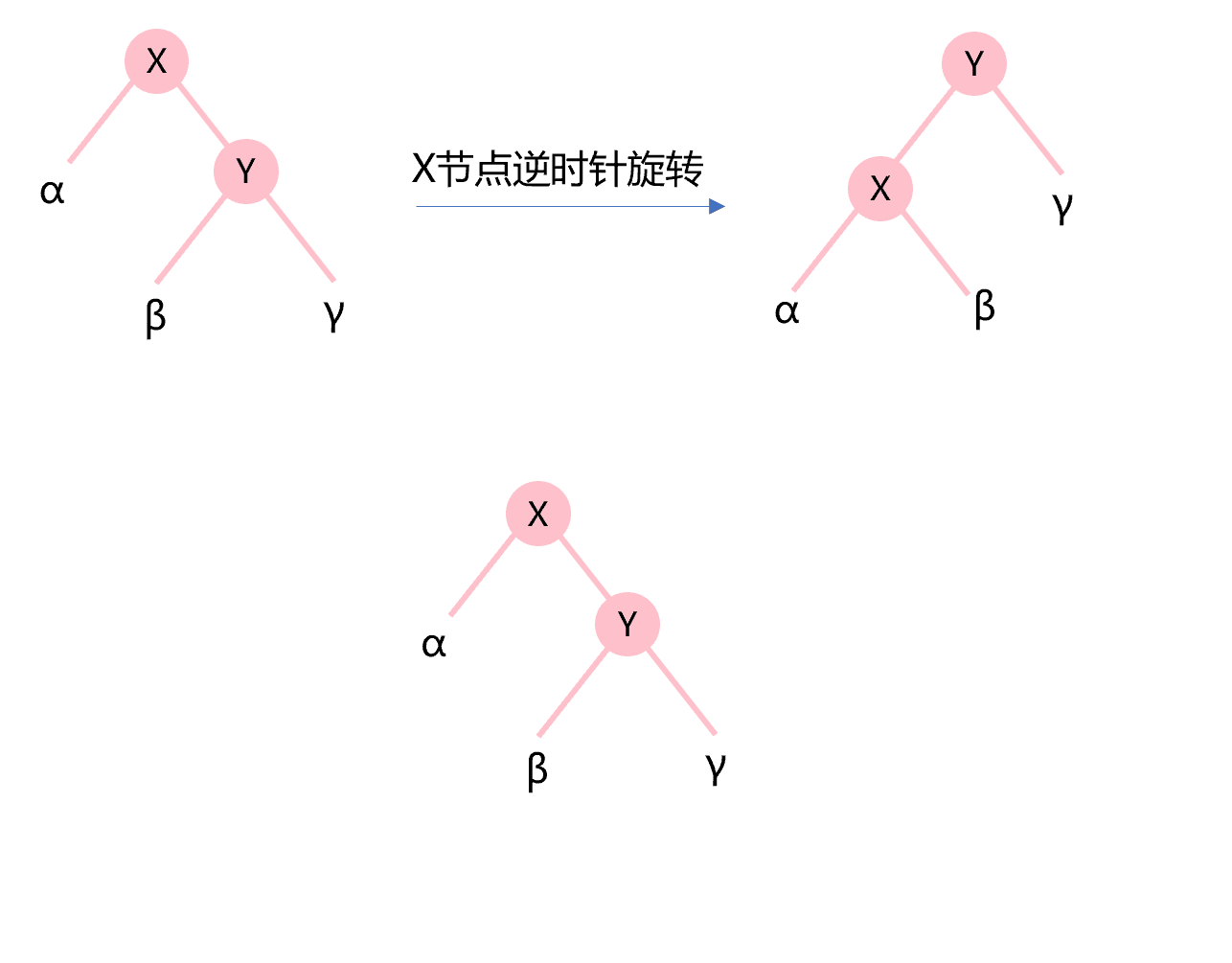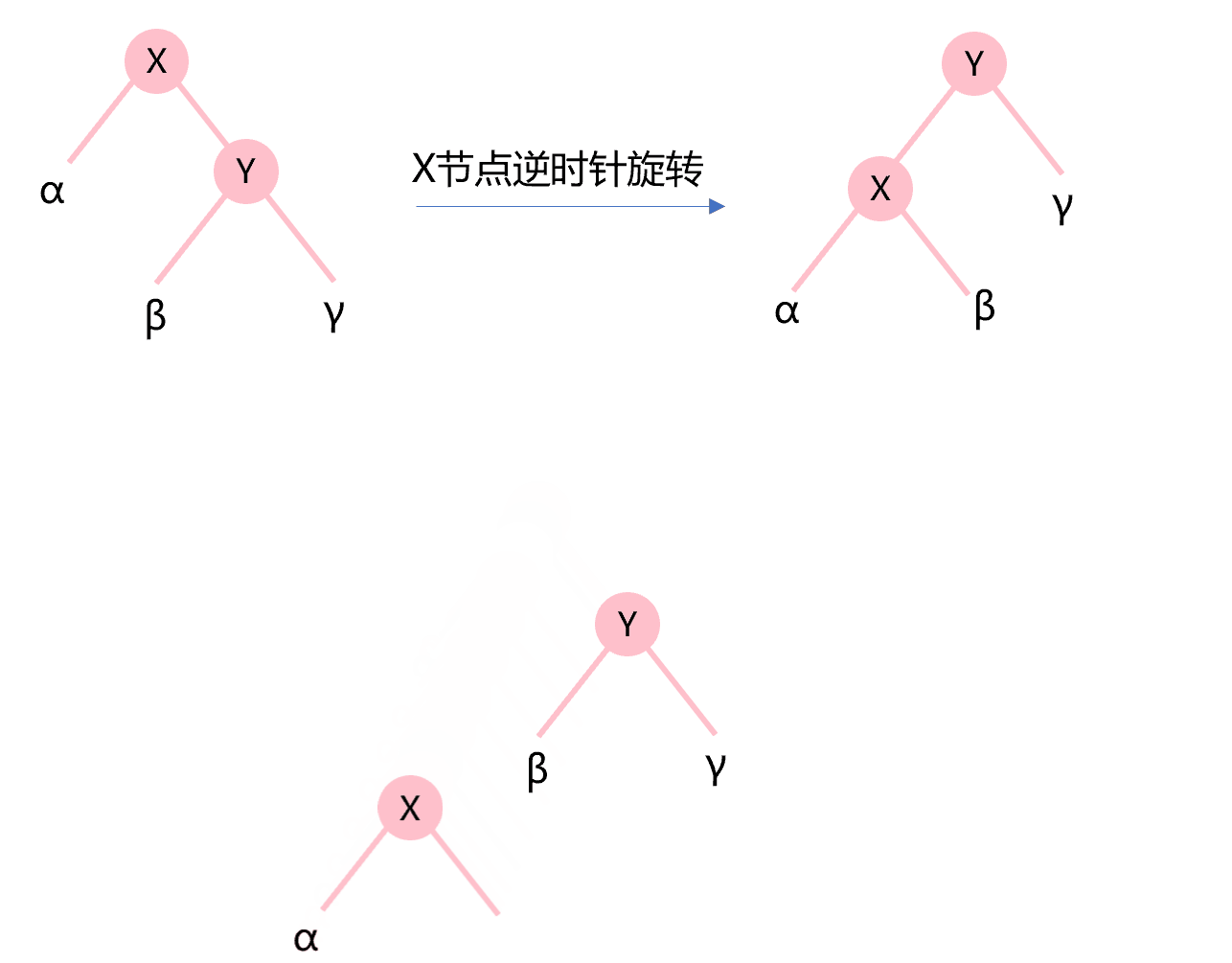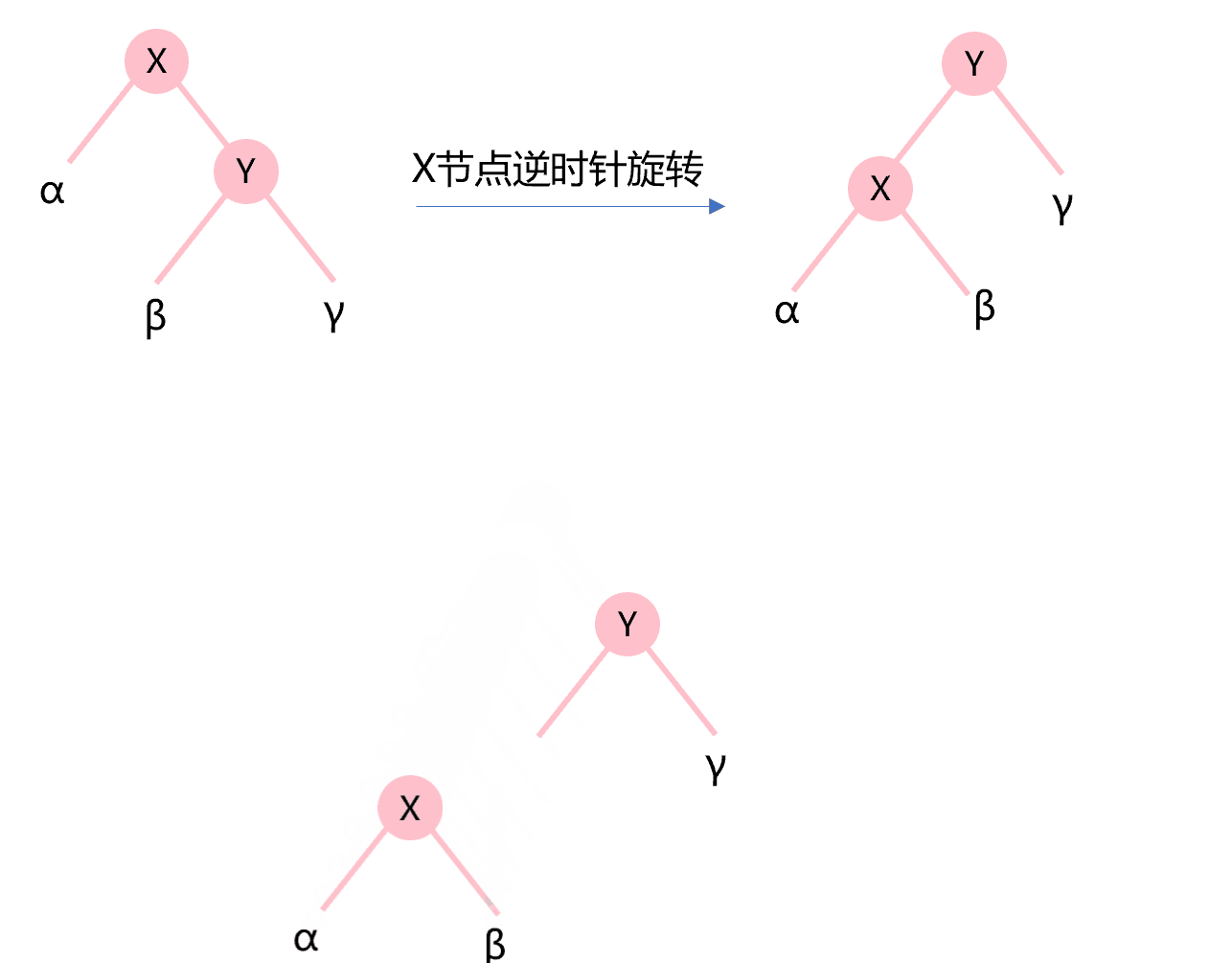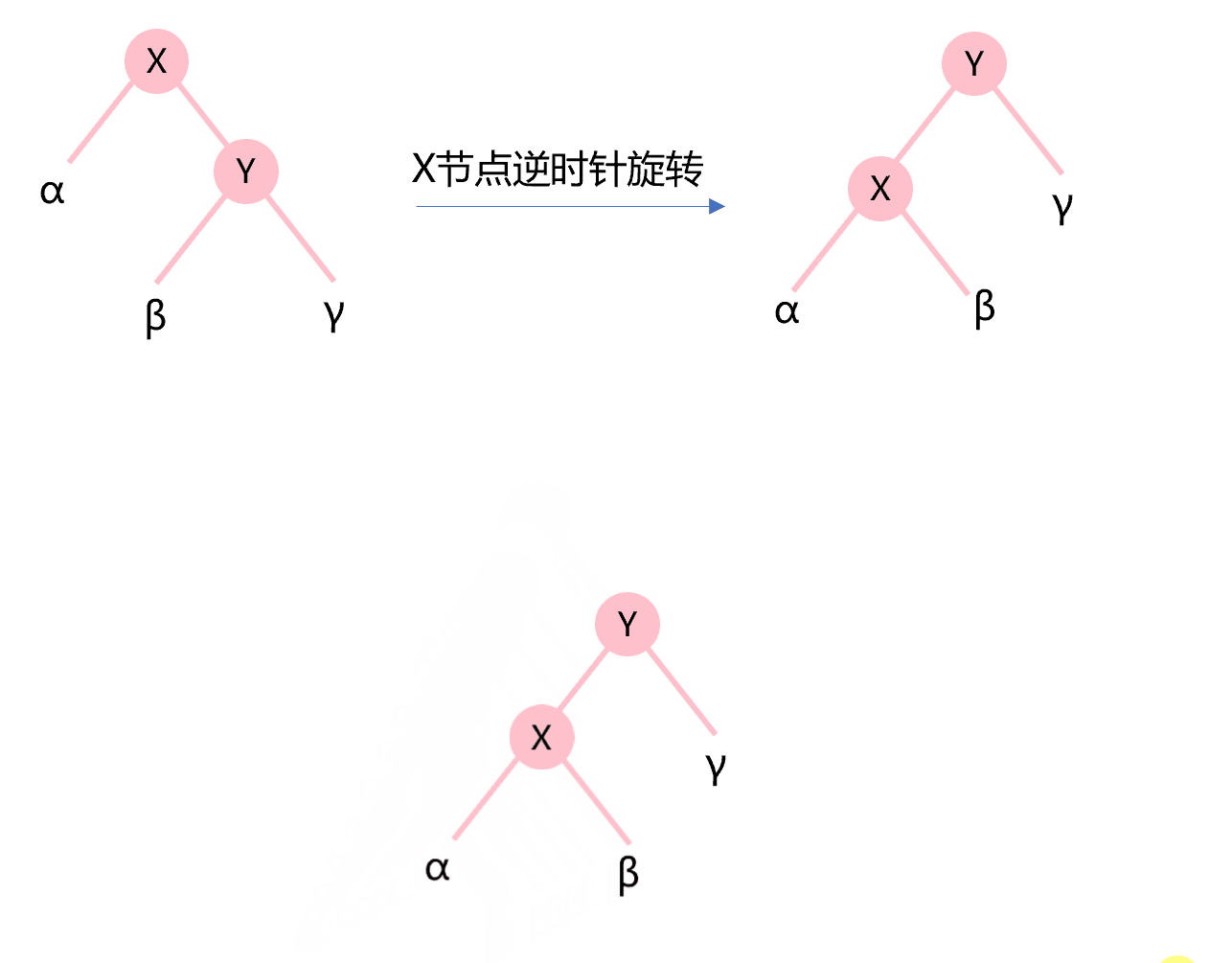
图4.5 节点的逆时针旋转示意图

def rotateCCW(self,node:AVLnode):
        right=node.right
        node.right=right.left
        right.left=node
        node.height=1+max(self.height(node.left),self.height(node.right))
        right.height=1+max(self.height(right.left),self.height(right.right))
        return right
rotateCCW

掌握了节点的顺逆时针旋转后，用一个例子来说明下平衡二叉树的节点插入涉及到的四种情况下的旋转问题。

1.向一棵空树中依次插入H,I,J节点：插入H和J节点并没有破坏高度平衡性，然而继续插入J节点后，BF(H)=-2。J节点插入的位置是H节点右子树的右子树，即RR。这时要将H节点逆时针旋转。

 

2.继续插入B,A节点：插入B节点没有破坏高度平衡性，但是A节点的插入使得BF(H)=2。A节点插入的位置是H节点的左子树的左子树，即LL。这时要将H节点顺时针旋转。

3.插入E节点：插入E节点后，BF(I)=2。E节点插入的位置是I节点的左子树(B)的右子树，即LR。这时先逆时针旋转B节点，再顺时针旋转I节点。可以记作LR=RR(B)+LL(I)。

4.依次插入C,F,D节点：插入C,F节点并没有破坏高度平衡性。继续插入D节点后，BF(B)=-2。D节点插入的位置是B的右子树的左子树中，即RL。这时先顺时针旋转B的右子树(即E节点)，再逆时针旋转B节点，可以记作RL=LL(E)+RR(B)。

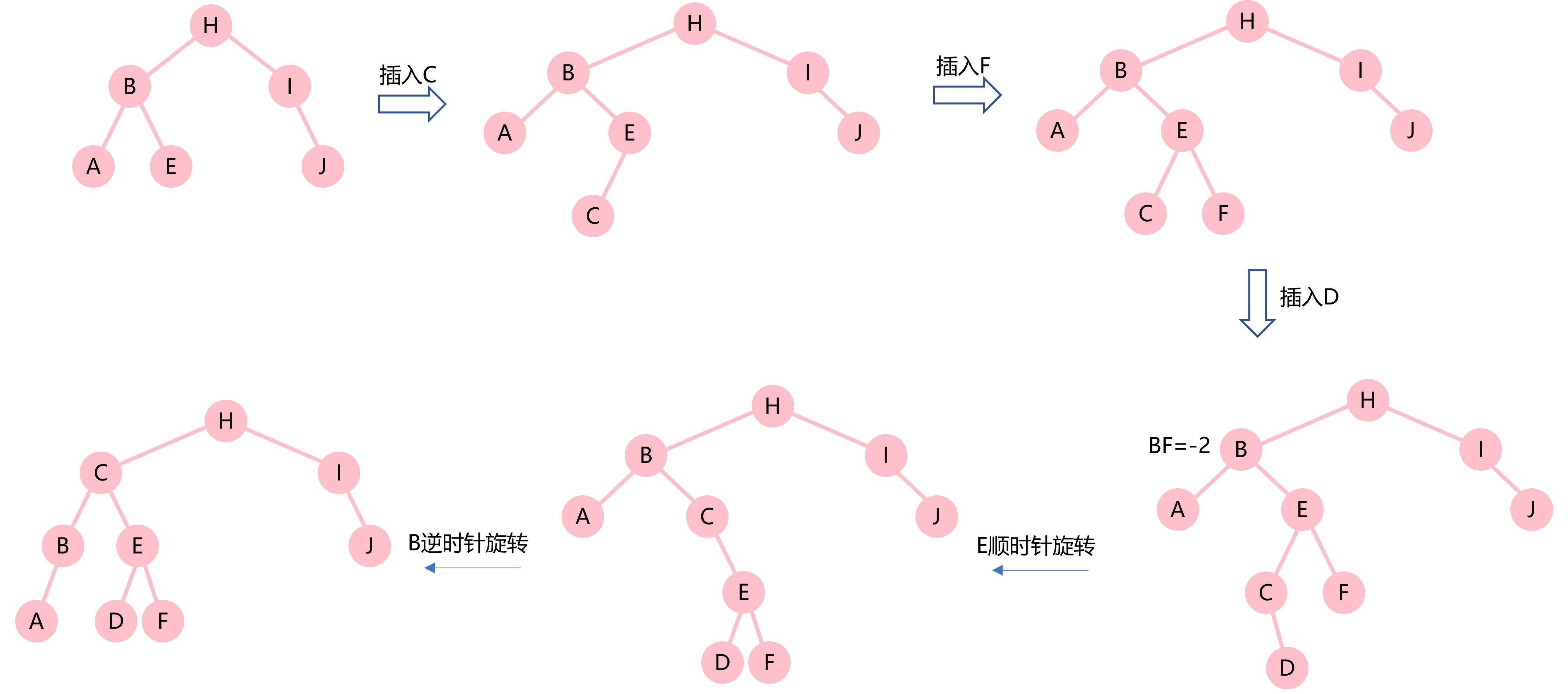
可见，在平衡二叉树中插入节点，首先要确定节点插入的位置，然后再根据其插入后引起的BF的变化决定是否需要旋转以及如何旋转。 

def height(self,node:AVLnode):
        if node:return node.height
        else:return 0
    
    def balanceFactor(self,node:AVLnode):
        if node:
            return self.height(node.left)-self.height(node.right)
        else:return 0
    
    def rotateCW(self,node:AVLnode):
        left=node.left
        node.left=left.right
        left.right=node
        node.height=1+max(self.height(node.left),self.height(node.right))
        left.height=1+max(self.height(left.left),self.height(left.right))
        return left
    
    def rotateCCW(self,node:AVLnode):
        right=node.right
        node.right=right.left
        right.left=node
        node.height=1+max(self.height(node.left),self.height(node.right))
        right.height=1+max(self.height(right.left),self.height(right.right))
        return right
    
    def insert(self,val,root):
        if root is None:return AVLnode(val)
        if val<root.val:
            root.left=self.insert(val,root.left)
        else:
            root.right=self.insert(val,root.right)
        root.height=1+max(self.height(root.left),self.height(root.right))
        BF=self.balanceFactor(root)
        # LL
        if BF>1 and root.left.val>val:
            return self.rotateCW(root)
        # RR
        if BF<-1 and root.right.val<val:
            return self.rotateCCW(root)
        # LR
        if BF>1 and root.left.val<val:
            root.left=self.rotateCCW(root.left)
            return self.rotateCW(root)
        # RL
        if BF<-1 and root.right.val>val:
            root.right=self.rotateCW(root.right)
            return self.rotateCCW(root)
        return root
节点的旋转和插入节点的实现

同样地，删除平衡二叉树中的节点也是先将节点删除，再看是否需要旋转节点。删除节点可分为以下三种情况：

1.删除的是叶子节点，只需要直接删除就可以了。

 

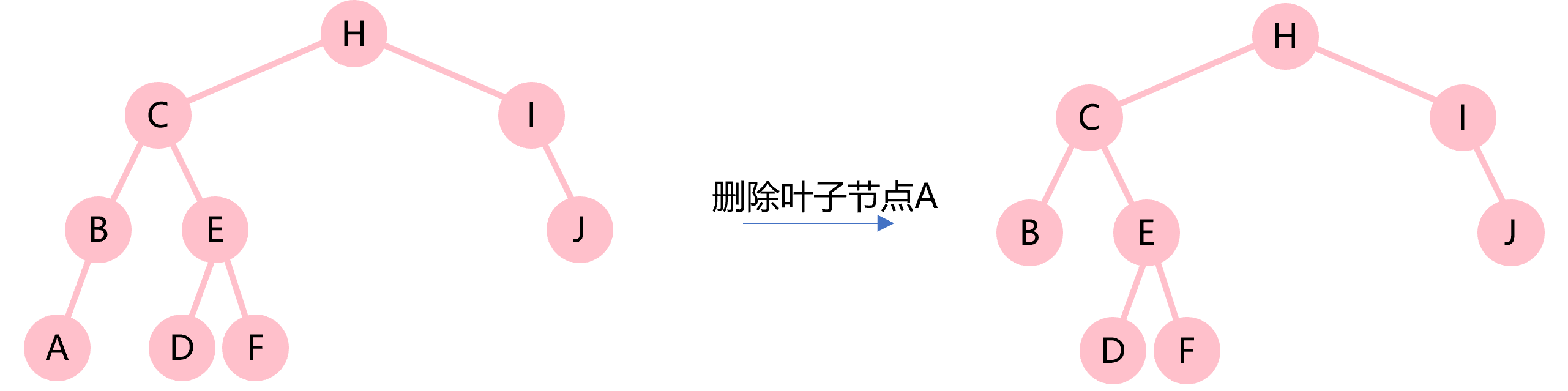
2.删除的节点只有左子树或只有右子树，那么将该节点删除后，它的非空的那棵子树将代替它的位置。

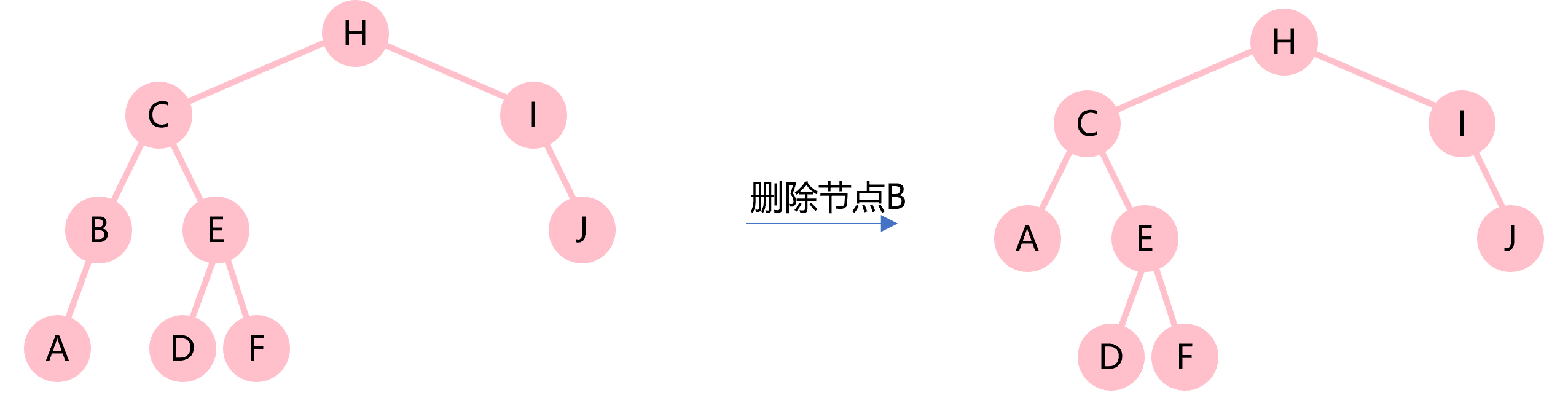
3.删除的节点包含左子树和右子树，那么将该节点删除后，将其右子树中的最左节点作为新的根节点。

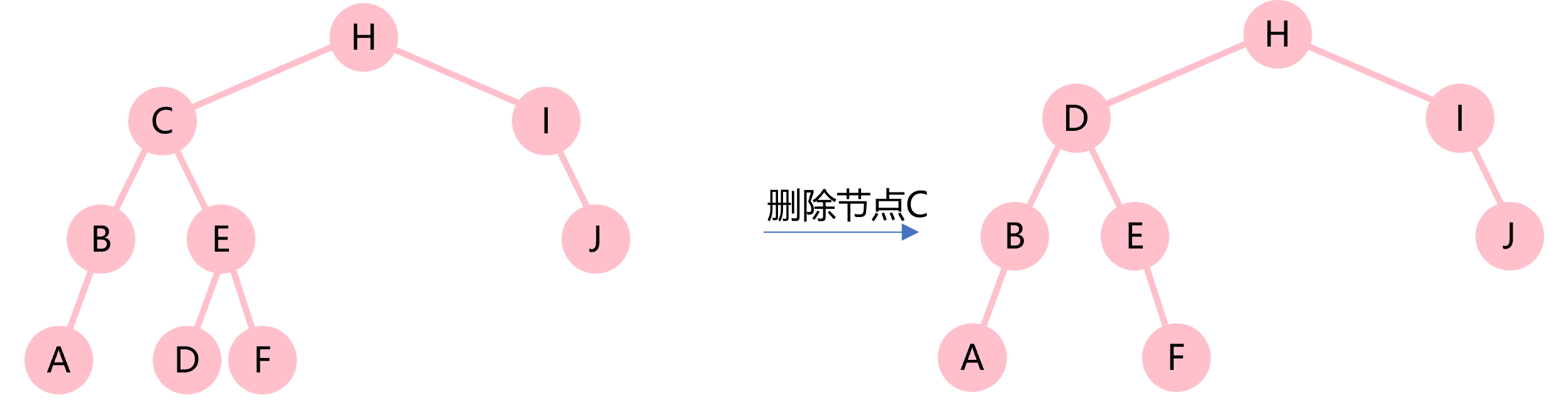
对于删除节点后，引起的高度不平衡的需要节点旋转，分为以下四种情况：

1.BF(node)>1 and BF(node.left)>=0

删除I节点后，BF(H)=2，但是因为H的左子树，即C节点的BF(C)=0，所以只需要顺时针旋转H节点即可。

2.BF(node)>1 and BF(node.left)<0

依次删除A、J节点后，BF(H)=2，且H的左子树BF(C)=-1，此时先逆时针旋转C节点，让BF(C)>=0,这就变成了情况1了，因此只需要再顺时针旋转H节点。

3.BF(node)<-1 and BF(node.right)>0

删除A节点，BF(C)=-2，并且C的右子树BF(H)=1，此时先顺时针旋转H节点，再逆时针旋转C节点。

4.BF(node)<-1 and BF(node.right)<=0

其实就是第三种情况的第二次旋转的部分。

平衡二叉树删除节点的代码如下：

def minimumValueNode(self,node):
        if node is None or node.left is None:
            return node
        else:
            return self.minimumValueNode(node.left)
    
    def delete(self,val,root):
        if root is None:return None
        if val<root.val:
            root.left=self.delete(val,root.left)
        elif val>root.val:
            root.right=self.delete(val,root.right)
        else:
            if root.left is None:
                return root.right
            if root.right is None:
                return root.left
            
            tmp=self.minimumValueNode(root.right)
            root.val=tmp.val
            root.right=self.delete(tmp.val,root.right)
            root.height=1+max(self.height(root.left),self.height(root.right))
            
            BF=self.balanceFactor(root)

            if BF>1 and self.balanceFactor(root.left)>=0:
                return self.rotateCW(root)
            
            if BF>1 and self.balanceFactor(root.left)<0:
                root.left=self.rotateCCW(root.left)
                return self.rotateCW(root)
            
            if BF<-1 and self.balanceFactor(root.right)<=0:
                return self.rotateCCW(root)
            
            if BF<-1 and self.balanceFactor(root.right)>0:
                root.right=self.rotateCW(root.right)
                return self.rotateCCW(root)
            return root
删除平衡二叉树中的节点

4.3.红黑树

这肯定是本篇里面最难的部分了。比起直接给出红黑树的概念和性质，按照《算法》(第4版)所述从2-3树入手理解红黑树我个人感觉比较好。在第1部分提到了2-3树的结构，那么在此基础上，2-3搜索树就是指3节点的左子树的值都小于节点的左边的值，中间子树的值位于左边的值和右边的值之间，右子树的值都大于右边的值，如图1.2所示。

一棵完美平衡的2-3搜索树中的所有null节点到根节点之间的距离都是相同的。为了让2-3树在插入节点时能保持平衡，2-3树的插入规则如下：

1.插入的位置在2节点上，则将该2节点变成3节点即可

2.插入的位置在3节点上

  • 2.1 该3节点就是根节点

　　

  • 2.2 该3节点的根节点为2节点

　　

  • 2.3 该3节点的根节点为3节点

　　   与上面的类似，就是不断地将4节点向上分解，直到遇到一个2节点或者将根分解，使树的高度增高一层。

　　  

对比平衡二叉树的插入和2-3树的插入可以发现，平衡二叉树是由上向下生长的，而2-3树是由下向上生长的。这使得2-3树在最坏的情况下仍有较好的性能。例如，含有10亿个节点的一棵2-3树的高度仅在19-30之间。最多只需要访问30个节点就能够在10亿个值中进行任意查找和插入操作。

红黑树就是用标准的二叉搜索树（完全由2节点构成）和一些额外的信息（表示3节点）的树。顾名思义，额外的信息就是颜色。将3节点表示为两个2节点，其中一个2节点是另外一个的左子树，它的颜色为红，如图4.6所示。

 

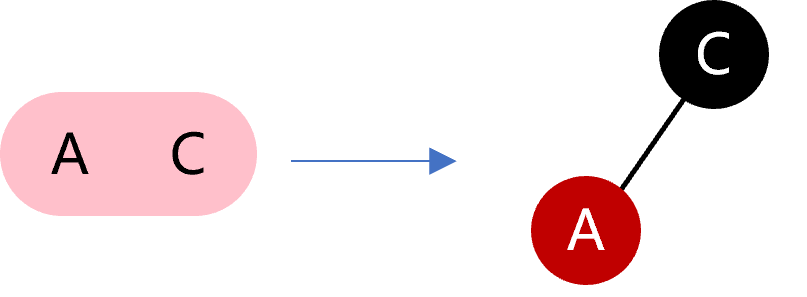
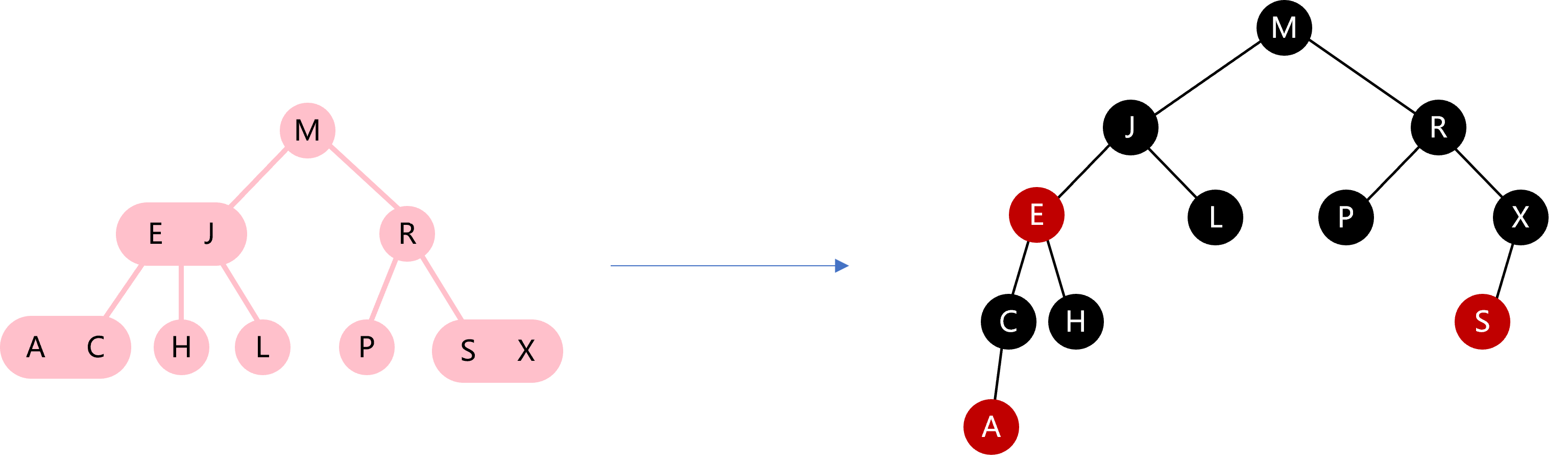
图4.6 3节点表示为两个连接的2节点
class RBTnode:
    def __init__(self,val,n,left=None,right=None,color=1):
        self.val=val
        self.left=left
        self.right=right
        self.color=1 # 1 represents red, 0 represents black
        self.n=n  # 子树中节点的总数
RBT class

 在2-3树作为铺垫的基础上，来看下网络上给出的红黑树的一般定义：

1.根节点是黑色的。

2.红色节点的子节点是黑色的，这里需要注意的是，叶子节点有两个黑色的null子节点。

3.从根节点到每一个null节点的路径上所包含的黑色节点的数量是相同的。

是不是就能够理解了。反正我一开始光看上面这个定义，根本不明白为什么红黑树要这样定义。

红黑树插入新节点的特点是，都先默认插入的是红色的节点，然后再通过旋转或者改变颜色使其满足红黑树的定义。因此，红黑树的旋转如下：

图4.7 红黑树的顺时针旋转
图中绿色节点的意思是这个节点可能是红色的也可能是黑色的。
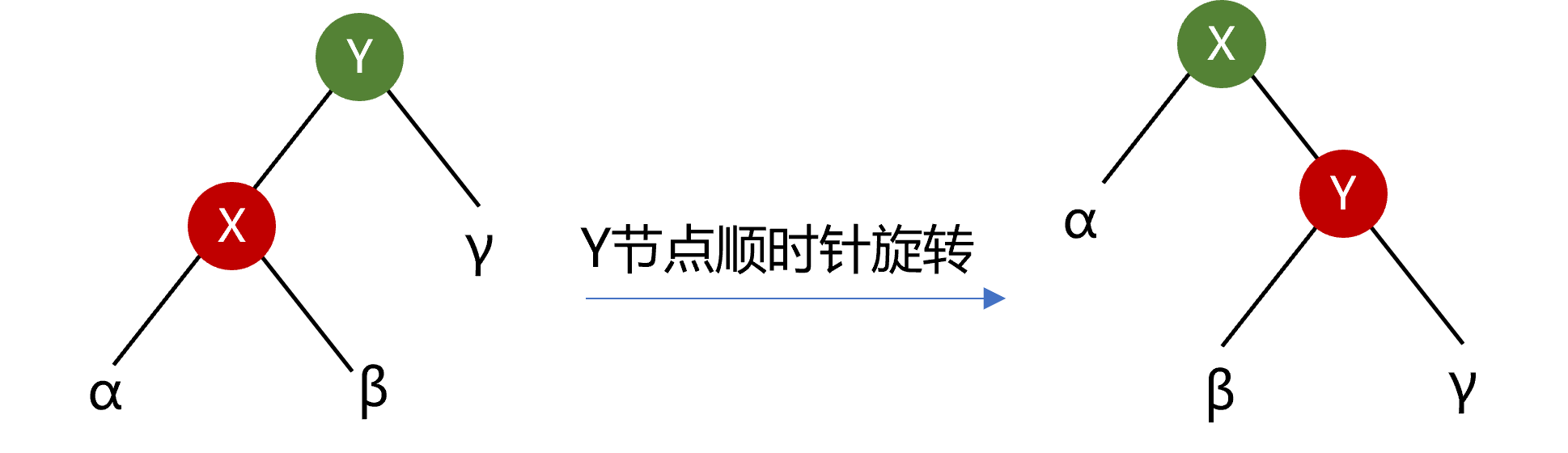
def rotateCW(self,node:RBTnode):
        left=node.left
        node.left=left.right
        left.right=node
        left.color=node.color
        node.color=1
        left.n=node.n
        node.n=1+self.size(node.left)+self.size(node.right)
        return left
rotateCW

 

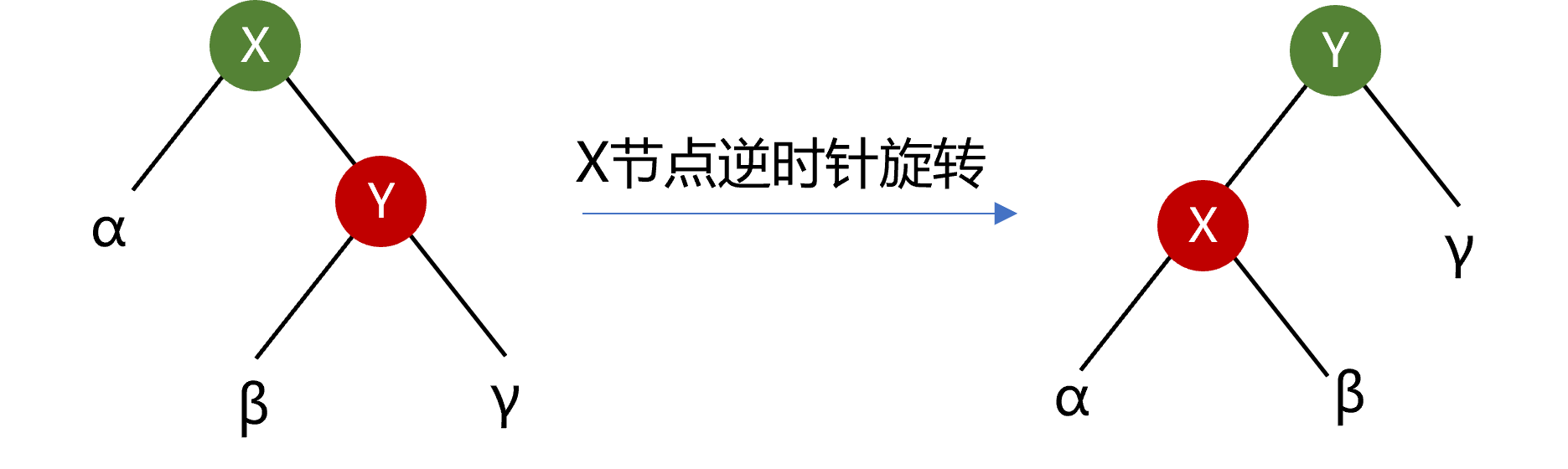
图4.8 红黑树的逆时针旋转

def rotateCCW(self,node:RBTnode):
        right=node.right
        node.right=right.left
        right.left=node
        right.color=node.color
        node.color=1
        right.n=node.n
        node.n=1+self.size(node.left)+self.size(node.right)
        return right
rotateCCW

除了旋转外，红黑树还有一个操作就是改变颜色，即把红色节点变成黑色节点。插入节点的过程可以分为三种情况：

1.如果右子节点是红色的而左子节点是黑色的，则进行逆时针旋转

2.如果左子节点是红色的，且左子节点的左子节点也是红色的，则进行顺时针旋转

3.如果左右子节点均是红色的，则将它们俩变成黑色的

因此，红黑树插入新节点的代码如下：

def insert(self,val,root):
        if root is None:
            root=RBTnode(val)
        else:
            if val<root.val:
                root.left=self.insert(val,root.left)
            else:
                root.right=self.insert(val,root.right)
            if self.isRed(root.right) and not self.isRed(root.left):
                root=self.rotateCCW(root)
            if self.isRed(root.left) and self.isRed(root.left.left):
                root=self.rotateCW(root)
            if self.isRed(root.left) and self.isRed(root.right):
                root.color=1
                root.left.color=0
                root.right.color=0
            root.n=self.size(root.left)+self.size(root.right)+1
        root.color=0
        return root
RBT insert

（红黑树删除节点部分未完待续）

红黑树的应用：Java的HashMap实现，Linux CFS调度程序 

4.4.线段树

来看下leetcode307题，对于一个整数数组nums，实现NumArray类：

  • NumArray(int[] nums)  用整数数组nums初始化对象
  • void update(int index, int val)  将nums[index]的值更新为val
  • int sumRange(int left, int right)  返回数组nums种索引left和索引right(包括left和right)之间的nums元素的和

乍一看非常简单，update()就是根据索引查找，然后更新数组，sumRange就是计算和而已。当时我还想就这还能是中等难度，自以为是的轻轻松松把代码写出来提交，结果超时了。问题肯定是出在求区间和上，因为针对每个给定的区间[start,end]，都要逐一计算区间内所有元素的和。如果在初始化数组的时候就计算出相应的区间和的话，那么sumRange函数就可以转换为查询问题了。针对这类问题，线段树就派上了用场。

线段树(segment tree)在数据结构上属于一棵完全二叉树，通过利用“二分”的优势高效地解决数组中的区间问题（包括区间求和、最值等），同时也允许灵活地更改数组。以区间求和为例，对于给定的一个整数数组nums，求[start,end]区间上的和，可以分别求左区间、右区间的和，再相加。即

Sum([start,end])=Sum([start,mid])+Sum([mid+1,end])

不断地递归算下去的，直到start==end，这时Sum[start,end]=nums[start]。对于下面这个数组：

nums=[1,3,-2,8,-7]，则有

  • Sum([0,4])=Sum([0,2])+Sum([3,4])
  • Sum([0,2])=Sum([0,1])+Sum([2,2])=Sum([0,0])+Sum([1,1])+nums[2]=nums[0]+nums[1]+nums[2]
  • Sum([3,4])=Sum([3,3])+Sum([4,4])=nums[3]+nums[4]

用完全二叉树表示则如图4.9所示，其中非叶子节点的值等于其左子节点值和右子节点值的和，叶子节点的值对应着整数数组中的值。

 

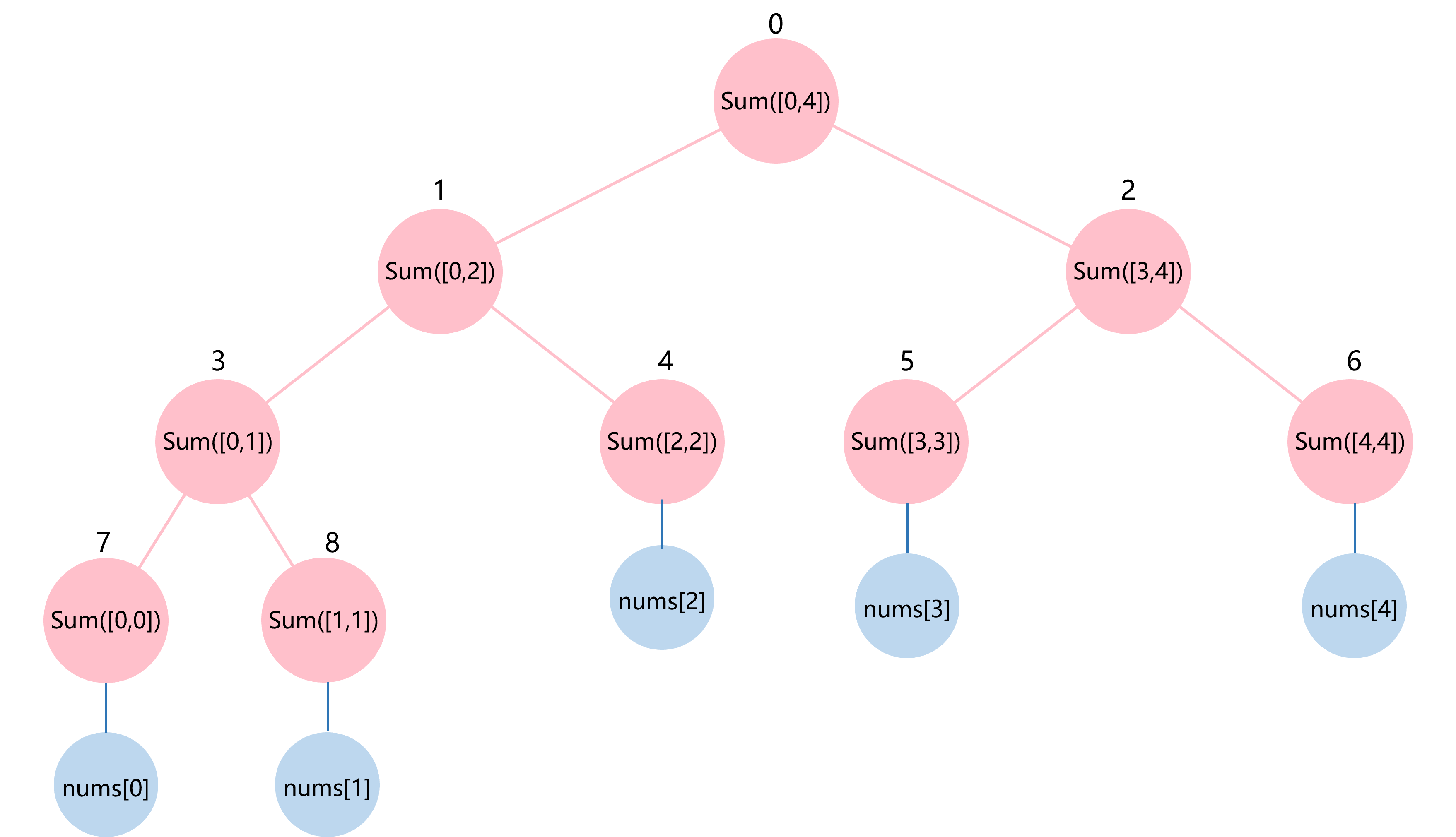
图4.9 线段树

根据第2部分内容可知，这棵完全二叉树可以用数组表示，这里将数组命名为segmentTree。在初始化NumArray类时，就是要构建segmentTree数组。首先确定segmentTree的长度。根据第2部分的内容可知，一棵高度为h的二叉树在第i层上的节点数最多为2^i个，整棵树的节点最多有2^h-1个。令n=len(nums)，则有：

也就是说这棵求和的线段树的高度h满足：

 

那么这棵二叉树的segmentTree数组的长度L满足：

即对于长度为n的整数数组，其对应的线段树的数组的长度不会超过4n。构建segmentTree数组是一个递归的过程，代码如下：

class NumArray:
    def __init__(self,nums):
        self.l=len(nums)
        self.segmentTree=[0]*(4*self.l)
        def build(i,s,e):
            if s==e:
                self.segmentTree[i]=nums[s]
            else:
                mid=s+(e-s)//2
                build(2*i+1,s,mid)
                build(2*i+2,mid+1,e)
                self.segmentTree[i]=self.segmentTree[2*i+1]+self.segmentTree[2*i+2]
        build(0,0,self.l-1)
initiate NumArray

有了segmentTree数组后，计算给定的区间[start,end]的区间和的问题可以通过遍历线段树实现：

  • 如果[start,end]在当前区间的左子区间内，即end<mid，则遍历其左子树
  • 如果[start,end]在当前区间的右子区间内，即start>=mid，则遍历其右子树
  • 如果[start,end]刚好对应当前区间，则直接返回该节点的值
  • 如果[start,end]与当前区间交叉但不重合，则返回[start,mid]+[mid+1,end]的值

代码如下：

def sumRange(self,left,right):
        def range(left,right,i,s,e):
            if s==left and e==right:
                return self.segmentTree[i]
            else:
                mid=s+(e-s)//2
                if left>mid:
                    return range(left,right,2*i+2,mid+1,e)
                if right<=mid:
                    return range(left,right,2*i+1,s,mid)
                return range(left,mid,2*i+1,s,mid)+range(mid+1,right,2*i+2,mid+1,e)
        range(left,right,0,0,self.l-1)
sumRange

 更新线段树的代码如下：

def update(self,index,val):
        def change(i,s,e):
            if s==e:
                self.segmentTree[i]=val
            else:
                mid=s+(e-s)//2
                if index<=mid:
                    change(2*i+1,s,mid)
                else:
                    change(2*i+2,mid+1,e)
                self.segmentTree[i]=self.segmentTree[2*i+1]+self.segmentTree[2*i+2]
        change(0,0,self.l-1)
update

4.5.堆

本质上，堆是一棵完全二叉树。根据根节点和子节点的大小，可以分为（如图4.10所示）：

  • 大根堆(max heap)，根节点大于所有的子节点
  • 小根堆(min heap)，根节点小于所有的子节点
       

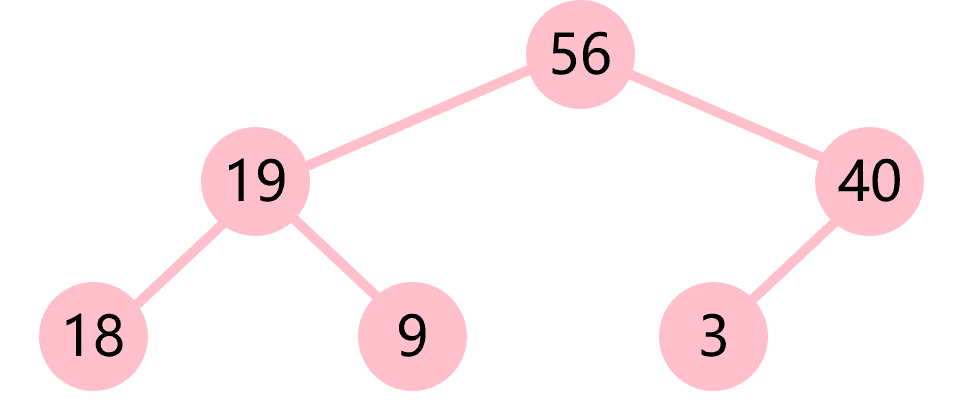
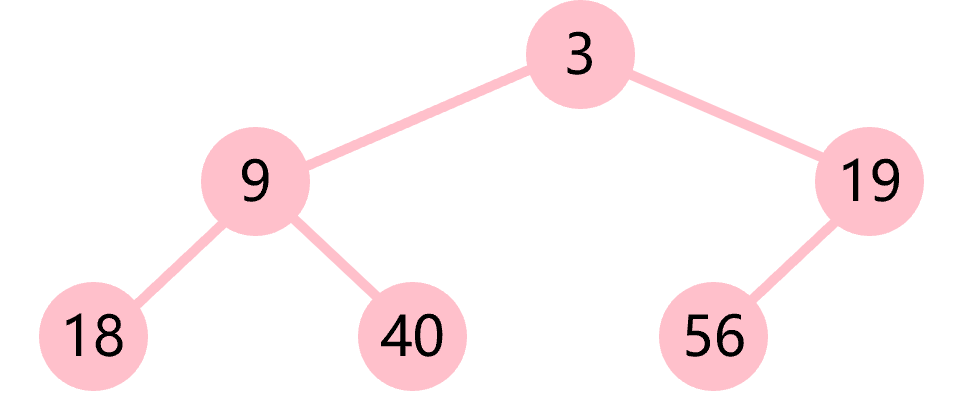
a)大根堆                                           b)小根堆

图4.10 堆

在完全二叉树部分提到，二叉树可以表示为一维数组，索引为i的根节点的两个子节点的索引分别为2i+1和2i+2。那么就可以给出堆的定义：

n个元素的序列[K0, K1,...,Ki,..., Kn-1]当且仅当满足：
 
 为小根堆
 
为大根堆

以图23 a)所示的大根堆为例，可以表示为如下数组：[56,19,40,18,9,3]。向该大根堆中插入45的步骤如下：

1.先将45插入到数组尾部，此时45的索引为6，则其父节点的索引为（6-1）//2=2，即45的父节点为40。

2.比较40和45，45大于40，因此需要交换这两个节点，得到的新数组为[56,19,45,18,9,3,40]。此时45的索引为2，其父节点的索引为0。即当前45的父节点为56。

3.45<56，满足大根堆的定义，无需交换，插入新值完成。

删除堆顶元素的步骤如下：

1.将数组尾部的元素与首元素交换，得到的新数组为[3,19,40,18,9,56]。

2.将56删除，剩下的元素重新堆化，即将堆顶元素不断与其子节点比较-交换，得到新数组[45,19,3,18,9]。

可见，不断地删除堆顶元素，就可以实现数组的排序。堆支持动态插入和删除，时间复杂度为O(logn)，查询最值得时间复杂度为O(1)，排序的时间复杂度为O(nlogn)。因此堆常用于解决Kth最值问题，这里随便贴上两道题。

leetcode215,数组中的第K个最大元素：给定整数数组nums和整数k，请返回数组中第k个最大的元素。示例：

[3,2,1,5,6,4]，k=2，则返回5.

当然，使用堆并不是这道题唯一的做法，也可以先排序，快速排序，冒泡都可以啊，当然也可以使用堆排序。这里给出的是python代码，因为python里面的堆默认是小根堆，因此遇到这种求第k个最大元素的，可以先把元素都变成负数。

class Solution:
    def findKthLargest(self, nums: List[int], k: int) -> int:
        import heapq
        maxHeap=[]
        for i in nums:
            heapq.heappush(maxHeap,-i)
        for i in range(k-1):
            heapq.heappop(maxHeap)
        return -maxHeap[0]
Kth largest

leetcode347. 给一个整数数组nums和一个整数k，请返回其中出现频率前k高的元素，可以按任意顺序返回答案。示例：

nums=[1,1,1,2,2,3], k=2，返回[1,2]。

思路：先用字典记录元素出现的个数，然后按照出现个数排序，返回前k高的就可以了。python代码如下：

class Solution:
    def topKFrequent(self, nums: List[int], k: int) -> List[int]:
        dict1={}
        for i in nums:
            if i in dict1.keys():
                dict1[i]+=1
            else:
                dict1[i]=1
        import heapq
        vals=[]
        for i in dict1.keys():
            if len(vals)<k:
                heapq.heappush(vals,(dict1[i],i))
            else:
                top=vals[0]
                if top[0]<dict1[i]:
                    heapq.heappushpop(vals,(dict1[i],i))
        ans=[]
        for i in vals:
            ans.append(i[1])
        return ans
topKFrequent

5.参考文献

AVL Trees using Python (chercher.tech)

Red Black Tree - javatpoint

Segment Tree - Algorithms for Competitive Programming (cp-algorithms.com)

算法（第4版）

关于堆的文献当时忘记记录了，应该也是博客园上的某些博客

posted @ 2022-05-23 20:26  南风小斯  阅读(579)  评论(0)  编辑  收藏  举报